5 Key Answers for Special Right Triangles Worksheet

Understanding special right triangles can significantly simplify solving geometric problems, especially in trigonometry and algebra. These triangles have specific angle measurements and side ratios that make calculations much easier. Here are five key answers you'll find useful when working through a worksheet on special right triangles:
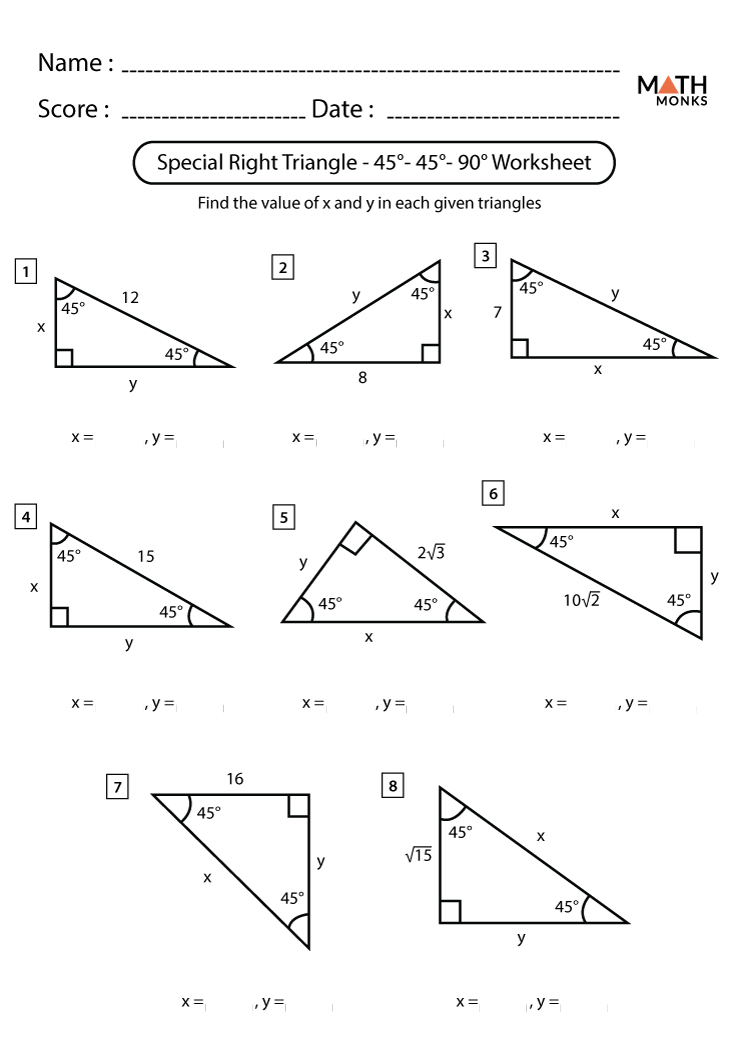
1. 45-45-90 Triangles

These triangles are isosceles, with two sides equal in length, and one 90-degree angle. Here’s what you need to know:
- Hypotenuse to Leg Ratio: The ratio of the hypotenuse to one of the legs is 1:√2. This means if each leg is x, the hypotenuse will be x√2.
- Legs Relationship: In a 45-45-90 triangle, both legs are congruent, making it particularly easy to find missing sides.
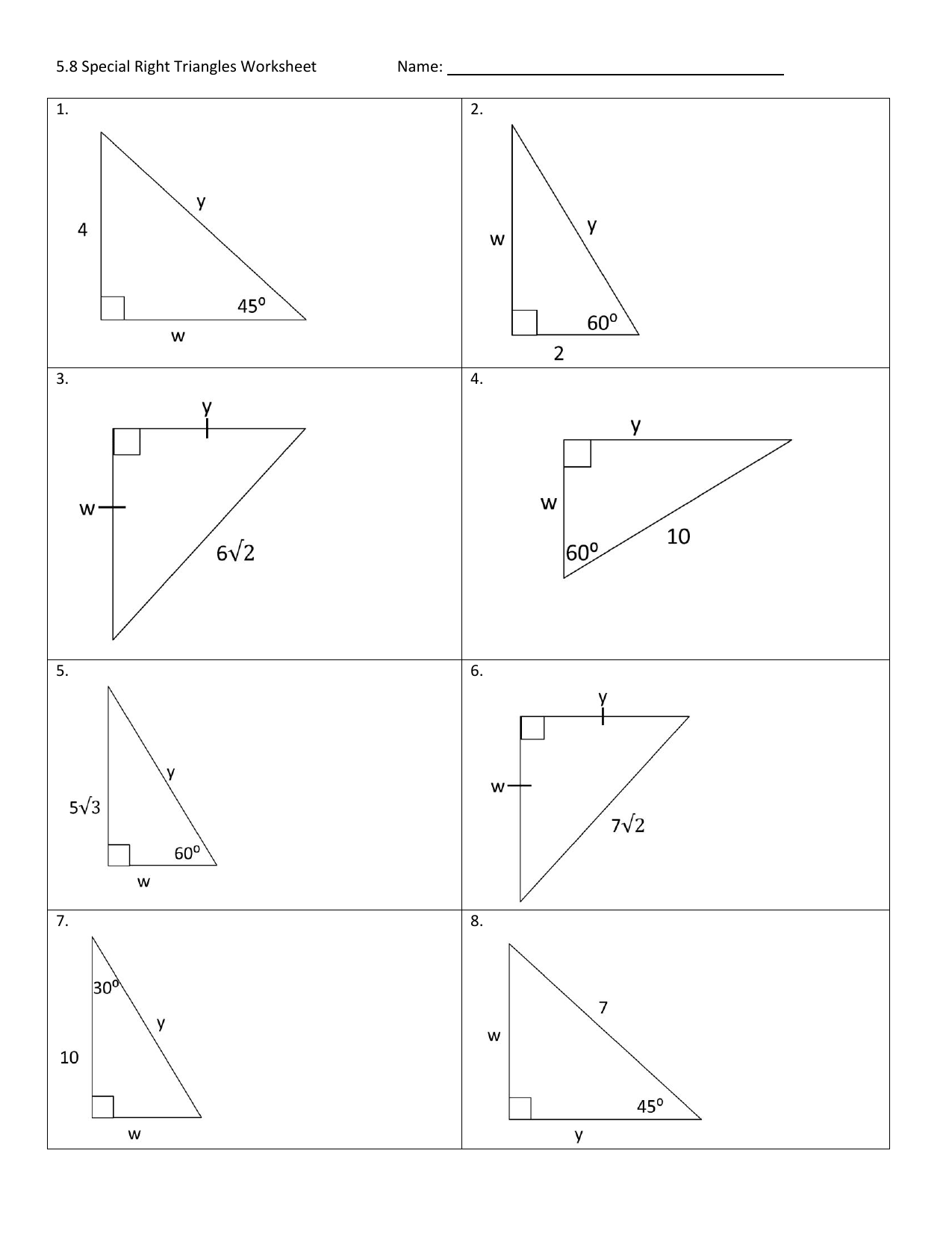
2. 30-60-90 Triangles
This triangle features one 90-degree angle and sides in the ratio 1:√3:2:
- Short Leg: If the shortest side (opposite the 30-degree angle) is x, the hypotenuse will be 2x.
- Longer Leg: The side opposite the 60-degree angle is x√3.
3. Using Trigonometric Ratios

For special right triangles, you can use trigonometric functions to find unknown sides or angles:
- Sine, Cosine, and Tangent: These functions are simplified in these triangles. For example:
- In a 45-45-90 triangle, sin(45°) = cos(45°) = 1/√2 or √2/2.
- In a 30-60-90 triangle, sin(30°) = 1⁄2, sin(60°) = √3/2, cos(30°) = √3/2, and cos(60°) = 1⁄2.
4. Pythagorean Theorem in Special Triangles

While not as straightforward as ratios, here’s how the Pythagorean theorem applies:
| Type of Triangle | Hypotenuse | Leg 1 | Leg 2 |
|---|---|---|---|
| 45-45-90 | x√2 | x | x |
| 30-60-90 | 2x | x | x√3 |

🔍 Note: Always remember that the Pythagorean theorem confirms these ratios but isn't necessary for direct calculations.
5. Visualizing Special Right Triangles

Understanding the geometry through visualization can enhance your problem-solving:
- 45-45-90 Triangle: Think of folding a square in half diagonally; you get two 45-45-90 triangles.
- 30-60-90 Triangle: Start with an equilateral triangle and bisect one of its angles; you create two 30-60-90 triangles.
In conclusion, mastering special right triangles involves memorizing their unique ratios, understanding how trigonometric functions apply, and recognizing the geometric constructions that form these triangles. By internalizing these concepts, you not only become adept at solving related problems but also enhance your overall geometric reasoning and problem-solving skills.
What makes a 45-45-90 triangle special?
+
The 45-45-90 triangle is special because it has two equal angles of 45 degrees and a hypotenuse that is √2 times the length of each leg. This relationship simplifies many calculations in geometry and trigonometry.
How do I know if I should use a 30-60-90 triangle for a problem?

+
You should use a 30-60-90 triangle when one of the angles is 30 or 60 degrees, or if the problem involves an equilateral triangle that has been split into two right triangles.
Can I apply these ratios to any triangle?

+
No, these ratios specifically apply to the 45-45-90 and 30-60-90 right triangles. For other triangles, you’ll need to use other methods or the general Pythagorean theorem.