30-60-90 Triangle Secrets: 5 Key Worksheet Tips
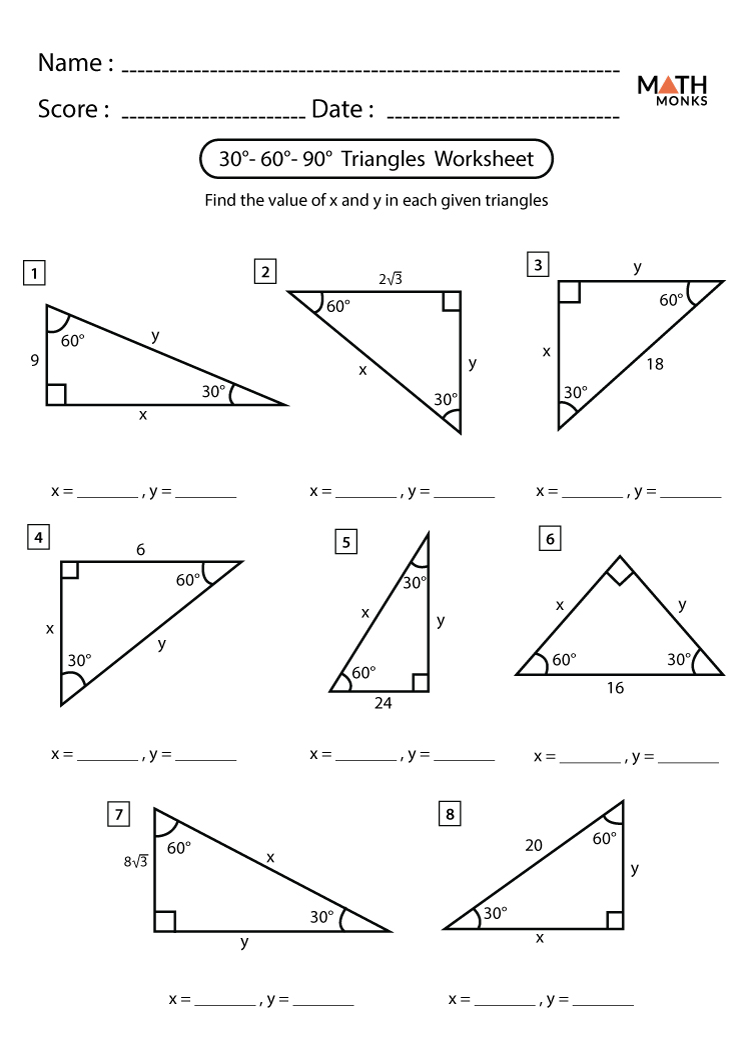
Exploring the intricacies of 30-60-90 triangles can unlock a multitude of mathematical understandings, especially in geometry and trigonometry. These unique triangles have specific properties that can simplify problem-solving and enrich your mathematical toolkit. Here are five key worksheet tips to master 30-60-90 triangles:
Understanding the Basics

Before diving into the complexities, ensure you have a firm grasp of the basic properties:
- The angles are always 30°, 60°, and 90°.
- The sides are in a specific ratio:
- Shortest side (opposite the 30° angle) = x
- Medium side (opposite the 60° angle) = x√3
- Longest side (hypotenuse, opposite the 90° angle) = 2x
Worksheet Tip 1: Visualize and Identify

Use visual aids to instantly recognize 30-60-90 triangles:
- Sketch a 30-60-90 triangle every time you encounter one in a problem or worksheet. This visualization helps in internalizing the angle relationships and side ratios.
- Highlight or mark the angles directly on the worksheet for quick reference during calculations.
Remember, when the triangle is not explicitly labeled as 30-60-90, identify it through its properties like:
- An isosceles right triangle split in half at the right angle.
- One angle is 30°, another 60°, and the third must be 90°.
Worksheet Tip 2: Ratios and Relationships

Leverage the ratios to simplify calculations:
- Recognize that if you know one side, you can find the other two using the ratios: x, x√3, and 2x.
- Use these ratios for quick calculations, especially in trigonometry problems where sine, cosine, and tangent values for these angles are straightforward.
| Angle | Side Opposite | Side Adjacent to 90° | Length Relative to Shortest Side (x) |
|---|---|---|---|
| 30° | x | 2x | x |
| 60° | x√3 | 2x | x√3 |
| 90° | 2x | - | 2x |

📌 Note: Remember, the ratios simplify trigonometric function values for these angles; sin(30°) = 1⁄2, cos(60°) = 1⁄2, and tan(30°) = √3/3.
Worksheet Tip 3: Trigonometric Values

Know and use trigonometric values directly:
- Sine, cosine, and tangent for 30° and 60° are derived from the ratios of the sides:
- sin(30°) = 1⁄2, cos(30°) = √3/2, tan(30°) = √3/3
- sin(60°) = √3/2, cos(60°) = 1⁄2, tan(60°) = √3
- These values help in solving problems involving angular relationships and side lengths, even when the triangle isn’t labeled as 30-60-90.
Worksheet Tip 4: Practical Applications

Apply 30-60-90 triangle knowledge to real-world problems:
- Height problems: The height of an isosceles triangle when split into two 30-60-90 triangles.
- Length measurements: When given angles, estimate distances or lengths in construction, navigation, or engineering problems.
- Trigonometry problems: Solve for unknown sides or angles in complex geometric shapes or scenarios.
Worksheet Tip 5: Mastery through Practice

Practice until 30-60-90 triangles become second nature:
- Regularly solve different types of problems involving 30-60-90 triangles to reinforce your understanding.
- Consider creating your own problems or finding resources online to keep practicing.
As you delve deeper into the mysteries of 30-60-90 triangles, these tips will serve as your compass. Remember, the beauty of mathematics lies in its patterns and the elegance of simplicity. With these strategies, not only will you solve problems with ease, but you'll also appreciate the underlying harmony of geometric shapes. These triangles are not just mathematical constructs; they are a testament to the order and predictability of the universe's design. Keep practicing, and soon, you'll see these triangles everywhere, from simple height calculations to the most intricate design problems.
What is a 30-60-90 triangle?

+
A 30-60-90 triangle is a special type of right-angled triangle where the angles are precisely 30 degrees, 60 degrees, and 90 degrees. The sides have a unique relationship: the side opposite the 30-degree angle is x, the side opposite the 60-degree angle is x√3, and the hypotenuse (opposite the 90-degree angle) is 2x.
Why are 30-60-90 triangles important in mathematics?

+
30-60-90 triangles are crucial because of their predictable ratios, which simplify trigonometric calculations and geometric problem-solving. They appear in various applications, from architecture to physics, due to their regular and understandable properties.
How do I identify a 30-60-90 triangle if it’s not explicitly labeled?

+
Look for:
- An isosceles right triangle split in half at the right angle.
- One angle is 30° and another is 60°, with the third angle must be 90°.
- Side ratios can also help confirm the identity if you know at least one side length.
Related Terms:
- 30 60 90 triangles worksheet answer key
- 45 45 90 triangle worksheet
- 30 60 90 and 45 45 90 triangle worksheet