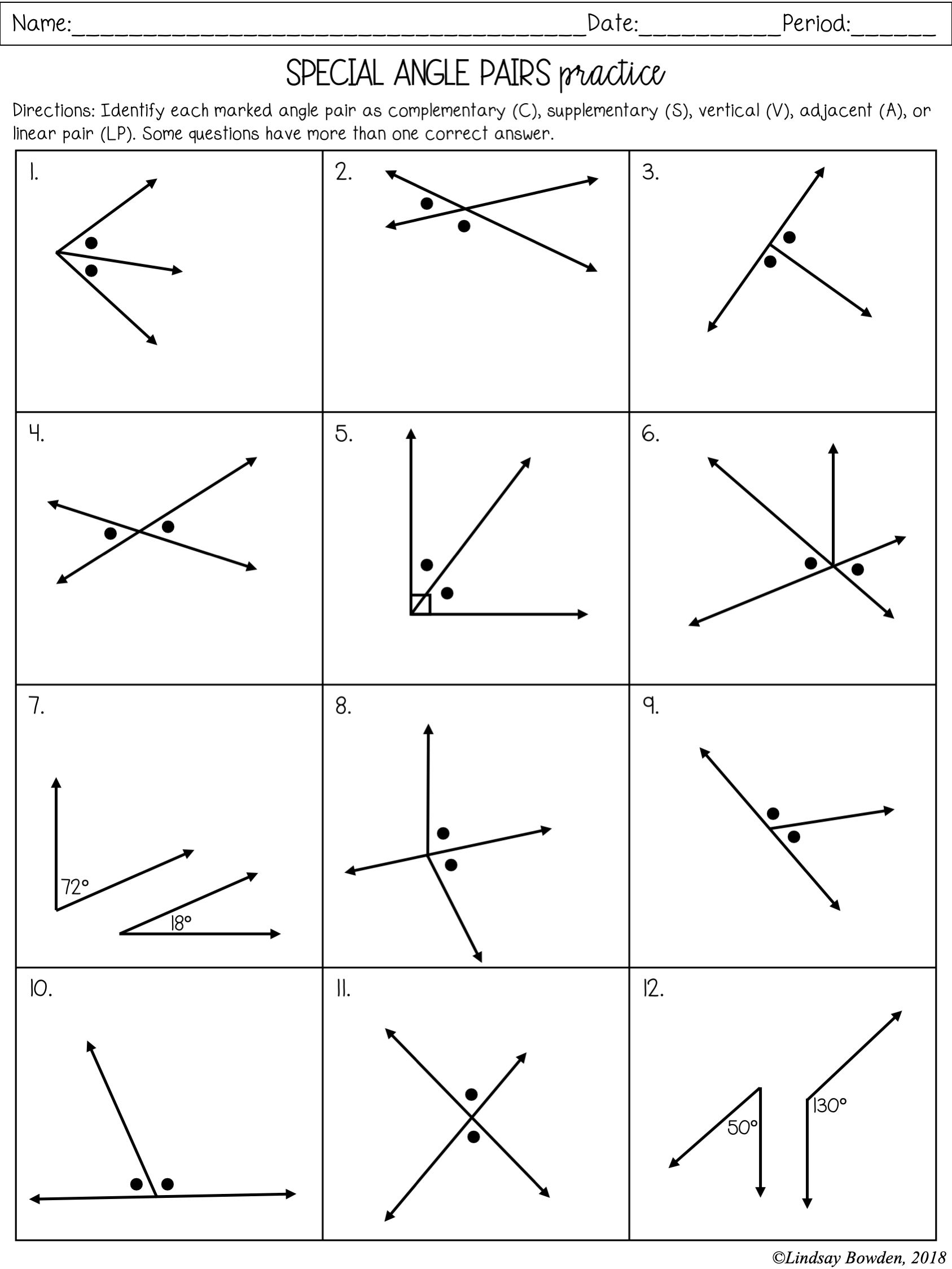
Special Angle Pairs Worksheet: Answer Key Revealed

In the world of geometry, understanding the relationships between angles can significantly enhance one's ability to solve complex problems efficiently. One particularly fascinating aspect of this field involves exploring special angle pairs — those unique sets of angles formed by intersecting lines, parallel lines with a transversal, or within polygons. This blog post unveils an Answer Key for a Special Angle Pairs Worksheet to guide learners in mastering these concepts. We will delve into definitions, provide examples, offer insightful tips, and explore real-world applications of these angles. Whether you are a student, teacher, or math enthusiast, this detailed walkthrough will ensure you grasp how to identify and use these angle pairs effectively.
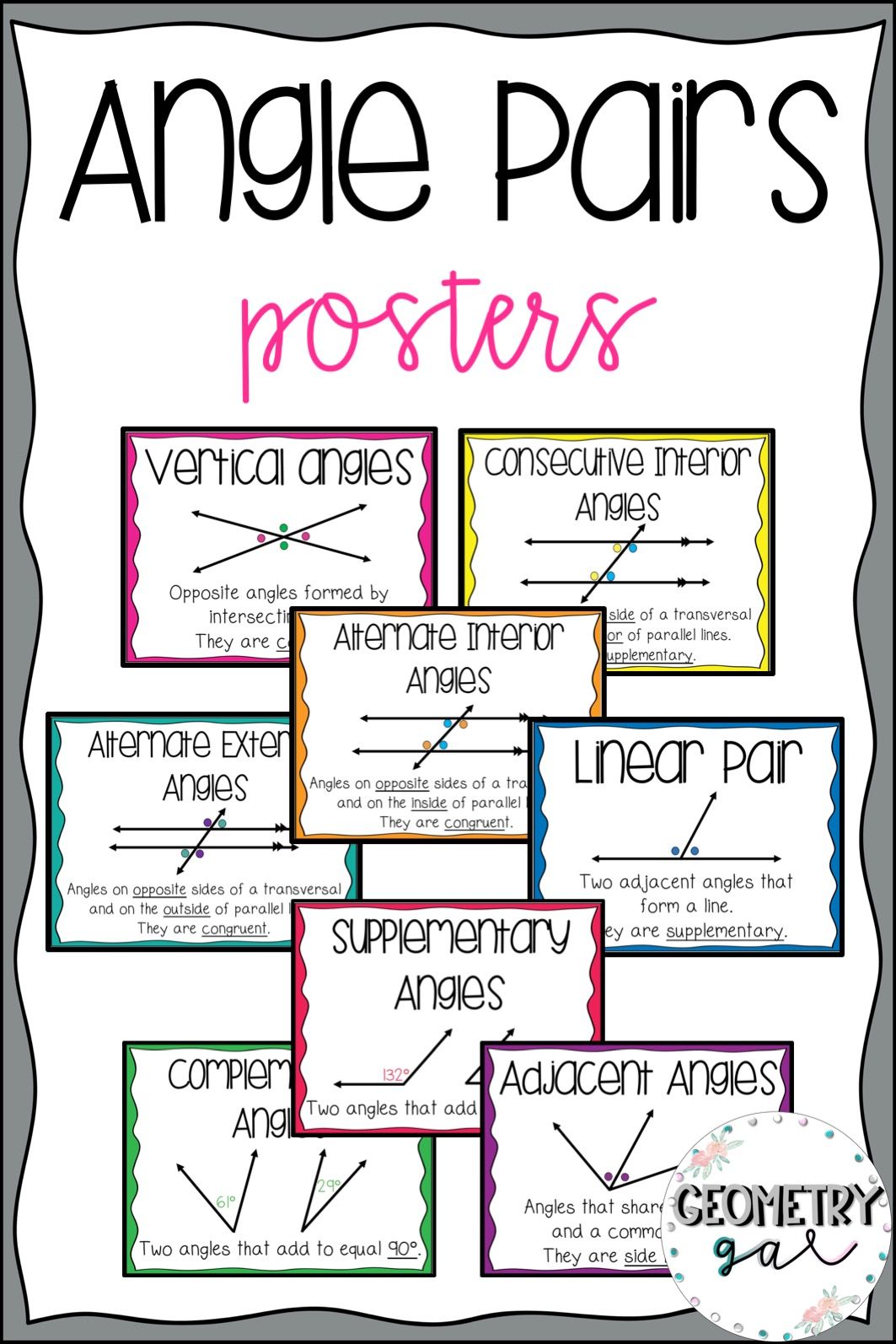
Vertical Angles


Vertical angles are perhaps the simplest to understand. Formed by two intersecting lines, these angles are opposite to each other and share the same vertex.
- Definition: When two lines intersect, four angles are formed. The pairs of angles that are opposite to each other are called vertical angles.
- Properties: Vertical angles are always equal in measure, which can be mathematically proven with the fact that linear pairs are supplementary (sum to 180°).
Here's a quick look at how you might identify vertical angles in your worksheet:
| Figure | Vertical Angle Pairs |
|---|---|
 |
∠1 = ∠3, ∠2 = ∠4 |
 |
∠A = ∠C, ∠B = ∠D |

📚 Note: Always verify your identification of vertical angles by checking if they are directly across from each other when two lines cross.
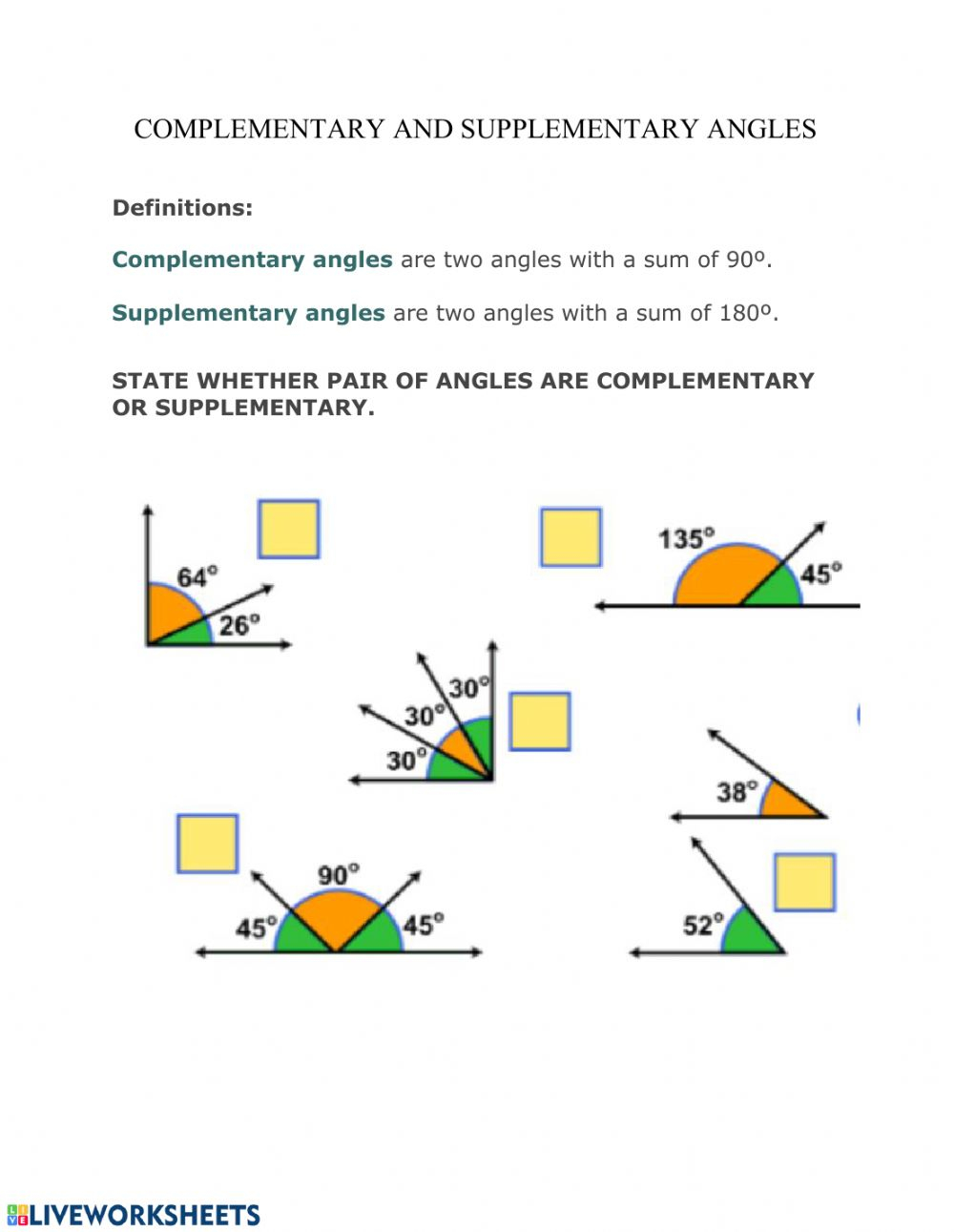
Supplementary Angles

When two angles share a common vertex and together form a straight line, they are known as supplementary angles.
- Definition: Two angles are supplementary if their sum equals 180°.
- Types: Linear pairs and angles on a straight line are the most common examples.
Here are some examples from the worksheet:
- ∠A and ∠B are supplementary if ∠A + ∠B = 180°.
- Given ∠C = 60°, then its supplementary angle would be 120° (180° - 60°).
Complementary Angles

These angles add up to 90°, creating a right angle.
- Definition: Two angles are complementary if their sum is 90°.
- Example: An angle of 30° and an angle of 60° are complementary because 30° + 60° = 90°.
Consider these scenarios from the worksheet:
- ∠D and ∠E are complementary if ∠D + ∠E = 90°.
- If ∠F = 45°, then ∠G, its complement, must be 45° (90° - 45°).
Adjacent Angles
Adjacent angles are two angles that share a common vertex, a common arm, and no internal points.
- Definition: Angles that are next to each other and share a side.
- Example: If you draw two intersecting lines, the angles at the intersection that do not overlap are adjacent.
From the worksheet:
- ∠H and ∠I are adjacent if they share the same arm.
- These angles might or might not be supplementary depending on their positions.
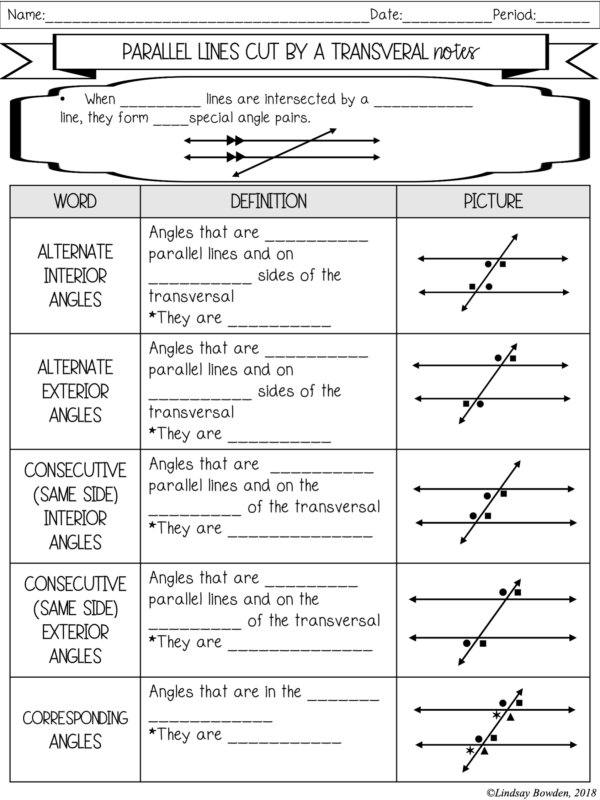
Alternate Interior and Exterior Angles
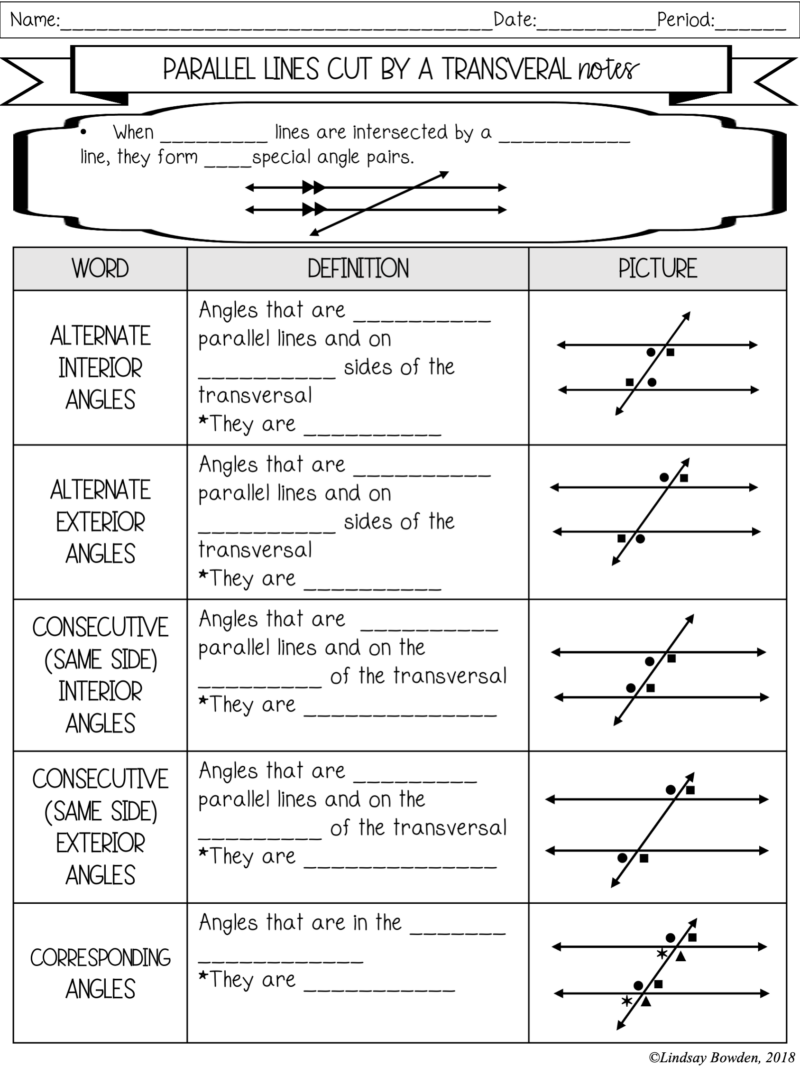
When a transversal crosses two parallel lines, several types of special angle pairs are formed:
- Alternate Interior Angles: These are non-adjacent angles on opposite sides of the transversal between the two parallel lines.
- Alternate Exterior Angles: Similar to interior, but on the outside of the parallel lines.
Here's how they might appear in your worksheet:
- ∠J and ∠K are alternate interior angles, as are ∠L and ∠M.
- These angles are congruent, meaning ∠J = ∠K and ∠L = ∠M.
Corresponding Angles

Corresponding angles are located in the same relative position at each intersection where the transversal cuts through the parallel lines.
- Definition: They occupy corresponding positions when lines are crossed by a transversal.
- Example: ∠N = ∠O if line 'l' is parallel to line 'm'.
These relationships can be crucial for solving geometry problems involving parallel lines and transversals:
- If you know ∠P, you can find corresponding ∠Q since they are equal in measure.
Co-Interior Angles
Also known as consecutive interior angles, these pairs are on the same side of the transversal and inside the parallel lines.
- Definition: Angles formed between the transversal and two parallel lines on the same side.
- Properties: They are supplementary, meaning their sum equals 180°.
To find co-interior angles in your worksheet:
- Identify ∠R and ∠S as co-interior if they are between parallel lines and on the same side of the transversal.
Applying Angle Pair Properties in Real World
Understanding special angle pairs goes beyond academic exercises; it has practical applications:
- Architecture: Determining angles for roof pitches and staircases.
- Surveying: Using angles to calculate distances and map locations.
- Navigation: Pilots and sailors use angles to chart courses and find bearings.
These examples show how the knowledge of special angle pairs can be integral to various professions, demonstrating their real-world relevance.
What are vertical angles?

+
Vertical angles are pairs of opposite angles formed by two intersecting lines. They are equal in measure.
How can I identify alternate interior angles?

+
Look for angles inside the parallel lines on opposite sides of the transversal. If one angle is given, the alternate interior angle will be equal in measure.
What is the difference between supplementary and complementary angles?
+
Supplementary angles add up to 180°, while complementary angles add up to 90°.
Why are co-interior angles important?

+
Co-interior angles help in understanding the properties of parallel lines and transversals, which are essential in geometry for solving various angle problems.