7 Essential Tips for Mastering Special Angle Pairs

Learning about angles and their unique pairs can be a pivotal part of understanding both geometry and trigonometry. Whether you're studying these for school, enhancing your skills in design, or working in engineering fields, grasping the intricacies of angle pairs will offer invaluable insight into spatial relationships and mathematical problem-solving. Here are 7 essential tips that will help you master special angle pairs:
Understanding Adjacent, Vertical, Supplementary, and Complementary Angles

Angles can be categorized into various types based on their positional relationship. Here's a brief overview:
- Adjacent Angles: Share a vertex and a common side.
- Vertical Angles: Formed by intersecting lines; they are equal in measure.
- Supplementary Angles: Angles whose measures add up to 180 degrees.
- Complementary Angles: Angles whose measures add up to 90 degrees.
Remembering these relationships is fundamental because they often appear in proofs and problems involving symmetry, alignment, and geometry calculations.
Recognizing Linear Pair Angles
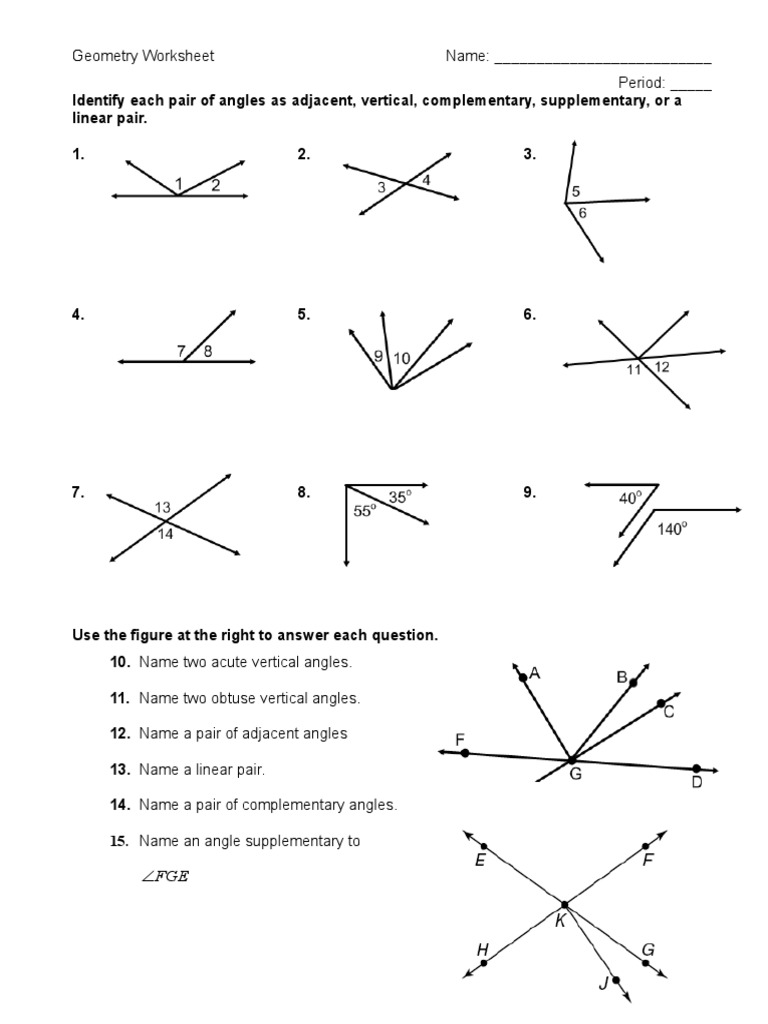
Linear pair angles are adjacent and supplementary. Here's a simple trick to recognize them:
- If two angles form a straight line, they are linear pairs.
⚠️ Note: When you see angles forming a straight line, they will add up to 180°
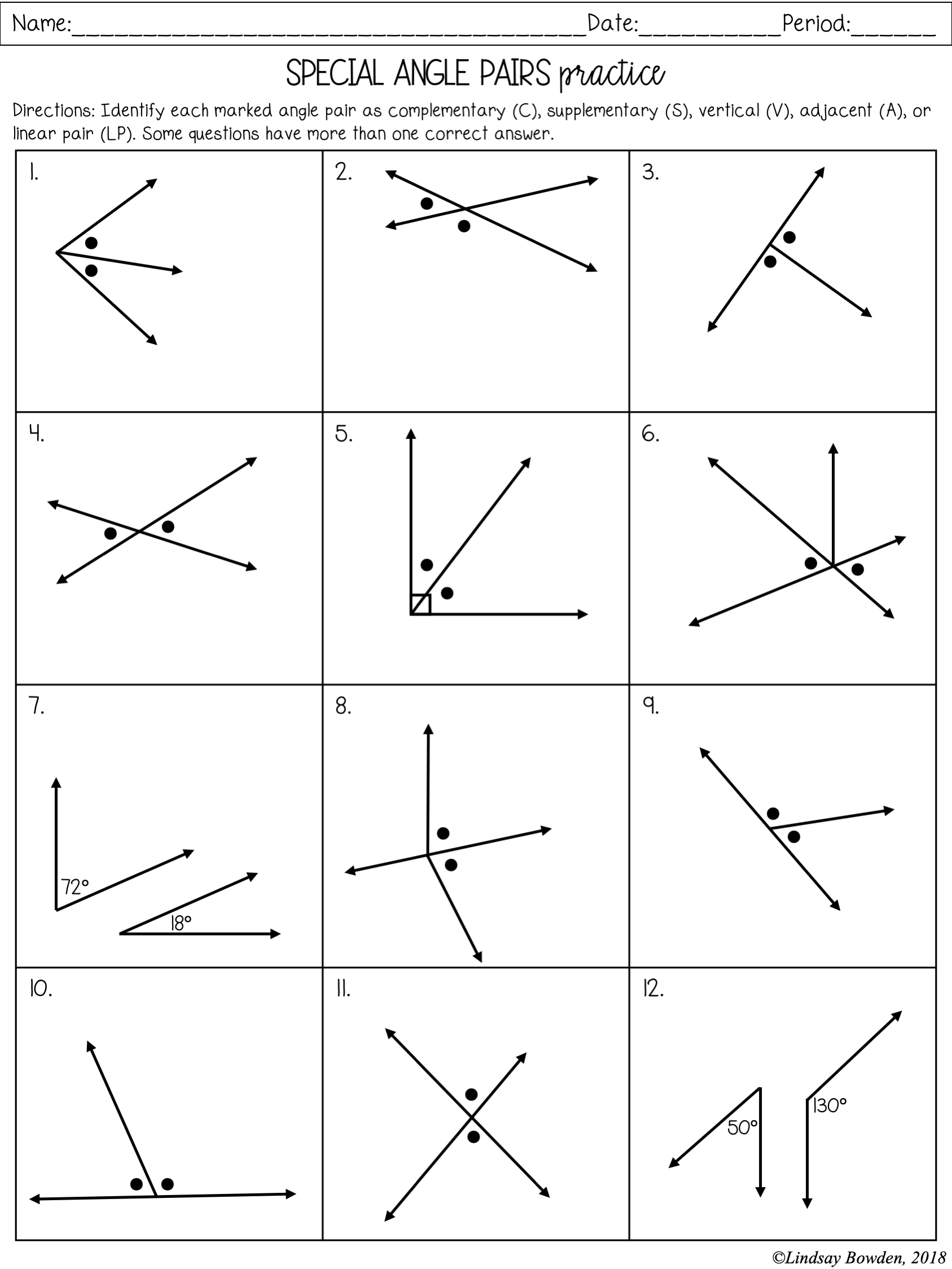
Practicing with Diagrams
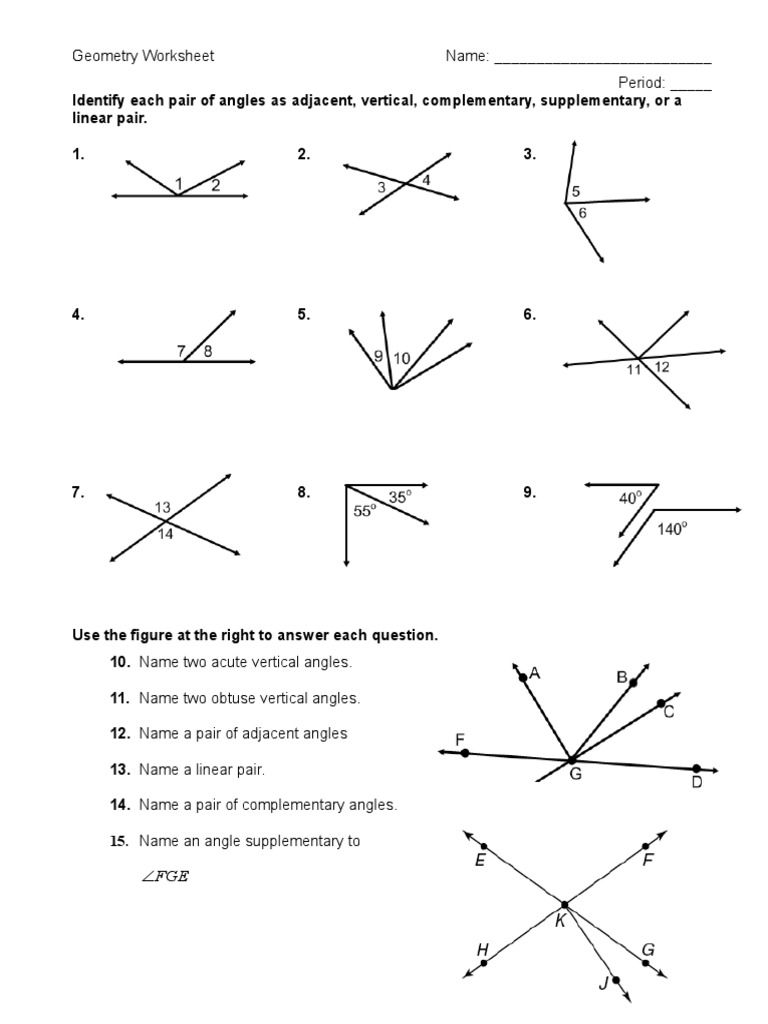
Visual aids are incredible for understanding angle pairs. Here's how you can utilize them:
- Sketch angles and label them to visualize their relationships.
- Use geometric software or graph paper to create precise diagrams.
- Solve problems by drawing what you're reading or discussing. This practice enhances spatial awareness.
Table of visual representation techniques:
| Type | Examples |
|---|---|
| Paper & Pencil | Quick sketches, graph paper diagrams |
| Software Tools | GeoGebra, Desmos, Autocad |
| Online Simulators | Khan Academy Geometry tool |

Using Algebra to Solve Angle Problems

Angles are not just visual; they can be algebraic puzzles too:
- Formulate equations based on angle relationships.
- Use known angles to solve for unknown angles.
- Remember the key equations like Complementary angles: A + B = 90° or Supplementary angles: A + B = 180°.
Incorporating Proofs in Your Studies

Proofs can be daunting, but they are essential for deep understanding:
- Start with simple proofs to solidify your understanding of definitions.
- Work through angle relationships using logical steps.
- Prove why angles are equal, supplementary, or complementary by employing geometric properties.
Exploring Real-World Applications

Angles aren't confined to textbooks; they have tangible applications:
- Architecture: Use angle pair calculations to ensure structures have proper alignments.
- Surveying: Use angles to determine land measurements and boundaries.
- Design: Apply angles in graphics, layout design, and product packaging to achieve aesthetics or functional outcomes.
💡 Note: Seeing how angles function in real life scenarios can deepen your understanding and make learning more relevant.
Staying Curious and Persistent

Mathematics, especially geometry, requires a curious mind:
- Explore how changing one angle affects others in a diagram.
- Look for patterns in your solutions, which can lead to shortcuts or deeper insights.
- Don't shy away from complex problems; tackle them with patience and persistence.
The journey to mastering angle pairs is continuous. Keep questioning, exploring, and applying these concepts in various contexts.
These tips serve as a roadmap to better comprehend special angle pairs. Whether you're aiming to excel in your academics or you're a professional looking to apply these principles in the real world, these strategies will help you navigate through the intricate world of angles. By practicing, understanding the theory, and seeing angles in practice, you're well on your way to mastering this essential geometric component.
What are some common types of special angle pairs?

+
Common types include adjacent, vertical, supplementary, complementary, and linear pair angles.
Why is it important to practice with diagrams?

+
Diagrams provide a visual context that helps in understanding spatial relationships and enhancing problem-solving skills.
How can algebraic skills help in geometry?
+
Algebra allows for setting up and solving equations related to angle measurements, making complex geometric problems manageable.
Can angle pairs be applied outside of theoretical mathematics?

+
Absolutely! Angle pairs are crucial in fields like architecture, surveying, computer graphics, and more.
Related Terms:
- Special angle pairs worksheet pdf
- Angle pairs Worksheet PDF
- Angle pairs Worksheet grade 7
- Special angle pairs worksheet answers