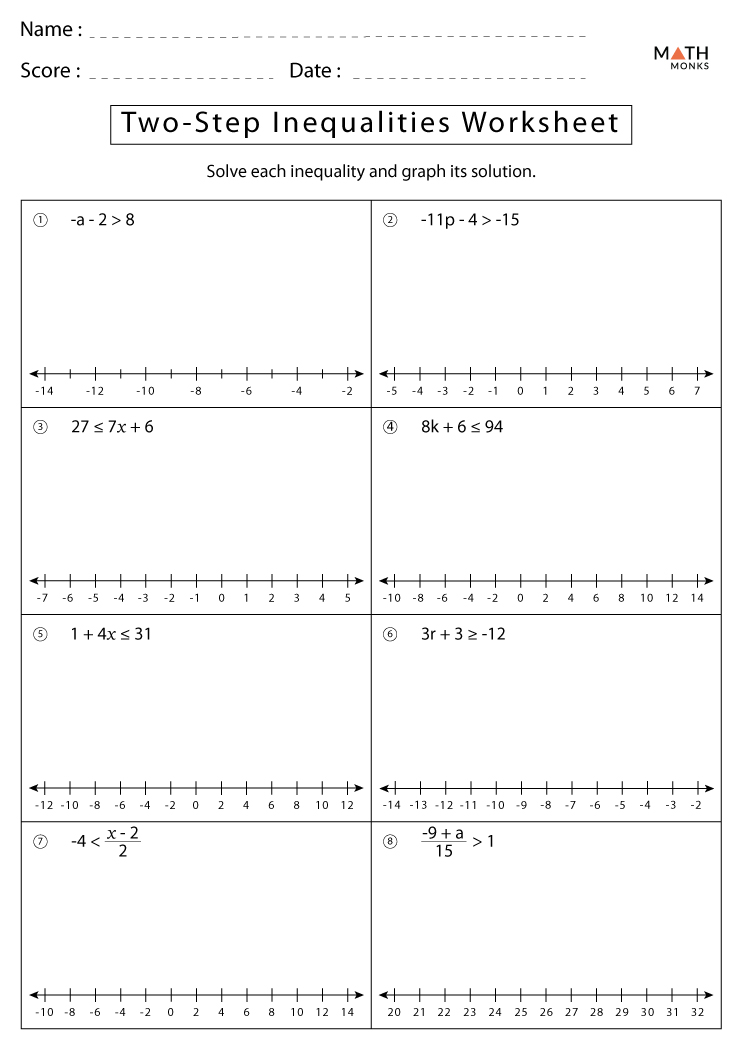
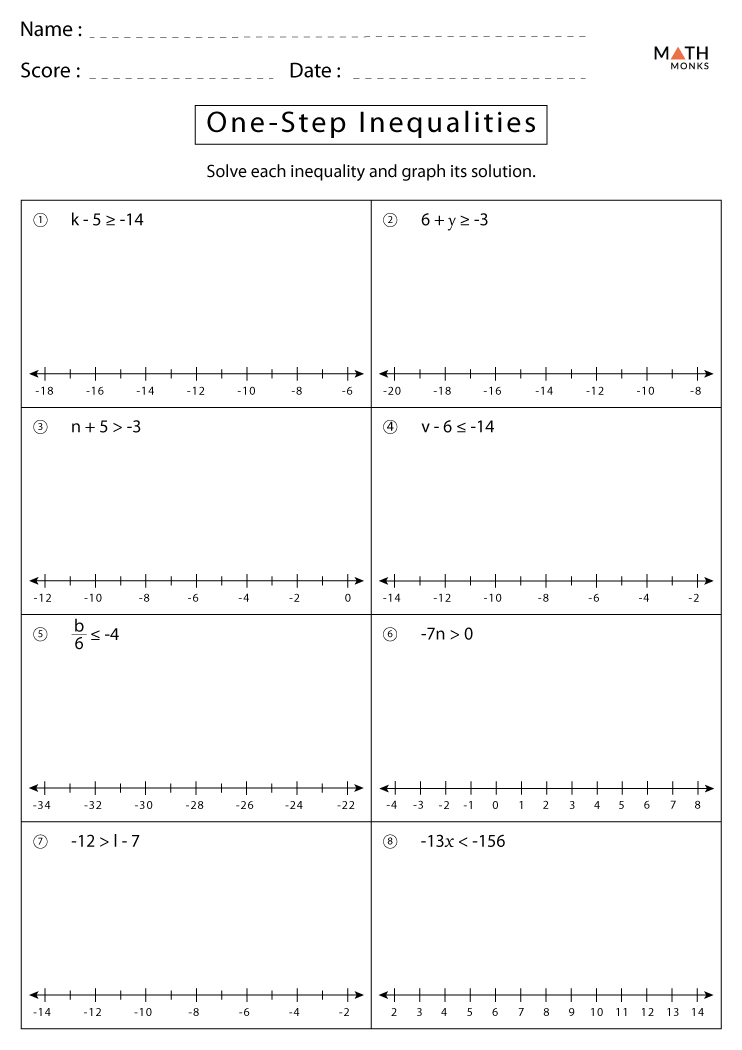
7 Steps to Master Two-Step Inequalities With Answers

Understanding two-step inequalities is an essential part of algebra that empowers students to solve real-world problems involving ranges rather than single points. By mastering the process of solving these inequalities, learners not only sharpen their critical thinking skills but also gain proficiency in a foundational aspect of mathematics that is applicable in diverse fields such as economics, engineering, and data analysis. In this comprehensive guide, we'll walk through the seven pivotal steps to solve two-step inequalities effectively.
Step 1: Understand the Structure


Before diving into solving inequalities, it’s crucial to grasp their basic structure. Unlike equations, inequalities have a solution set rather than a single solution, and they can be expressed with symbols like <, >, ≤, or ≥.
Formulating the Inequality

- Variable - The variable for which we solve.
- Constants - Fixed numbers involved.
- Signs - Inequality signs that guide us in finding the range of values.
💡 Note: Recognizing these elements will make your process of solving inequalities smoother.
Step 2: Isolate the Variable

To solve a two-step inequality, your first task is to isolate the variable term on one side of the inequality sign. This involves:
- Removing any constants that are added or subtracted from the variable term.
- Dividing or multiplying by any coefficient to get the variable alone.
Let's consider an example:
Example: 3x + 4 < 10
Here, we want to get x alone. We'll start by subtracting 4 from both sides:
3x + 4 - 4 < 10 - 4
This simplifies to:
3x < 6
Step 3: Flip the Inequality Sign
Remember that if you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality sign. Let’s continue our example:
From 3x < 6, to isolate x, we’ll divide both sides by 3:
3x / 3 < 6 / 3
This gives:
x < 2
📝 Note: Reversing the inequality sign when necessary is a critical step to ensure the validity of your solution.
Step 4: Simplify the Inequalities

After isolating the variable, simplify the inequality to its most readable form. If you have complex terms, simplify them if possible:
- Factor out common terms.
- Combine like terms on one side.
- Get rid of any fractions or decimals by multiplying through by the LCD (Lowest Common Denominator).
Step 5: Determine the Range of Solutions

After simplifying, you have the inequality in a form where the variable is isolated. Now, interpret this to find the range of solutions:
- For x < 2, the solution set includes all real numbers less than 2.
- For x ≤ -5, the solution set includes all real numbers less than or equal to -5.
Step 6: Graph the Solution

Graphing the solution is not only a visual aid but also a method to check if your solution makes sense. Here’s how to graph:
- Draw a number line.
- If the inequality includes an equal sign (≤, ≥), use a solid dot at the boundary.
- If it does not include an equal sign (<, >), use an open dot.
- Shade the appropriate region on the number line to indicate the solution set.
Step 7: Interpret and Apply

With the solution set graphed, you can now interpret the results in the context of real-world problems or check for correctness:
- Consider if your solution set is practical for the problem at hand.
- Check if your inequality matches the conditions given in the problem.
The mastery of two-step inequalities opens a door to solving more complex problems in mathematics and beyond. By breaking down each inequality into manageable steps, you ensure accuracy, enhance comprehension, and can apply this knowledge to numerous practical scenarios where not just knowing a single solution, but a range of solutions, is beneficial.
What is the difference between an equation and an inequality?

+
An equation has one specific solution, while an inequality has a set of solutions that can be represented on a number line. Inequalities deal with ranges of values rather than just one value.
Why do we reverse the inequality sign?
+
Multiplying or dividing both sides of an inequality by a negative number reverses the relationship between the two sides, so the inequality sign must also be reversed to maintain the truth of the inequality.
Can inequalities have complex numbers as solutions?
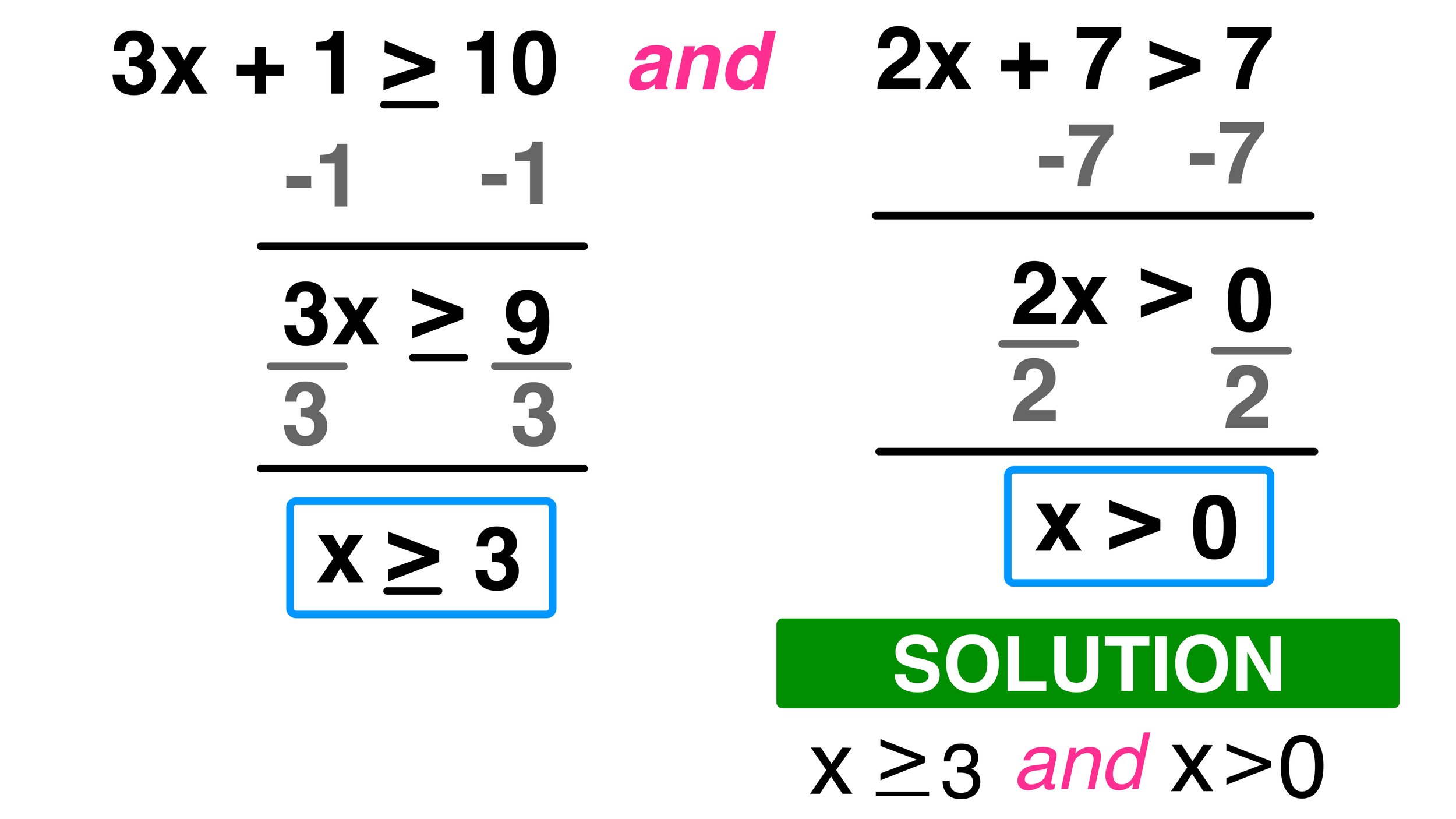
+
Yes, but in basic algebra, we usually deal with real number solutions. However, complex numbers can indeed be solutions to inequalities in advanced mathematics.
How do you solve an inequality with absolute value?

+
To solve an inequality involving absolute value, you set up two inequalities: one for the positive part and one for the negative part, then solve each part separately.
Can we always graph an inequality?

+
Yes, inequalities can always be graphed, either on a number line for one variable or on a coordinate plane for two or more variables, providing a visual representation of the solution set.