5 Easy Steps to Solve Two-Step Equations

Delving into the world of algebra can be both fascinating and intimidating. Mastering two-step equations is a pivotal step in this journey, serving as a bridge from simple algebraic expressions to more complex calculations. Here, we will explore 5 easy steps to solve two-step equations, ensuring that these foundational algebraic problems become second nature for students and mathematics enthusiasts alike.
The Basics of Two-Step Equations

Before jumping into the steps, understanding the essence of a two-step equation is crucial. These equations involve two operations, typically addition or subtraction followed by multiplication or division. Here's a simple example:
2x + 5 = 11
This equation requires us to isolate the variable 'x' by undoing the operations performed on it, step by step.
Step 1: Remove the Addition/Subtraction

The first step in solving a two-step equation is to get rid of the constant (the term not involving the variable) on the same side as the variable. This can be done by:
- Subtracting the constant if it's added.
- Adding the constant if it's subtracted.
Example:
2x + 5 = 11 Subtract 5 from both sides: 2x + 5 - 5 = 11 - 5 2x = 6

Step 2: Remove the Multiplication/Division

With the addition or subtraction part resolved, we now focus on isolating 'x' by undoing the multiplication or division:
- Dividing both sides if the variable is multiplied.
- Multiplying both sides if the variable is divided.
Example:
2x = 6 Divide both sides by 2: (2x) / 2 = 6 / 2 x = 3

Step 3: Check Your Answer

After solving, it's always a good practice to verify if our solution is correct. Substitute the found value back into the original equation:
2(3) + 5 = 11 6 + 5 = 11 11 = 11
If both sides of the equation hold true, then the solution is correct. This step fosters confidence in the problem-solving process.
Step 4: Practice with Negative Numbers

Not all two-step equations are straightforward; some involve negative numbers, which can initially seem trickier. However, the steps remain the same:
- Remove the negative constant by performing the opposite operation.
- Isolate the variable by dividing or multiplying as necessary.
Example:
-2x + 3 = -1 Subtract 3: -2x + 3 - 3 = -1 - 3 -2x = -4 Divide by -2: x = 2
Check:
-2(2) + 3 = -1 -4 + 3 = -1 -1 = -1
Step 5: Handle Variables on Both Sides

When variables appear on both sides of the equation, it introduces an extra step to simplify the process:
- Move all variables to one side using addition or subtraction.
- Then proceed with the standard two-step equation-solving steps.
Example:
5x + 4 = 2x + 10 Subtract 2x from both sides: 5x - 2x + 4 = 2x - 2x + 10 3x + 4 = 10 Subtract 4: 3x + 4 - 4 = 10 - 4 3x = 6 Divide by 3: x = 2
Check:
5(2) + 4 = 2(2) + 10 10 + 4 = 4 + 10 14 = 14
💡 Note: Always remember, these steps are procedural and can be applied to almost all two-step equations, making algebra more manageable with practice.
Understanding how to solve two-step equations is not just about rote learning but about developing logical reasoning and pattern recognition. These skills are invaluable in higher math and real-life problem solving. Once you've gone through these steps several times, they'll start to become intuitive, allowing you to quickly solve equations by understanding the underlying principles.
What if my equation has parentheses?

+
First, distribute the number outside the parentheses to everything inside. Then proceed with the standard two-step equation solving process.
Why do we need to check our answers?

+
Checking answers ensures the solution is accurate and builds confidence in your problem-solving abilities. It’s easy to make small errors, and verifying helps catch these.
Can these steps be applied to equations with more than two variables?
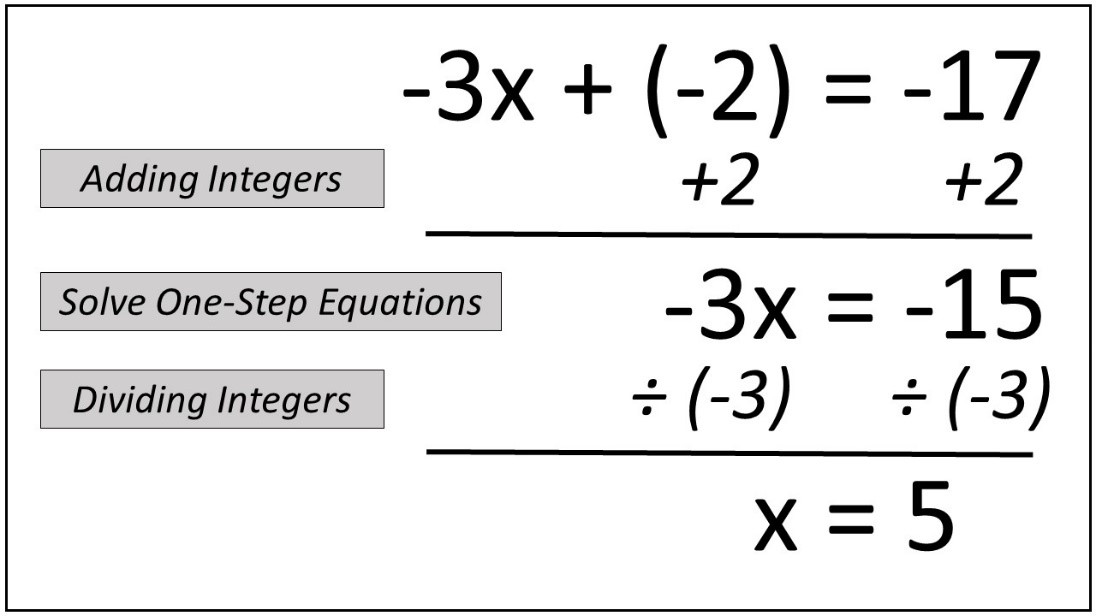
+
No, these steps are specifically designed for two-step equations with one variable. For equations with multiple variables or steps, more complex methods like substitution or elimination are required.
Is it necessary to always isolate the variable on the left side?

+
No, you can choose either side to isolate the variable, but consistency can make the process easier and less error-prone.
What if I have a negative variable?

+
Treat the variable as a positive value, but remember to apply the correct sign when solving. The steps are the same; you’ll just need to keep track of the sign changes.