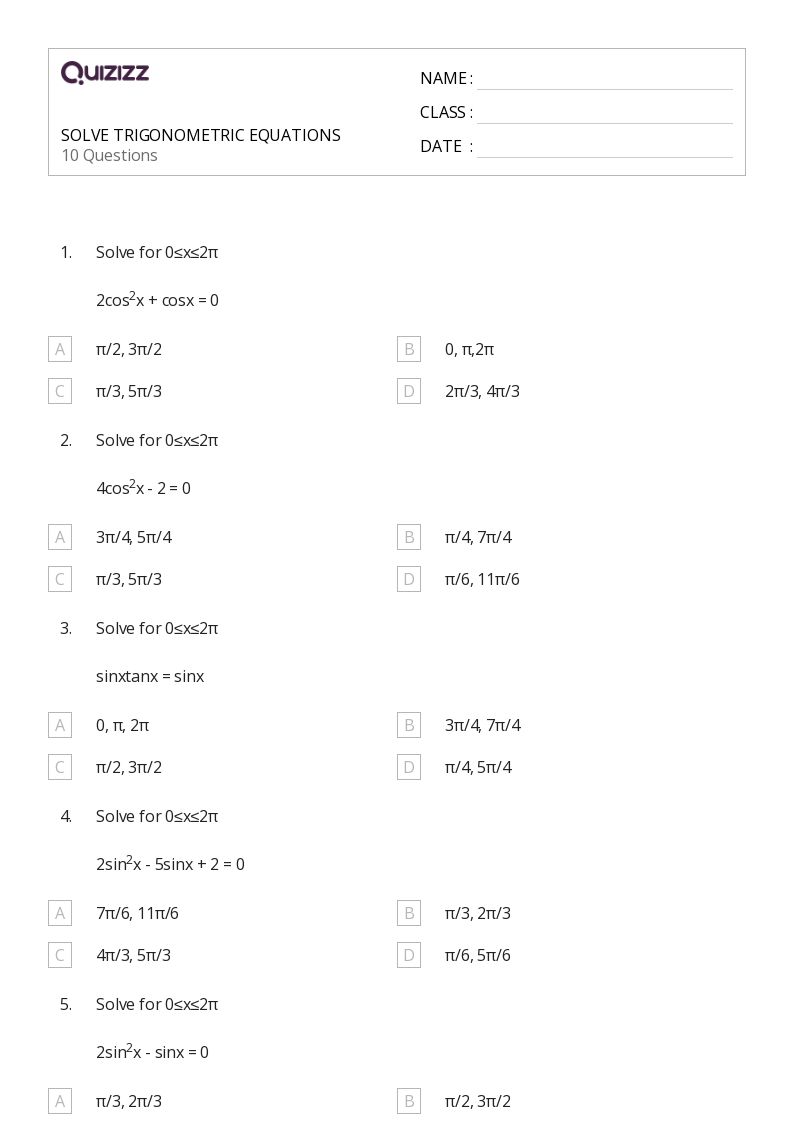
Master Trigonometric Equations with This Fun Worksheet

Trigonometry, often seen as one of the more challenging branches of mathematics, can be incredibly fun once you get the hang of it. At the heart of trigonometry are the equations, which can initially seem like a complex puzzle. However, with the right tools and a bit of practice, solving trigonometric equations can become a rewarding puzzle-solving adventure. In this blog post, we'll delve into trigonometric equations through an engaging worksheet designed to make learning both fun and effective.
Why Trigonometric Equations?

Before we dive into the worksheet, let’s explore why understanding trigonometric equations is vital:
- Practical Applications: Trigonometric equations find their use in various fields like engineering, physics, astronomy, and even in video game development for realistic animations.
- Problem-Solving Skills: Engaging with trig equations enhances your logical reasoning and problem-solving abilities.
- Mathematical Proficiency: Mastery over these equations opens up higher mathematical concepts, preparing you for more advanced studies.
Worksheet Overview
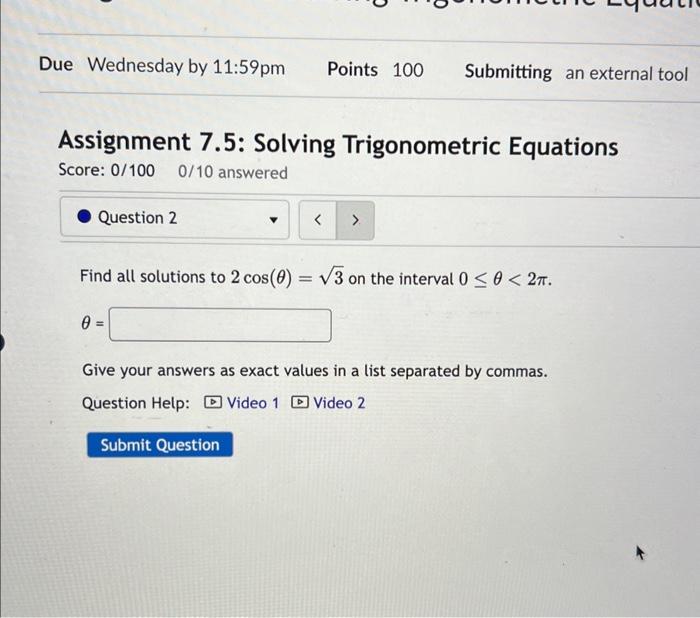
This worksheet is crafted to guide you through trigonometric equations with a step-by-step approach. Here’s what you’ll find:
- Basic to Advanced Equations: Starting with simple linear trigonometric equations and progressing to more complex quadratic and exponential forms.
- Visual Aids: Diagrams to illustrate geometric relationships in equations.
- Real-world Problems: Examples that relate to real-life scenarios to keep the learning practical.
Worksheet Contents
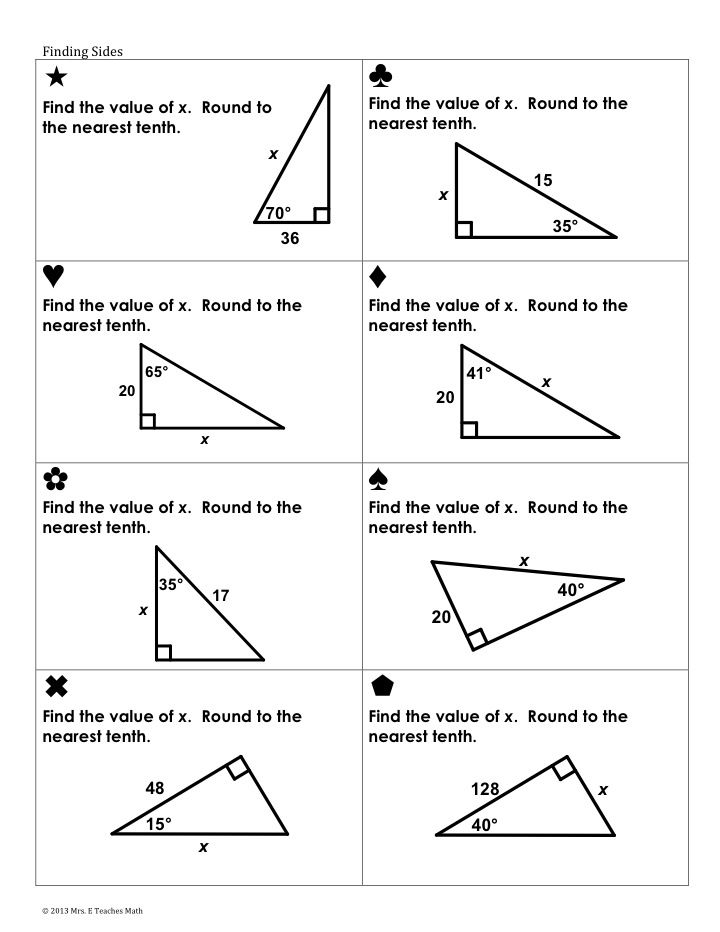
Part 1: Linear Trigonometric Equations

In this section, we’ll solve equations like:
- sin(x) = 0.5
- 2cos(x) + 1 = 0
⚠️ Note: Remember, sin(x) = 0.5 has multiple solutions within [0, 2π].
Part 2: Quadratic Trigonometric Equations

Here, we’ll tackle:
- tan²(x) - tan(x) - 1 = 0
- sin²(x) - cos(x) = 0
| Equation | Solutions | Method |
|---|---|---|
| sin²(x) - cos(x) = 0 | x = π/4, 5π/4 | Convert to sin(x)(sin(x) - 1) = 0 |

Part 3: Exponential Trigonometric Equations

We’ll explore equations like:
- tan(2x) = tan(x)
- 2sin(x) = cos(2x)
Strategies for Solving Trigonometric Equations

1. Identify the Basic Function
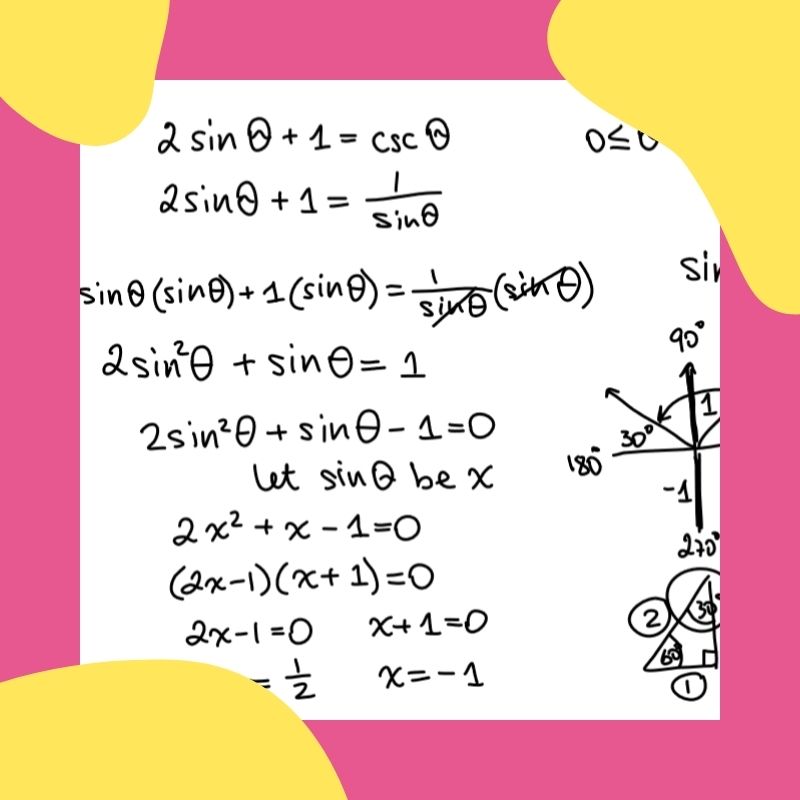
Before diving into complex algebra, it’s crucial to identify the basic trigonometric function you’re dealing with:
- Sine, Cosine, or Tangent?
- Is it a linear, quadratic, or higher-order equation?
2. Use Trigonometric Identities

Leverage identities like:
- sin(2x) = 2sin(x)cos(x)
- cos²(x) + sin²(x) = 1
- tan(x) = sin(x) / cos(x)
🔍 Note: Applying identities can simplify complex equations dramatically.
3. Find the Periodicity

Trigonometric functions repeat their values over a period. Understanding periodicity helps in:
- Finding all possible solutions within one period.
- Extending solutions beyond a single period.
4. Solve for General Solution

Once you have the solutions within one period:
- Generalize the solutions using the periodicity of the function.
- Convert to an equation form like x = πk or x = π/4 + πk where k is an integer.
5. Practice with Real-World Scenarios
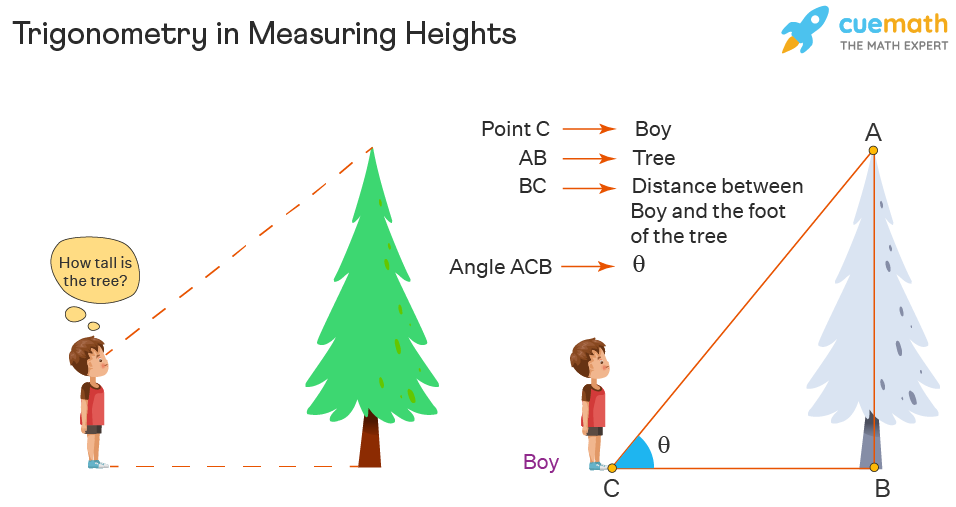
Applying trigonometric equations to real-world problems:
- Analyze the problem for relevant trigonometric relationships.
- Set up the equation and solve it, verifying your results within the context of the problem.
Conclusion

Trigonometric equations, with their periodic and cyclic nature, offer a unique challenge that, when met, enhances your problem-solving capabilities and deepens your understanding of the interconnectedness of mathematics. Through the structured approach in this worksheet, we’ve moved from basic to more complex equations, illustrating key strategies that are universally applicable. Not only does this sharpen your technical skills, but it also encourages creative thinking by connecting abstract math to real-life situations. Mastering these equations paves the way for further exploration in both mathematics and the fields where trigonometry plays a pivotal role, from architecture to astrophysics. Remember, the journey through trigonometry is as enriching as the solutions you find, making every equation a puzzle piece in the grand mathematical picture.
What is the general solution to tan(x) = tan(y)?
+
The general solution is x = y + nπ, where n is any integer.
How do you solve a trigonometric equation involving more than one angle?

+
Use trigonometric identities to simplify the equation and then solve for the individual angles within the equation’s constraints.
Can trigonometric equations always be solved analytically?
+While most basic and quadratic trigonometric equations can be solved analytically, some complex ones might require numerical methods or computer algebra systems.
What are some practical applications of solving trigonometric equations?
+Trigonometric equations are used in surveying, navigation, solving problems in physics, and even in digital signal processing and cryptography.
Related Terms:
- Solving trigonometric equations worksheet pdf
- 7 5 solving Trigonometric Equations answers
- Solving Trig Equations Worksheet Kuta



