Mastering Triangle Solutions: Your Ultimate Worksheet Guide

Understanding geometry, particularly the study of triangles, is essential in various fields, from architecture and engineering to computer graphics and beyond. This comprehensive guide serves as your ultimate worksheet to mastering triangle solutions, providing you with the knowledge, skills, and tools you need to solve a multitude of triangle-related problems efficiently and effectively.
Basic Triangle Properties and Terminology

Before diving into complex calculations, it's critical to understand the foundational elements of triangles. Here are some key concepts:
- Vertices: The points where the sides of the triangle meet.
- Sides: The line segments connecting the vertices.
- Angles: The corners formed where two sides intersect.
- Classification by Sides: Triangles can be equilateral (all sides equal), isosceles (two sides equal), or scalene (all sides different).
- Classification by Angles: They are either acute (all angles less than 90°), right (one angle is exactly 90°), or obtuse (one angle more than 90°).
- Sum of Angles: The sum of internal angles in a triangle always equals 180°.
🔍 Note: Always identify the type of triangle before proceeding with calculations to simplify your problem-solving approach.
Calculating Area and Perimeter

Here's how you can determine the area and perimeter of various types of triangles:
Area of a Triangle

- Base and Height: Area = ½ * base * height.
- Heron's Formula: For any triangle when you know the length of all sides (a, b, c), use: Area = √[s(s - a)(s - b)(s - c)], where s is the semi-perimeter, s = (a + b + c) / 2.
- Right Triangle: For right triangles, if you know the legs (a and b), then Area = ½ * a * b.
Perimeter of a Triangle

- Simply sum the lengths of all sides: Perimeter = a + b + c.
🔍 Note: Heron's formula is especially useful when you don't know the height of the triangle.
Understanding Triangle Relationships

Recognizing and utilizing relationships between angles and sides can streamline your work in geometry:
- The Pythagorean Theorem: In a right triangle, a2 + b2 = c2, where c is the hypotenuse.
- Cosine Rule: For any triangle, c2 = a2 + b2 - 2ab cos(γ), where γ is the angle opposite side c.
- Sine Rule: In any triangle, sin(A) / a = sin(B) / b = sin(C) / c.
Solving Triangle Problems

To effectively solve triangle problems, consider the following steps:
Step-by-Step Process

- Identify: Determine if the triangle is equilateral, isosceles, scalene, acute, right, or obtuse.
- Gather Information: Collect known data like side lengths, angles, or any special conditions (e.g., right angle).
- Choose the Right Formula: Select the most appropriate method or formula based on the information available.
- Calculate: Perform necessary calculations step by step.
- Verify: Check your solution to ensure it fits within the bounds of triangle properties.
Worksheet Examples

Let's illustrate with a couple of examples:
| Problem | Solution Method |
|---|---|
| A triangle has sides 6, 8, and 10. Find the area. | Using Heron's formula since we know all sides. |
| A right triangle with legs of 3 and 4. Find the hypotenuse and area. | Use the Pythagorean Theorem for the hypotenuse and the area formula for right triangles. |
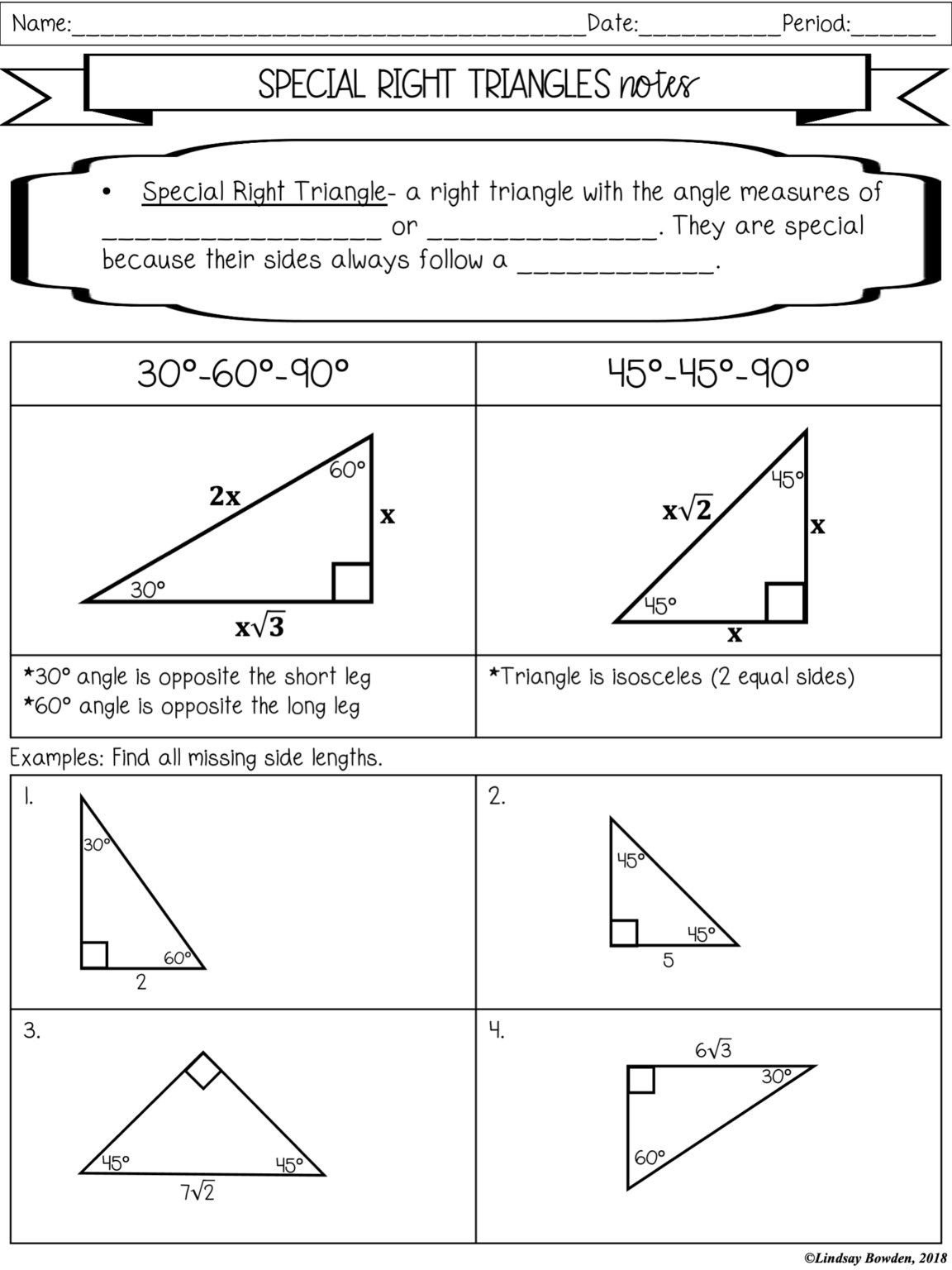
🔍 Note: When dealing with mixed units or different scales, ensure all measurements are in the same unit before calculations.
Advanced Techniques for Triangle Analysis

Once you grasp the basics, you can delve into more sophisticated methods:
- Coordinate Geometry: Using the coordinates of vertices to find distances, midpoints, and slopes, which can be instrumental in verifying properties like right angles or collinearity.
- Trigonometric Identities: Employ trigonometric functions for solving complex triangular arrangements or angles of elevation and depression in real-world applications.
By mastering these advanced techniques, you can handle more intricate geometric challenges and integrate this knowledge into fields such as navigation, surveying, and computer graphics.
Summarizing our journey through triangle solutions, we've covered fundamental properties, area and perimeter calculations, key relationships like the Pythagorean Theorem and trigonometric laws, and a systematic approach to solving problems. Understanding these elements not only enables you to tackle triangle-related challenges but also equips you with a versatile set of tools for various mathematical contexts.
How do I know if a triangle is right-angled using just its side lengths?

+
You can use the Pythagorean Theorem: If the square of the longest side (the hypotenuse) equals the sum of the squares of the other two sides, then it’s a right triangle.
Can I find the height of an obtuse triangle?

+
Yes, you can find the height of an obtuse triangle using trigonometry or by breaking it down into smaller triangles, or using the formula: Area = ½ * base * height, where height can be calculated using Heron’s formula.
What if I only know two angles in a triangle?

+
If you know two angles, you can find the third since the sum of angles in a triangle is 180°. With this knowledge, you can then use the Law of Sines or Cosines to solve for side lengths if needed.
How can I apply triangle solutions in real-world problems?

+
Triangle solutions are used in surveying to calculate distances, in architecture for stability and design, and in navigation for triangulation. They’re also crucial in computer graphics for rendering and in trigonometry for various real-life calculations.
Is there an easy way to remember these formulas?

+
Yes, mnemonic devices like SOHCAHTOA for sine, cosine, and tangent can help remember trigonometric relationships. For the Pythagorean Theorem, many remember it through various phrases or visual aids.



