Solving Systems of Equations Worksheet Mastery Guide

Understanding the Basics of Systems of Equations

Before diving into solving systems of equations, it’s essential to grasp what they represent. A system of equations is a set of two or more equations that share common variables. The goal is to find the values of these variables that make all equations in the system true at the same time. Here’s what you need to know:
- Linear vs. Non-Linear: Systems can be linear, where equations represent straight lines, or non-linear, which can include curves and parabolas.
- Types of Solutions:
- Unique Solution: When lines intersect at a single point.
- Infinite Solutions: When lines overlap, making every point a solution.
- No Solution: When lines are parallel.
Methods to Solve Systems of Equations

Let’s delve into the primary methods used to solve these systems:
Graphing

This visual method involves plotting each equation on a graph:
- Draw each line on the same coordinate plane.
- Identify the point of intersection, if any.
🔄 Note: This method is quick for visualizing, but less precise for finding exact solutions.
Substitution Method

Ideal for systems where one of the equations is easily solved for one variable:
- Isolate a variable in one equation.
- Substitute that expression into the other equation.
- Solve for the remaining variable, then substitute back to find all values.
Elimination Method
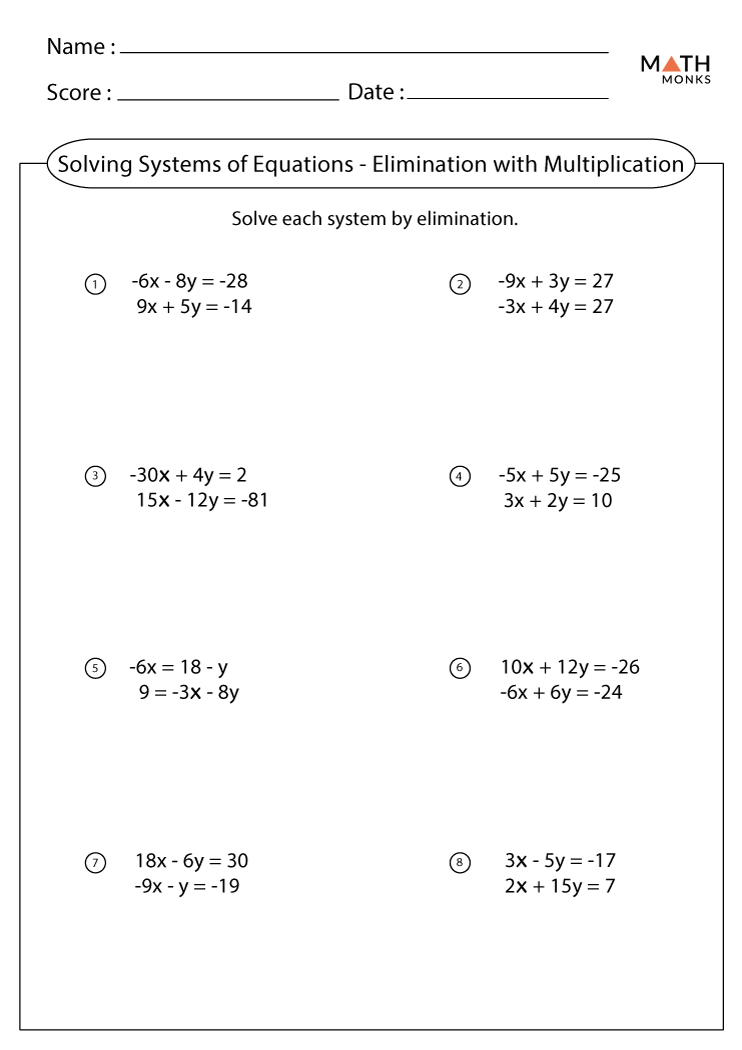
Use this when it’s straightforward to eliminate one variable by adding or subtracting the equations:
- Adjust equations so that coefficients of one variable are opposites.
- Add or subtract equations to eliminate a variable.
- Solve the resulting equation, then substitute back to find the other variable.
Matrix Method

A more advanced approach often used with the help of technology:
- Express the system as matrices (A, X, B).
- Solve AX = B by finding X through matrix inversion or Gaussian elimination.
Here’s a table summarizing when each method is most useful:
| Method | Best for |
|---|---|
| Graphing | Quick visual checks, rough estimation |
| Substitution | Easy variable isolation |
| Elimination | Coefficients that align easily for elimination |
| Matrix | Larger systems or when using technology for precision |

Practice with Solving Systems of Equations

To master solving systems of equations, consistent practice is key. Here are some strategies:
- Repetition: Work through problems regularly to solidify understanding.
- Variety: Practice different types of systems (linear, quadratic) with varied solution sets.
- Step by Step: Follow the methods outlined above for each problem to reinforce the process.
- Verification: Check your answers either by substitution or graphically.
Wrapping Up

In this guide, we’ve explored the fundamental concepts, methods, and strategies for mastering systems of equations. From understanding what systems of equations are to practicing them with different approaches, you’re now equipped with the knowledge to tackle these problems confidently. Remember, the beauty of systems of equations lies in their ability to represent real-world problems, making them a powerful tool in mathematical analysis.
What’s the difference between linear and non-linear systems of equations?

+
Linear systems involve equations where each term is either a constant or the product of a constant and a single variable raised to the first power. Non-linear systems include terms where variables are raised to powers other than one or involve products of variables.
Why would I choose the elimination method over substitution?

+
Choose elimination when it’s easy to manipulate the equations to have coefficients that align for elimination. It can be faster if you don’t need to isolate variables in one equation first, unlike with substitution.
How do I know if a system has no solution?

+
When solving systems graphically, if the lines are parallel, there’s no solution because they never intersect. Algebraically, you’ll reach a contradiction when trying to solve the system.
Is there a method best suited for solving larger systems?

+
For larger systems with many variables, the matrix method (using techniques like Gaussian elimination or matrix inversion) is often the most efficient, especially when assisted by computational tools.
Can systems of equations help solve real-world problems?

+
Yes, systems of equations are used in various fields like economics, engineering, and logistics to model complex scenarios where multiple unknowns interact, providing solutions to optimize or balance different factors.