5 Easy Steps to Solve Equations by Graphing

Whether you're a student tackling algebra for the first time or a professional engineer analyzing complex systems, understanding how to solve equations through graphing is a valuable skill. Graphing provides a visual and intuitive method to find the solutions of equations, whether they are linear, quadratic, or higher-order polynomials. This approach not only reinforces your understanding of mathematics but also gives you a tool to solve problems in physics, economics, and numerous other fields. Here, we'll explore five easy steps to master the art of solving equations by graphing.
Step 1: Understand the Basics of Graphing

Before diving into graphing to solve equations, you need a basic understanding of coordinate systems:
- Coordinate Plane: This is a plane with an x-axis (horizontal) and a y-axis (vertical). Points on this plane are defined by their x and y coordinates (x, y).
- Function: A function relates each input (x) to exactly one output (y). When graphing functions, we plot the points (x, f(x)) where f(x) is the equation's right-hand side.
📌 Note: Familiarity with plotting functions manually or using software can enhance your ability to solve equations graphically.
Step 2: Set Up Your Graph
Equip yourself with graph paper or graphing software to plot your equations accurately:
- Choose appropriate scales for the axes to fit the range of values your equations might produce.
- Label the axes clearly to keep track of your variables and their scales.
- If you're using digital tools, familiarize yourself with how to enter and plot equations.
Step 3: Graph the Equation(s)

Now, let's focus on plotting the equations:
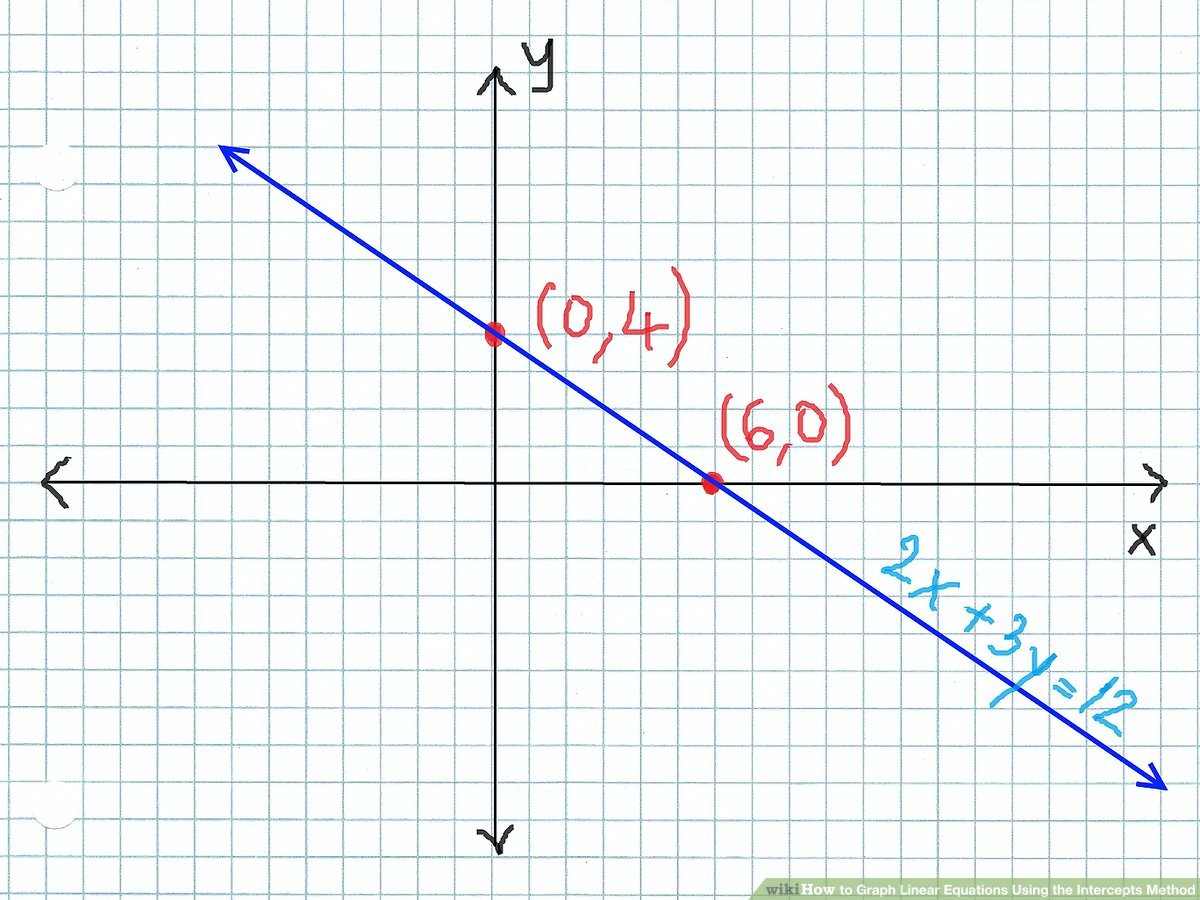
- Linear Equations: Linear equations like y = mx + b can be graphed by plotting two points and drawing a line through them. Another method involves the slope-intercept form to plot the y-intercept and use the slope to find the second point.
- Quadratic Equations: For quadratic equations (y = ax^2 + bx + c), plot points around the vertex and any intercepts. Or, use the vertex form or the quadratic formula to find key points.
- Higher-Order Polynomials: Use calculus for derivatives and find critical points or simply plot enough points to visualize the general shape of the curve.
When graphing, ensure you're using the correct order of operations and evaluating each term accurately.
| Equation Type | Characteristics | Graphing Tips |
|---|---|---|
| Linear | One solution unless parallel or identical | Use slope-intercept form |
| Quadratic | Can have 0, 1, or 2 solutions | Find vertex and intercepts |
| Higher-Order Polynomials | May have multiple solutions | Plot points and critical points |
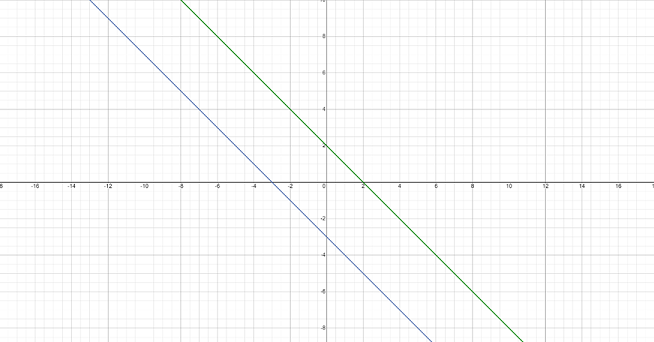
Step 4: Analyze the Graphs
Once you've plotted the equations, it's time to analyze them to find the solutions:
- Linear: The point of intersection of two lines is the solution to the system of equations. If lines are parallel, there's no solution. Identical lines have infinite solutions.
- Non-Linear: Look for where the lines or curves intersect each other. Each intersection represents a solution to the system of equations.
Don't forget to check for extraneous solutions by plugging them back into the original equations.
🌟 Note: In higher-order polynomials, don't be surprised if you find multiple or even imaginary solutions; these are still valid in the context of complex numbers.
Step 5: Verify Your Solutions

After identifying potential solutions graphically, it's important to verify them:
- Substitute the solutions back into the original equations to ensure they satisfy all conditions.
- Consider using algebraic methods like substitution or elimination as a cross-check for the graphical solutions.
🔎 Note: This step ensures accuracy, especially in complex systems where graphical errors can occur due to imprecise plotting or human error.
In this manner, solving equations by graphing can not only yield quick results but also provide insight into the behavior of functions. This method, once mastered, becomes an invaluable part of your mathematical toolkit, allowing you to analyze and predict outcomes visually before diving into the algebra.
From understanding the basics to verifying solutions, these five steps provide a structured approach to solving equations graphically. This approach offers a balance between visual intuition and mathematical precision, ensuring a comprehensive understanding of algebraic problems.
What’s the difference between algebraic and graphical solutions?

+
Algebraic solutions involve manipulating equations to isolate variables or eliminate unknowns. Graphical solutions rely on visually representing equations on a coordinate plane to find where they intersect, which indicates the solution points. While algebraic methods are precise, graphical methods provide a visual representation, which can be helpful for understanding the behavior of functions and spotting trends or patterns.
Can graphing solve all types of equations?

+
Graphing can effectively solve linear, quadratic, and polynomial equations of any degree, provided the solutions are real numbers. However, for equations with complex solutions or for systems with infinitely many solutions, graphing alone might not suffice. In such cases, algebraic or numerical methods are more appropriate.
How does one handle non-linear systems of equations?

+
Non-linear systems require a more intricate graphing approach. Plot the equations individually, looking for where they intersect. For more complex systems, you might need to use software to plot surfaces in 3D or manipulate the graphs to find intersections, sometimes even requiring implicit function plotting tools for systems like x^2 + y^2 = 25.