Systems by Elimination Worksheet: Quick Answer Guide
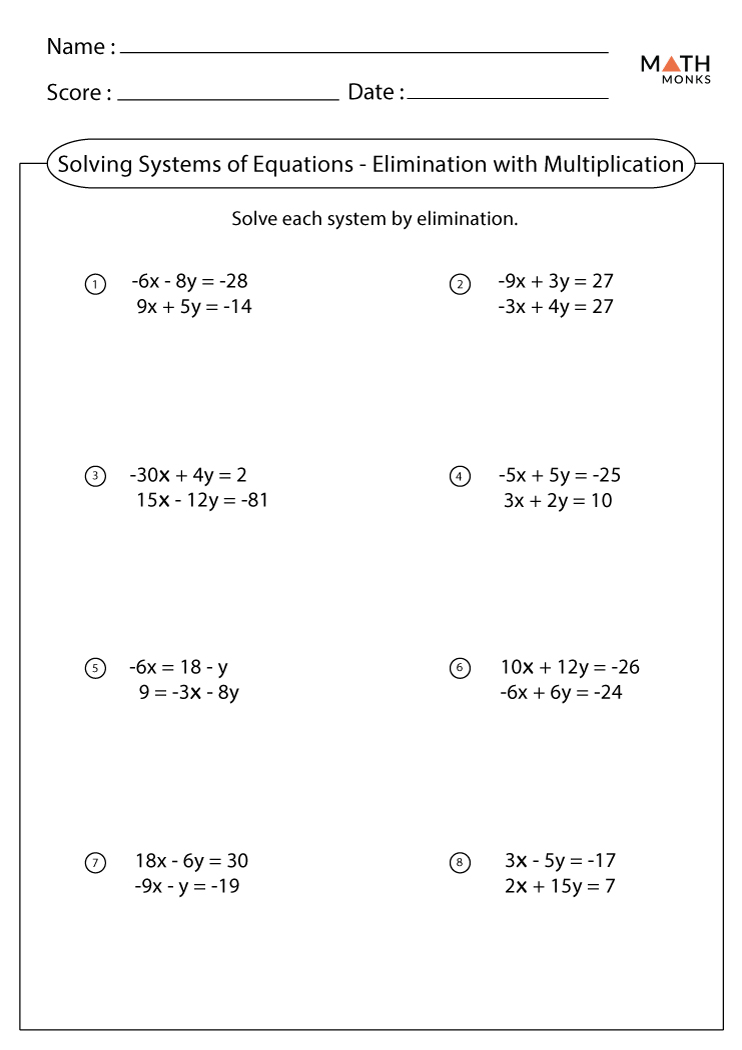
Systems of equations represent one of the fundamental algebraic concepts essential for both academic and real-world problem-solving. One of the most effective methods for solving systems of linear equations is the elimination method. This guide will walk you through the steps of using elimination to solve systems of equations, making it easier for students to understand and apply this method effectively.
Understanding the Elimination Method

Before diving into the steps, it's crucial to grasp what elimination entails:
- Elimination uses addition or subtraction to cancel out one of the variables in the system of equations.
- This results in an equation with one variable, which can then be solved to find its value.
- Substituting this value back into one of the original equations helps solve for the other variable.
Step-by-Step Guide to Solving Systems by Elimination

1. Setting Up Equations

Start with two equations:
- Equation 1: ax + by = c
- Equation 2: dx + ey = f
2. Choose Which Variable to Eliminate
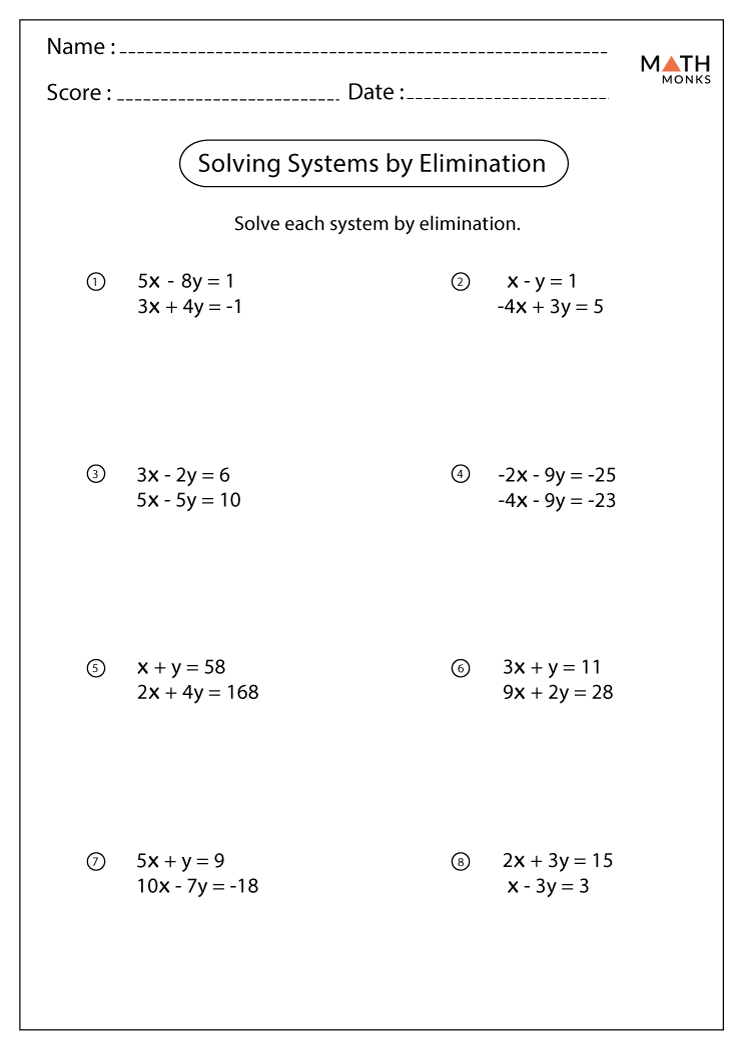
Decide which variable (x or y) you will eliminate:
- Look for coefficients that will make it easy to cancel out one of the variables. For instance, if both equations have the same coefficient for one variable, you can subtract or add the equations directly.
3. Multiply to Match Coefficients

If the coefficients don’t match:
- Multiply one or both equations by the necessary factor to ensure that the coefficients of the variable you want to eliminate are opposites or equal.
| Equation | Before Multiplication | After Multiplication |
|---|---|---|
| Equation 1 | 2x + 3y = 6 | 2x + 3y = 6 |
| Equation 2 | 3x + 2y = 4 | 2(3x + 2y = 4) → 6x + 4y = 8 |

🔍 Note: The aim here is to get the coefficients of one of the variables to be the same or additive inverses.
4. Add or Subtract the Equations

Combine the equations to eliminate one variable:
- Add the equations if the coefficients are opposites.
- Subtract the equations if the coefficients are the same.
5. Solve for the Remaining Variable

After eliminating one variable, you’ll have a simpler equation. Solve for the remaining variable:
(2x + 3y) - (6x + 4y) = 6 - 8
-4x - y = -2
y = 2 - 4x
6. Substitute Back to Find the Other Variable

Substitute the known value into one of the original equations to solve for the other variable:
- Using 2x + 3y = 6:
- 2x + 3(2 - 4x) = 6
- 2x + 6 - 12x = 6
- -10x + 6 = 6
- -10x = 0
- x = 0
7. Check Your Solution

Verify your solution by substituting the values back into the original equations:
- Substitute x = 0, y = 2 into both original equations to ensure they hold true.
🔎 Note: Checking your solution is crucial to ensure accuracy in your problem-solving process.
In this comprehensive guide, we’ve unraveled the intricacies of solving systems of equations through the elimination method. This technique not only simplifies complex problems but also empowers students to tackle various mathematical challenges with confidence. By following these steps, individuals can streamline their approach to solving systems of equations, enhancing their mathematical proficiency and problem-solving skills.
When should I use the elimination method over substitution?

+
The elimination method is particularly useful when one variable in both equations has coefficients that are easily cancellable or when substitution might lead to unnecessarily complex expressions.
What if none of the coefficients match for direct elimination?

+
If the coefficients don’t match, you can multiply one or both equations by constants to adjust the coefficients, ensuring they align for elimination.
Can the elimination method be used for more than two equations?

+
Yes, the elimination method can extend to solve systems with three or more equations, though the process might become more complex as you work to eliminate multiple variables simultaneously.
Related Terms:
- Solving systems by elimination calculator