Master Solving Equations with Our Graphing Worksheet Guide
Are you looking to master the art of solving equations in mathematics? Whether you're a student in high school or someone returning to math after a long hiatus, understanding how to solve equations can be both a fundamental skill and a challenging endeavor. This guide will take you through a comprehensive journey, using our Graphing Worksheet Guide, to not only solve equations but also to visualize them, aiding in a deeper understanding of algebra.
Why Graphing is Important in Solving Equations

Graphing equations can transform abstract numbers into visual representations, making the relationship between different variables more tangible. Here are several reasons why graphing is crucial:
- Visual Learning: For many, visual aids facilitate understanding, making complex equations more approachable.
- Identifying Patterns: Graphs help you see patterns in equations that might be less obvious when dealing with them algebraically.
- Real-World Application: Many real-life scenarios can be modeled and understood through graphing, from economic trends to scientific data.
📘 Note: Graphing provides not only a tool for solving but also for exploring mathematical concepts.
Getting Started with Our Graphing Worksheet
Our Graphing Worksheet is designed to ease you into the process of visualizing and solving equations. Here’s how you can begin:
- Familiarize Yourself with Coordinates: Understand the coordinate system, where the x-axis and y-axis intersect at the origin (0,0).
- Identify Key Elements: Learn to recognize different parts of a graph like the intercepts, slope, and any points where the function crosses the x or y-axis.
Let’s delve into a step-by-step process for using our worksheet:
1. Setting Up Your Graph

Begin by:
- Setting up the coordinate plane. Label your axes and decide on a suitable scale for your graph based on the equation’s range.
- Deciding on what intervals you’ll plot points (e.g., every 1 or 2 units).
2. Plotting the Equation

Here’s how to plot:
- Substitute values into the equation to find corresponding y-values. For linear equations (y = mx + b), choose x-values and calculate y. For more complex equations, use software or a graphing calculator to assist.
- Mark these points on your graph.
- Draw a smooth line or curve that passes through these points, considering the equation’s behavior.
3. Analyzing the Graph

Once plotted:
- Intercept Points: Find where the graph crosses the axes. This gives you solutions for x and y when one variable is zero.
- Maxima, Minima, and Zeros: Identify these for polynomial functions to understand the equation’s behavior.
Types of Equations and Their Graphs

Here’s a look at common equation types and how they appear when graphed:
| Type of Equation | Graph Characteristics |
|---|---|
| Linear (y = mx + b) | Straight line |
| Quadratic (y = ax² + bx + c) | Parabola |
| Cubic (y = ax³ + bx² + cx + d) | S-shaped curve |

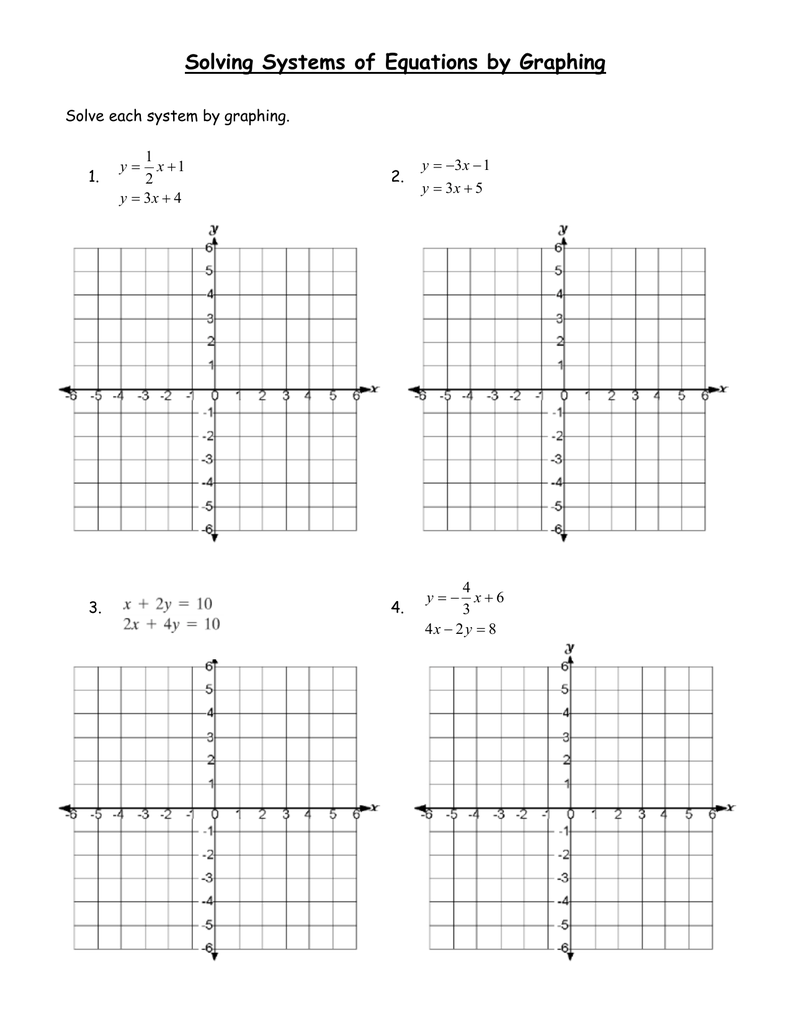
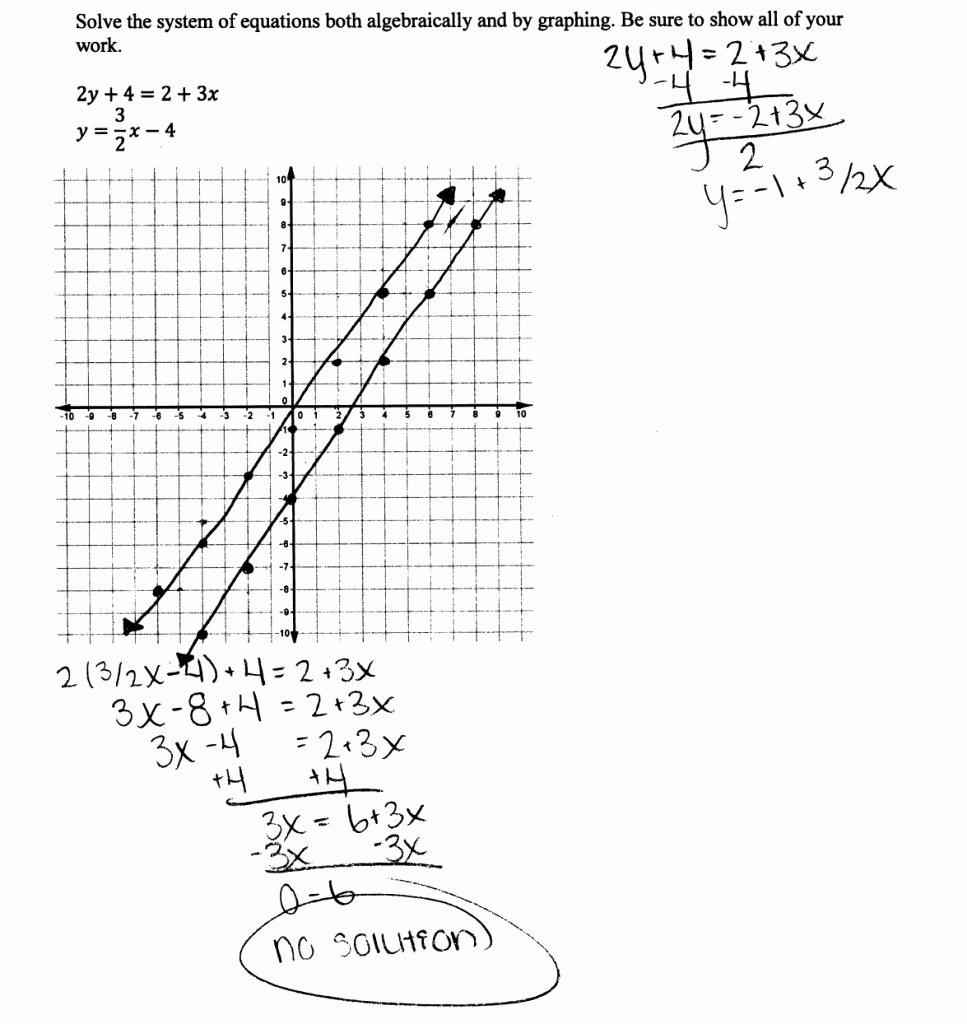
Solving Systems of Equations with Graphs

To solve systems:
- Graph Each Equation: Plot both equations on the same graph.
- Identify Intersections: The point where the graphs intersect represents the solution to the system. If lines don’t intersect, there is no solution. If lines overlap, there are infinite solutions.
Advanced Techniques in Equation Solving
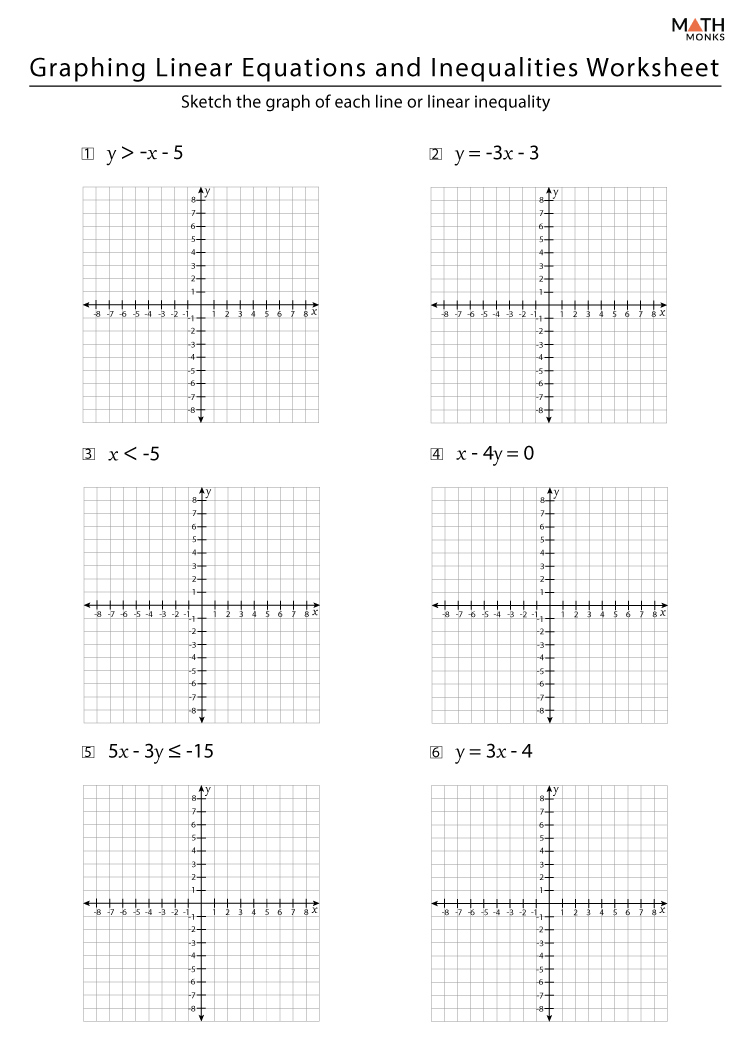
When dealing with higher-degree polynomials or trigonometric equations:
- Use of Calculators: Graphing calculators or online tools can help plot and solve complex equations.
- Substitution and Elimination: Algebraic methods can be used in conjunction with graphing to verify solutions.
🔍 Note: For some equations, graphing software or a calculator is essential to accurately visualize and solve.
Interpreting Graphs

Interpretation is key:
- Slope: Slope can tell us how steeply the line rises or falls. Positive slope means the graph is moving upwards, while negative indicates downward movement.
- Direction and Concavity: Understand the behavior of the curve, whether it opens up, down, or changes direction.
Real-World Applications

Graphing is not just academic; it’s practical:
- Economics: Graphing supply and demand curves to find equilibrium points.
- Physics: Understanding velocity and acceleration through distance-time graphs.
- Engineering: Designing systems where graphs can model structural behaviors or circuit design.
Having explored various aspects of graphing equations, it's clear that this technique isn't just about solving mathematical problems; it's about visualizing and understanding the mathematical world. Whether you're plotting a simple linear equation or dealing with more complex polynomials, the use of our Graphing Worksheet Guide helps translate abstract numbers into concrete, visual representations. This not only aids in problem-solving but also deepens your appreciation for the elegance and utility of mathematics. Now, when faced with equations, you'll have the tools to not only find solutions but also to comprehend their relationships, patterns, and real-world applications.
What are the benefits of using a Graphing Worksheet for solving equations?

+
Using a Graphing Worksheet can help visualize equations, making abstract concepts tangible, and allows you to identify patterns and solutions at a glance. It’s particularly useful for understanding how equations behave and interact with each other.
Can I solve complex equations without graphing?

+
Yes, many equations can be solved through algebraic methods, but graphing provides a visual verification or discovery of solutions that might not be immediately obvious through algebraic manipulation alone.
How can I use graphing to solve word problems?

+
Word problems often involve real-life scenarios which can be modeled with equations. By graphing these equations, you can visually find the solutions, intersect points, or critical values that answer the problem’s queries.



