Right Triangle Solutions: Worksheet Answers Revealed

In the world of geometry, right triangles hold a special place due to their practical applications in various fields, from architecture to engineering, physics, and even everyday scenarios like navigation. Understanding how to work with right triangles isn't just academic; it's a skill that can be highly beneficial in practical life. This post dives deep into solving problems related to right triangles, focusing particularly on providing worksheet answers to common questions students often encounter. Whether you're a student tackling geometry homework, a teacher looking for resources, or someone with a keen interest in mathematics, this detailed guide will serve you well.
Key Concepts for Solving Right Triangles
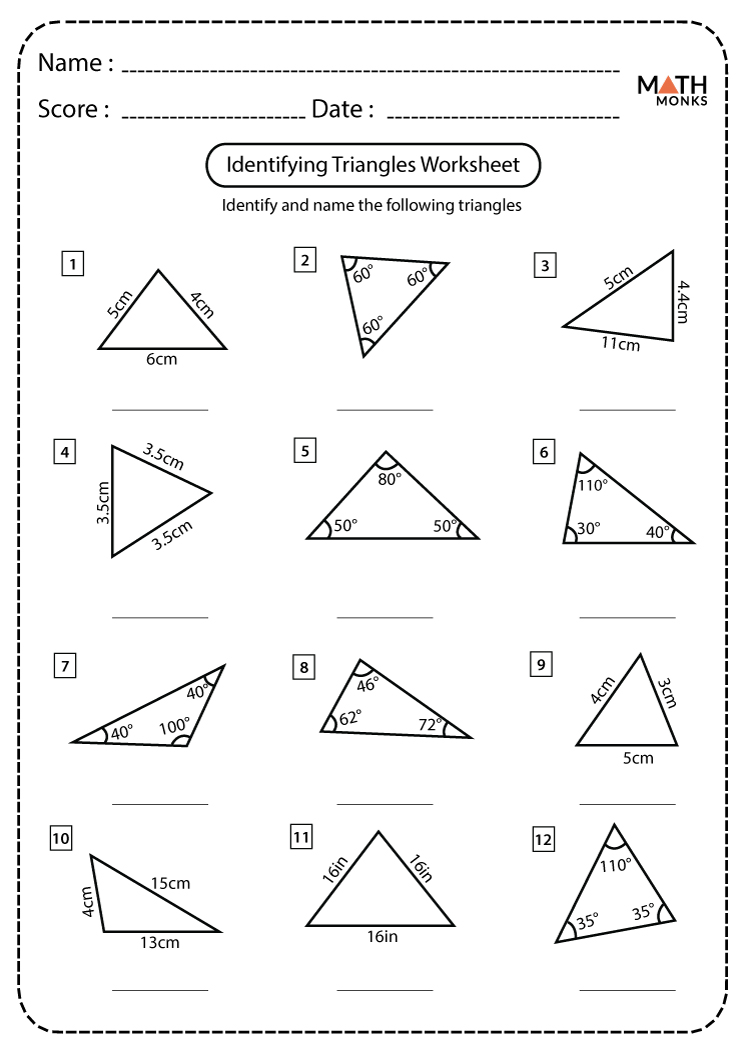
Before we delve into the solutions, let’s revise the core principles essential for working with right triangles:
- Pythagorean Theorem: If you know the lengths of two sides of a right triangle, you can find the length of the third side using the formula: (a^2 + b^2 = c^2), where (c) is the hypotenuse.
- Trigonometric Functions: Understanding sine (sin), cosine (cos), and tangent (tan) will allow you to find angles and side lengths when other information is available.
- Special Triangles: Familiarize yourself with the ratios of 45-45-90 and 30-60-90 triangles for quick problem-solving.
- Area of a Triangle: The area formula (A = \frac{1}{2} \times base \times height) is fundamental when dealing with right triangles.
Worksheet 1: Basic Calculations

Let’s start with simple problems focusing on the Pythagorean theorem:
Find the hypotenuse when the legs are 5 and 12.
Using (a^2 + b^2 = c^2), (5^2 + 12^2 = c^2).
(25 + 144 = c^2), so (c^2 = 169) and (c = \sqrt{169} = 13).
Find the length of one leg if the hypotenuse is 15 and the other leg is 9.
(a^2 + 9^2 = 15^2). Solving, we get (a = 12).
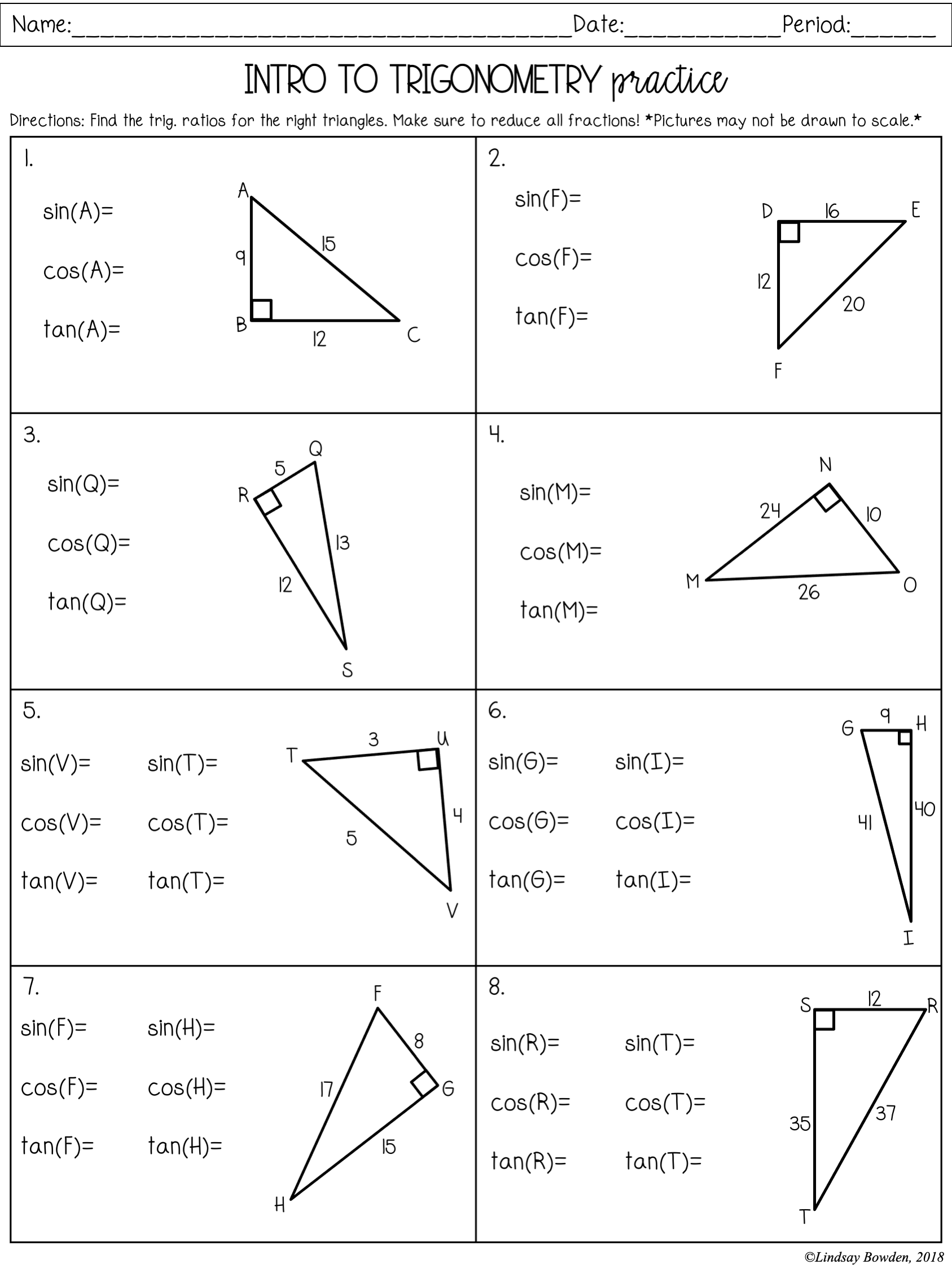
Worksheet 2: Applying Trigonometry

Here, we use sine, cosine, and tangent to find missing sides or angles:
Find the angle opposite the side of length 3 when the hypotenuse is 5.
Using (\sin(\theta) = \frac{opposite}{hypotenuse}), (\sin(\theta) = \frac{3}{5}).
(\theta = \sin^{-1}(0.6) \approx 36.87^\circ).
Find the length of the side adjacent to an angle of 30 degrees when the hypotenuse is 10.
Using (\cos(30^\circ) = \frac{adjacent}{hypotenuse}), (\cos(30^\circ) = \frac{adjacent}{10}).
(\frac{\sqrt{3}}{2} = \frac{adjacent}{10}) so (adjacent = 10 \times \frac{\sqrt{3}}{2} = 5\sqrt{3}).
Worksheet 3: Special Triangles
Let’s tackle problems involving special right triangles:
Find the length of the hypotenuse in a 45-45-90 triangle when one leg is 8.
In a 45-45-90 triangle, both legs are equal, and the hypotenuse is (\sqrt{2}) times the length of a leg:
The hypotenuse is (8\sqrt{2}).
Find the length of the shorter leg in a 30-60-90 triangle with a hypotenuse of 16.
In a 30-60-90 triangle, the hypotenuse is twice the length of the shorter leg:
The shorter leg is 8.
Applications in Real Life

Right triangles aren’t just a theoretical exercise; here are some practical applications:
- Construction: Builders use the Pythagorean theorem to ensure structures are square.
- Navigation: Pilots and sailors use trigonometry for distance and direction calculation.
- Land Surveying: Surveyors use right triangles to calculate distances and elevations.
To summarize, this blog post has walked you through the fundamental techniques for solving problems related to right triangles. We've covered basic Pythagorean theorem calculations, applied trigonometric functions, and worked with special triangles like the 45-45-90 and 30-60-90. Additionally, we've highlighted how these skills are not only useful in mathematics class but also have tangible real-world applications.
What is the Pythagorean theorem used for?

+
The Pythagorean theorem is used to find the length of one side of a right triangle when the lengths of the other two sides are known. It’s crucial in determining distances, like in surveying, construction, and navigation.
Why are special triangles important in trigonometry?

+
Special triangles, like the 45-45-90 and 30-60-90, have fixed ratios that allow for quick calculations of angles and sides, simplifying problems involving angles and proportions.
Can I use trigonometry only in a right triangle?

+
While trigonometry is most straightforward in right triangles, it can be applied to any triangle through the use of the law of sines and the law of cosines, extending its applications beyond just right triangles.
How do real-world problems use right triangles?

+
Right triangles are instrumental in fields like engineering for determining bridge spans, in architecture for creating right angles, and in navigation for calculating distances and heights. They also help in computer graphics for rendering 3D objects from 2D planes.
What are the key functions of trigonometry?

+
The key functions in trigonometry are sine (sin), cosine (cos), and tangent (tan). They are ratios of sides in a right triangle, allowing you to calculate angles and sides when some information is known.