Quadratic Equation Factoring Worksheet: Unveiling the Answers

The process of factoring quadratic equations can seem daunting at first, but it's a fundamental algebraic skill that, once mastered, opens up a plethora of mathematical problem-solving avenues. This blog post will guide you through the essence of quadratic equation factoring, offering clear examples, explanations, and a handy worksheet with answers to help solidify your understanding.
What are Quadratic Equations?
Quadratic equations are polynomial equations of degree 2, where the highest power of the variable is two. They’re commonly expressed in the standard form:
ax2 + bx + c = 0
- a: Coefficient of x2
- b: Coefficient of x
- c: Constant term
Why Factor Quadratic Equations?

Factoring is crucial for:
- Solving equations efficiently
- Understanding the behavior of the quadratic function
- Finding the roots or zeros of the polynomial
- Graphing functions more accurately
The Factoring Process

Here’s a step-by-step guide to factoring quadratic equations:
1. Identify the Quadratic Form

Ensure the equation is in the standard form, as shown above. If it isn’t, manipulate it into that form.
2. Look for Easy Factorizations

Check if the equation can be factored by looking for common factors or by trial and error with simple integers:
- If a = 1, factoring becomes simpler.
- Find two numbers whose product is ac and whose sum is b.
3. Rewrite the Middle Term

Once you’ve found these numbers, rewrite the middle term using them, then group and factor:
| Original Equation | Factored Form |
|---|---|
| ax2 + bx + c | (px + q)(rx + s) |

4. Factor by Grouping

Group the terms to create a structure that allows factoring out the common factors:
(a1x2 + b1x) + (b2x + c1) = (x + p)(x + q)
5. Check Your Work

Expand the factored form back to the original equation to ensure accuracy:
(x + p)(x + q) = x2 + (p+q)x + pq
🔎 Note: Remember to check for extraneous solutions when solving using these methods.
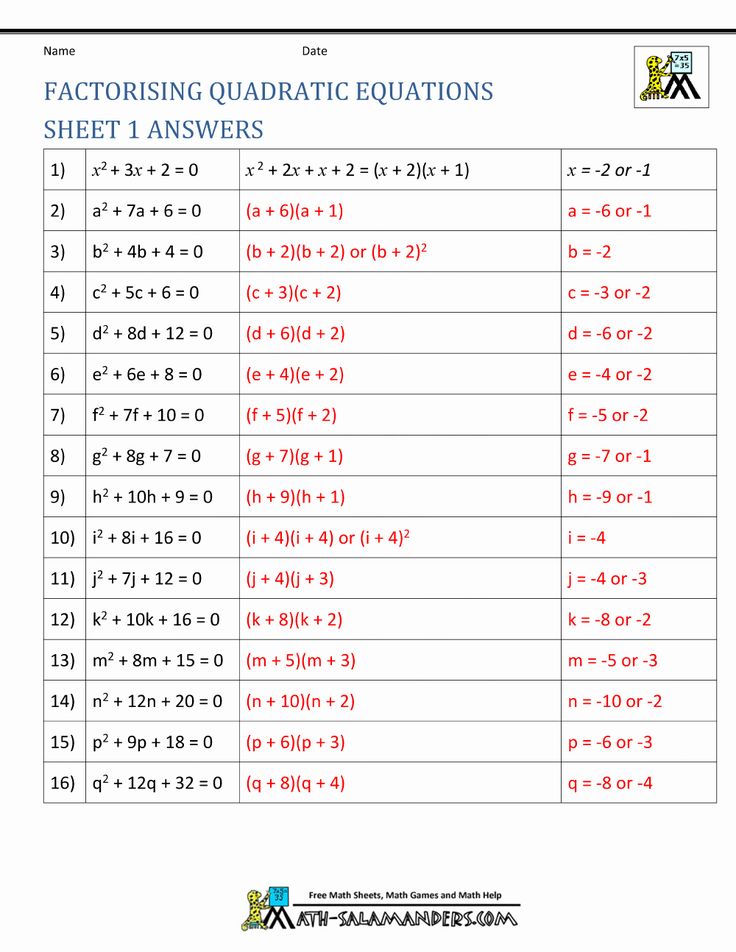
A Quadratic Factoring Worksheet with Answers

To reinforce what you’ve learned, here’s a worksheet to practice your factoring skills:
| Equation | Factored Form |
|---|---|
| x2 + 5x + 6 | (x + 2)(x + 3) |
| 2x2 + 7x + 6 | (2x + 3)(x + 2) |
| x2 - x - 6 | (x - 3)(x + 2) |
| 6x2 + x - 1 | (3x - 1)(2x + 1) |
📌 Note: Practicing with diverse examples helps in mastering the technique.
Understanding quadratic equation factoring is not just about solving specific equations but also about recognizing patterns and enhancing your algebraic fluency. This skill is critical in higher mathematics, physics, engineering, and many other fields where mathematical modeling plays a role. By working through the examples provided and applying the step-by-step process, you'll find that factoring becomes an intuitive and rewarding process.
What is the standard form of a quadratic equation?

+
The standard form of a quadratic equation is ax2 + bx + c = 0.
Why is factoring useful for solving quadratic equations?
+
Factoring helps in simplifying the equation, making it easier to solve for the roots or zeros, analyze the function’s behavior, and graph the function accurately.
Can all quadratic equations be factored?

+
Not all quadratic equations can be factored over the integers. Sometimes, the quadratic formula or completing the square might be necessary for solving.
What are some common mistakes when factoring quadratic equations?

+
Common mistakes include not checking for common factors, miscalculating the sum and product of the coefficients, and overlooking negative signs or factoring into the wrong binomials.
How can I ensure I’ve factored correctly?

+
Always expand your factored form to see if it matches the original equation, and check that your solutions satisfy the original equation.