5 Ways to Solve Quadratic Equations by Factoring

Introduction to Quadratic Equations by Factoring

Quadratic equations are a fundamental concept in algebra, and factoring is one of the most effective methods for solving them. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. In this blog post, we will explore five ways to solve quadratic equations by factoring.
Method 1: Factoring Quadratic Equations with Two Binomials

The first method involves factoring a quadratic equation into two binomials. This is the most common method of factoring, and it works by finding two numbers whose product is the constant term and whose sum is the coefficient of the x term.
For example, let’s factor the quadratic equation x^2 + 5x + 6 = 0.
🤔 Note: To factor this equation, we need to find two numbers whose product is 6 (the constant term) and whose sum is 5 (the coefficient of the x term). These numbers are 2 and 3.
We can rewrite the equation as (x + 2)(x + 3) = 0.
Steps to Factor a Quadratic Equation with Two Binomials:

- Write down the quadratic equation.
- Find two numbers whose product is the constant term and whose sum is the coefficient of the x term.
- Rewrite the equation as the product of two binomials.
Method 2: Factoring Quadratic Equations with the AC Method

The second method is known as the AC method. This method involves finding the factors of the product of the coefficients of the x^2 and constant terms.
For example, let’s factor the quadratic equation x^2 + 4x + 4 = 0.
🤔 Note: To factor this equation using the AC method, we need to find the factors of the product of the coefficients of the x^2 and constant terms. In this case, the product is 4 (the coefficient of the x^2 term) and 4 (the constant term).
We can rewrite the equation as (x + 2)(x + 2) = 0.
Steps to Factor a Quadratic Equation with the AC Method:

- Write down the quadratic equation.
- Find the factors of the product of the coefficients of the x^2 and constant terms.
- Rewrite the equation as the product of two binomials.
Method 3: Factoring Quadratic Equations by Grouping

The third method involves grouping the terms of the quadratic equation to factor it.
For example, let’s factor the quadratic equation x^2 + 3x + 2 = 0.
🤔 Note: To factor this equation by grouping, we need to group the terms into two pairs: x^2 + 3x and 2.
We can rewrite the equation as (x + 1)(x + 2) = 0.
Steps to Factor a Quadratic Equation by Grouping:

- Write down the quadratic equation.
- Group the terms into two pairs.
- Factor each pair separately.
- Rewrite the equation as the product of two binomials.
Method 4: Factoring Quadratic Equations with a Difference of Squares

The fourth method involves factoring a quadratic equation with a difference of squares. This method works by recognizing that a quadratic equation with a difference of squares can be factored into the product of two binomials.
For example, let’s factor the quadratic equation x^2 - 4 = 0.
🤔 Note: To factor this equation, we can recognize that it is a difference of squares: x^2 - 4 = (x - 2)(x + 2) = 0.
Steps to Factor a Quadratic Equation with a Difference of Squares:

- Write down the quadratic equation.
- Recognize that the equation is a difference of squares.
- Factor the equation into the product of two binomials.
Method 5: Factoring Quadratic Equations with a Perfect Square Trinomial

The fifth method involves factoring a quadratic equation with a perfect square trinomial. This method works by recognizing that a quadratic equation with a perfect square trinomial can be factored into the square of a binomial.
For example, let’s factor the quadratic equation x^2 + 6x + 9 = 0.
🤔 Note: To factor this equation, we can recognize that it is a perfect square trinomial: x^2 + 6x + 9 = (x + 3)^2 = 0.
Steps to Factor a Quadratic Equation with a Perfect Square Trinomial:

- Write down the quadratic equation.
- Recognize that the equation is a perfect square trinomial.
- Factor the equation into the square of a binomial.
In conclusion, there are several methods to solve quadratic equations by factoring. Each method has its own strengths and weaknesses, and the choice of method depends on the specific equation being solved. By mastering these methods, you can become proficient in solving quadratic equations by factoring.
What is a quadratic equation?
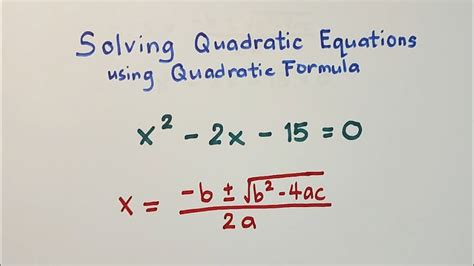
+
A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two.
What is factoring in algebra?

+
Factoring in algebra involves expressing an algebraic expression as the product of simpler expressions.
What are the five methods of solving quadratic equations by factoring?

+
The five methods are: (1) factoring with two binomials, (2) the AC method, (3) factoring by grouping, (4) factoring with a difference of squares, and (5) factoring with a perfect square trinomial.



