Solving One and Two Step Inequalities: Free Worksheet
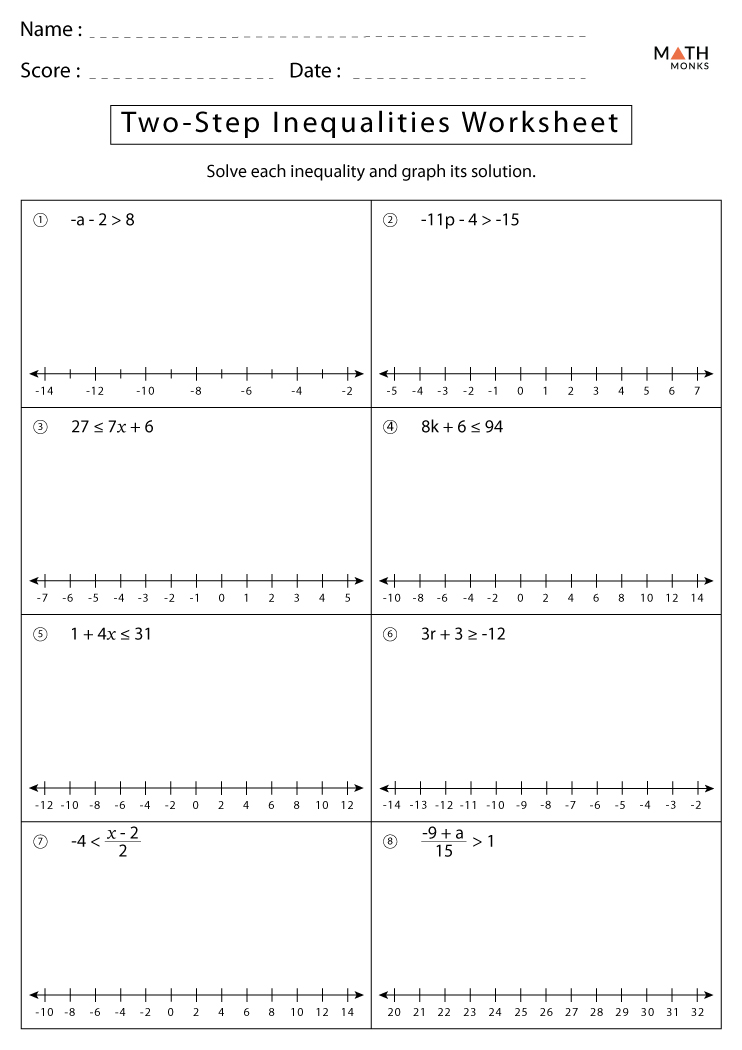
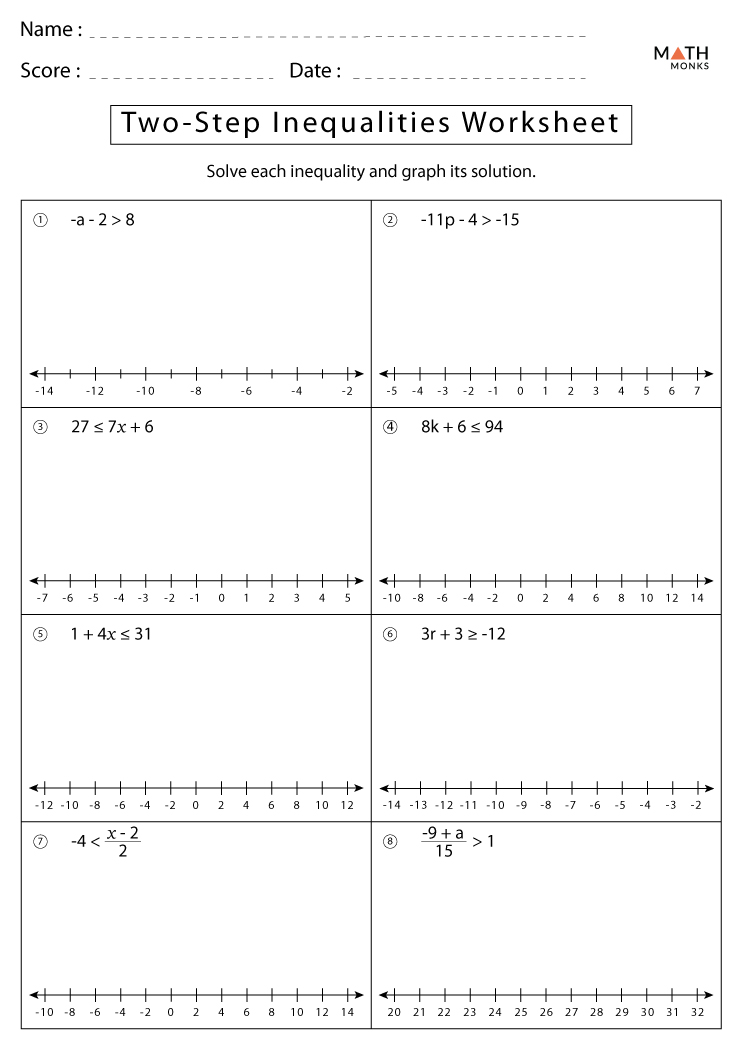
Mastering the skill of solving inequalities is crucial for students who are navigating through algebra. This blog post delves into the methods for tackling one and two-step inequalities, providing not only clear instructions but also a free worksheet to practice what you've learned. By understanding the steps, students can confidently move forward in their mathematical education.
Understanding Inequalities

Before we dive into solving inequalities, let's clarify what an inequality is. An inequality shows a relationship between two values where one is less than, greater than, less than or equal to, or greater than or equal to the other. These relationships can be symbolized as follows:
- < : Less than
- > : Greater than
- ≤ : Less than or equal to
- ≥ : Greater than or equal to
Understanding these symbols is vital as they dictate how to approach the inequalities.
Solving One-Step Inequalities
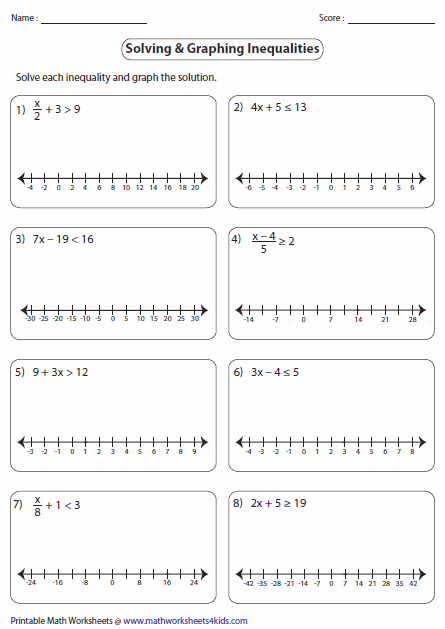
One-step inequalities are solved in a single operation, similar to solving one-step equations:
- Add/Subtract: If the variable term is accompanied by a constant, simply add or subtract this constant from both sides to isolate the variable.
- Multiply/Divide: If the variable term is multiplied or divided by a number, perform the opposite operation to isolate the variable. Remember to flip the inequality sign if you multiply or divide by a negative number.
Here's an example:
| Example | Step-by-Step Solution |
|---|---|
| x + 3 > 7 |
|

Image


🔍 Note: Flipping the inequality sign when multiplying or dividing by a negative number maintains the truth of the statement.
Solving Two-Step Inequalities

Two-step inequalities require two operations to isolate the variable:
- Add or Subtract to move the constant to one side.
- Multiply or Divide to remove the coefficient from the variable, adjusting the inequality if necessary.
Here’s how you can do it:
| Example | Step-by-Step Solution |
|---|---|
| 2x + 6 ≤ 12 |
|
Image

⚠️ Note: The same rule for sign flipping applies to two-step inequalities when dealing with negative coefficients.
Key Tips:
- Read Carefully: Always read the inequality twice to ensure you understand the relationship.
- Manipulate Both Sides: Any operation done to one side must also be done to the other to maintain the inequality.
- Check Solutions: Verify solutions by substituting them back into the original inequality.
In summary, understanding how to solve one and two-step inequalities is fundamental for students. By practicing with the free worksheet provided, you can enhance your ability to isolate variables and understand the conditions under which inequalities hold true. This practice not only builds confidence but also prepares you for more complex algebraic tasks in the future.
What is the difference between an equation and an inequality?

+
An equation asserts that two expressions are equal, while an inequality compares two expressions indicating a relationship of more or less.
Why do we flip the inequality sign when multiplying or dividing by a negative number?
+
The inequality sign flips to keep the direction of the inequality correct when the numbers are switched in their relationship to zero.
Can inequalities have no solution or multiple solutions?

+
Yes, inequalities can have no solution if the statement is always false (e.g., x < 2 and x > 5) or infinite solutions if the inequality is always true (e.g., x + 3 > x).