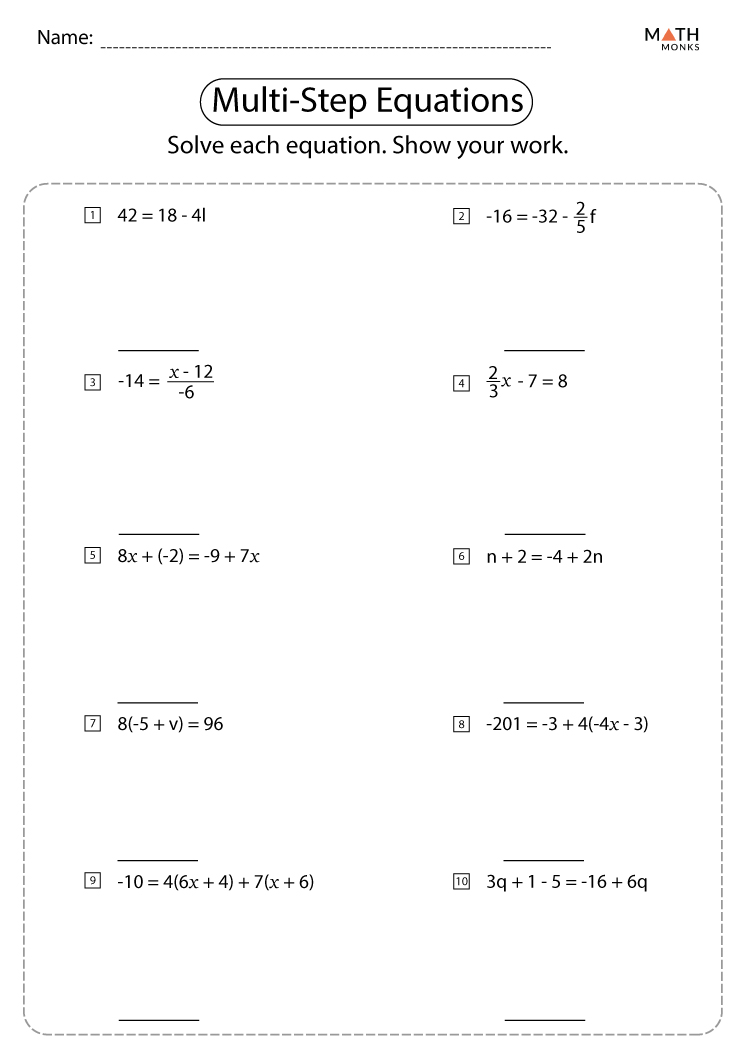
Multi-Step Equations Algebra 1 Worksheet Solutions
In this detailed guide, we'll walk you through how to solve multi-step equations, a crucial skill for algebra students to master. Understanding these equations not only helps in solving basic math problems but also forms a foundation for advanced math concepts. Here's how you can effectively tackle these equations:
Step 1: Simplifying Both Sides of the Equation

The first step in solving multi-step equations is to simplify both sides to make the equation easier to solve. Here are the actions you should take:
- Combine like terms, if any are present on either side.
- Distribute through parentheses or brackets where necessary.
- Move constants or terms without variables to one side, if beneficial.
Here’s an example to illustrate:
Solve: 5x + 3 - x = 2x + 8 Combine like terms on the left side: 4x + 3 = 2x + 8
Step 2: Isolate the Variable

Once you’ve simplified both sides, the goal is to get all variable terms on one side and constant terms on the other. Here’s what to do:
- Decide which side you want the variable to be on.
- Move the terms by adding or subtracting the variable or constant terms from both sides.
Continuing the example:
Move terms to isolate x: 4x - 2x = 8 - 3 2x = 5
Step 3: Solve for the Variable

Now that the variable is isolated, solve for its value:
- Divide both sides of the equation by the coefficient of x.
Our example:
Divide both sides by 2: x = 5/2
🔍 Note: Always check your solution by substituting it back into the original equation to ensure it works.
Step 4: Verify the Solution

Verification is essential to confirm that your solution is correct:
- Substitute the solution back into the original equation.
- Simplify both sides to ensure they are equal.
Let’s verify:
Substitute x = 5/2 into the original equation: 5(5/2) + 3 - (5/2) = 2(5/2) + 8 Simplify: (25/2) + 3 - (5/2) = (10/2) + 8 (25 - 5)/2 + 3 = 5 + 8 20/2 + 3 = 13 10 + 3 = 13 13 = 13
This confirms our solution is correct.
Using Tables for Solving Equations

Here’s a table to help visualize the process:
| Step | Operation | Equation |
|---|---|---|
| 1 | Combine like terms | 5x + 3 - x = 2x + 8 → 4x + 3 = 2x + 8 |
| 2 | Move variable to one side | 4x - 2x = 8 - 3 → 2x = 5 |
| 3 | Divide by coefficient | 2x / 2 = 5 / 2 → x = 5⁄2 |
| 4 | Verify solution | Substitute back and simplify: 13 = 13 |

✏️ Note: Using tables can provide a structured way to visualize each step in solving equations, making the process more digestible.
In wrapping up this guide, mastering multi-step equations involves understanding and applying each step: simplifying, isolating, solving, and verifying. This process not only ensures that you can solve equations accurately but also prepares you for more complex algebraic challenges. Whether for daily math problems or advanced calculus, these skills are indispensable.
What are multi-step equations?

+
Multi-step equations require more than one operation to solve for the variable. They often involve variables on both sides of the equation, requiring distribution, combining like terms, and isolating the variable.
Why is verifying the solution important?

+
Verifying the solution ensures that your solution is correct by substituting it back into the original equation. This step helps catch any mistakes made during the solving process.
Can I skip the verification step?

+
It’s not advisable. Although you might be confident in your solution, verifying helps ensure accuracy, especially in more complex equations where errors can easily occur.