Mastering Multi Step Equations Worksheet for Algebra Success

Unlocking the Secrets of Multi-Step Equations

Multi-step equations are a fundamental concept in algebra, and mastering them is crucial for success in math and science. In this comprehensive guide, we’ll delve into the world of multi-step equations, exploring their definition, types, and step-by-step solutions. By the end of this tutorial, you’ll be equipped with the skills and confidence to tackle even the most complex equations.
What are Multi-Step Equations?

Multi-step equations are algebraic expressions that require more than one step to solve. They involve a combination of addition, subtraction, multiplication, and division operations, making them more challenging than simple one-step equations. These equations are commonly used to model real-world problems, such as physics, engineering, and economics.
Types of Multi-Step Equations

There are several types of multi-step equations, including:
- Linear Equations: These equations involve a single variable and can be solved using addition, subtraction, multiplication, and division.
- Quadratic Equations: These equations involve a squared variable and can be solved using factoring, quadratic formula, or graphing.
- Rational Equations: These equations involve fractions and can be solved using algebraic manipulations.
Step-by-Step Solution to Multi-Step Equations

To solve multi-step equations, follow these steps:
- Simplify the Equation: Combine like terms, eliminate any parentheses, and rewrite the equation in a simplified form.
- Isolate the Variable: Use addition, subtraction, multiplication, and division to isolate the variable on one side of the equation.
- Use Algebraic Properties: Apply algebraic properties, such as the distributive property, to simplify the equation.
- Check the Solution: Plug the solution back into the original equation to ensure it’s true.
📝 Note: Always follow the order of operations (PEMDAS) when simplifying and solving multi-step equations.
Examples of Multi-Step Equations
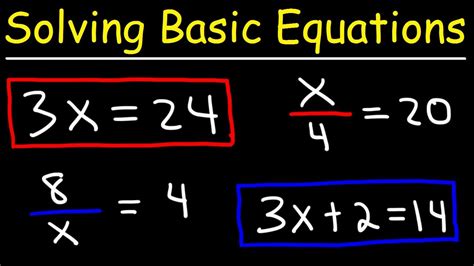
Let’s work through some examples to illustrate the step-by-step solution process:
Example 1: Solve for x in the equation 2x + 5 = 11.
- Simplify the equation: 2x + 5 = 11
- Isolate the variable: 2x = 11 - 5
- Use algebraic properties: 2x = 6
- Solve for x: x = 6 ÷ 2
- Check the solution: 2(3) + 5 = 11 (True)
Example 2: Solve for y in the equation y - 3 = 7.
- Simplify the equation: y - 3 = 7
- Isolate the variable: y = 7 + 3
- Use algebraic properties: y = 10
- Check the solution: 10 - 3 = 7 (True)
Common Mistakes to Avoid

When solving multi-step equations, beware of these common mistakes:
- Incorrect Order of Operations: Make sure to follow the order of operations (PEMDAS) when simplifying and solving equations.
- Incorrect Signs: Pay attention to the signs of the variables and constants, as incorrect signs can lead to incorrect solutions.
- Insufficient Simplification: Simplify the equation thoroughly before isolating the variable.
Practicing Multi-Step Equations

Practice is key to mastering multi-step equations. Try solving these exercises:
| Equation | Solution |
|---|---|
| 3x + 2 = 14 | x =? |
| 2y - 4 = 12 | y =? |
| x/2 + 3 = 5 | x =? |

📝 Note: Check your solutions to ensure they're true.
By following these steps and practicing regularly, you’ll become proficient in solving multi-step equations and unlock the secrets of algebra.
What is the main difference between one-step and multi-step equations?
+
One-step equations involve a single operation, whereas multi-step equations require multiple operations to solve.
How do I know which operation to perform first when solving a multi-step equation?

+
Follow the order of operations (PEMDAS) to ensure you perform the correct operations in the correct order.
What is the best way to practice solving multi-step equations?

+
Practice regularly, using a variety of equations and exercises, and check your solutions to ensure they’re true.