5 Tips for Mastering Inequality Problems

Are you struggling with inequality problems in mathematics? Whether you're a student gearing up for an exam or an enthusiast looking to refine your math skills, mastering inequalities can be quite rewarding. This comprehensive guide offers 5 tips for mastering inequality problems that will help you understand, solve, and even enjoy these math challenges.
1. Understanding the Basics of Inequalities


Inequalities compare two values where one value might not be equal to the other. Here’s a quick overview:
- Greater Than (>) : e.g., ( x > 3 )
- Greater Than or Equal To (≥) : e.g., ( y ≥ 2 )
- Less Than (<) : e.g., ( a < 5 )
- Less Than or Equal To (≤) : e.g., ( b ≤ 7 )
- Not Equal To (≠) : e.g., ( m ≠ n )
⚠️ Note: Keep in mind that when solving inequalities, the direction of the inequality sign can change when both sides are multiplied or divided by a negative number.
2. Simplify and Solve


The goal in solving inequalities is similar to solving equations: isolate the variable on one side. Here’s how:
- Combine like terms.
- Eliminate any fractions or decimals if possible.
- Move all terms containing the variable to one side and constants to the other.
- Perform the arithmetic to solve for the variable.
💡 Note: Always keep track of the operations you perform; you may need to reverse them to check your work.
3. Graphical Approach


Graphing inequalities provides a visual representation which can be incredibly helpful:
- Open Circle: Use for ( > ) or ( < ), indicating that the solution does not include the point.
- Closed Circle: Use for ( ≥ ) or ( ≤ ), indicating the solution includes the point.
- Graph the line that represents the equality part, then shade the appropriate area based on the inequality sign.
🌟 Note: Use graph paper or a graphing calculator for accuracy; hand-drawn graphs can sometimes lead to small inaccuracies.
4. System of Inequalities


When dealing with multiple inequalities simultaneously, follow these steps:
- Graph each inequality separately on the coordinate plane.
- The solution set will be the overlapping regions where all the inequalities are satisfied.
- Identify and test points from these regions to ensure they fulfill all the inequalities.
📝 Note: Remember to test points that are on the boundaries of these regions as well, especially for cases involving equalities (≥, ≤).
5. Practice and Application
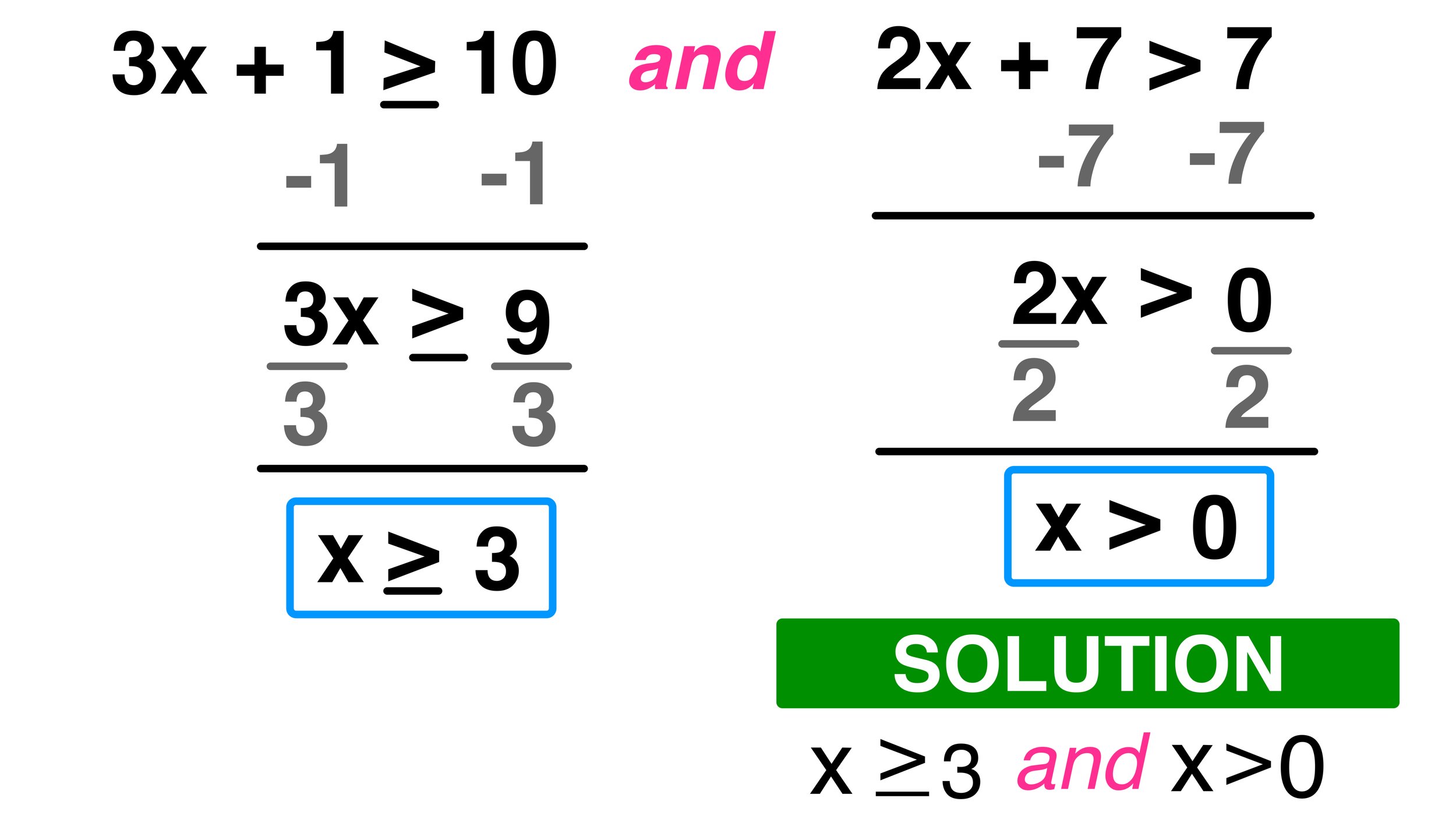

Lastly, nothing beats practice:
- Engage with real-world problems where inequalities apply, like budgeting or optimization problems.
- Solve various types of inequalities regularly to keep your skills sharp.
- Use online tools or software for interactive practice sessions.
To sum it all up, mastering inequalities requires a strong foundation in understanding the basic concepts, applying simplification techniques, using graphical methods for visualization, tackling systems of inequalities, and continually practicing through real-world and theoretical problems. With these strategies in your toolkit, inequalities become not just understandable but also enjoyable to solve.
Why do inequalities sometimes require changing the direction of the sign?

+
When you multiply or divide both sides of an inequality by a negative number, the inequality sign must be flipped to maintain the truth of the statement.
How can you tell if an inequality should have an open or closed circle when graphing?

+
If the inequality is strict (> or <), use an open circle to show the value is not included. If the inequality is inclusive (≥ or ≤), use a closed circle to indicate the value is included.
What is the significance of using graphical methods for inequalities?

+
Graphical methods visually represent the solution sets of inequalities, which can make it easier to understand and solve systems of inequalities by identifying the overlapping areas that satisfy all conditions.