5 Steps to Solve Inequalities Easily

Introduction to Solving Inequalities

When students encounter mathematics, they often find solving inequalities to be a challenging task. However, with a few structured steps and the right mindset, mastering inequalities can become an enjoyable part of your math journey. In this post, we’ll break down inequalities into five manageable steps, ensuring you can approach them with confidence and ease.
Step 1: Understand the Basics of Inequalities

Before diving into solving inequalities, it’s crucial to grasp what they represent. An inequality shows a relationship where two quantities can be unequal. Here’s what you need to know:
- < less than
- > greater than
- ≤ less than or equal to
- ≥ greater than or equal to
📘 Note: Unlike equations, where the goal is to find an exact value, inequalities give you a range of values where the statement remains true.
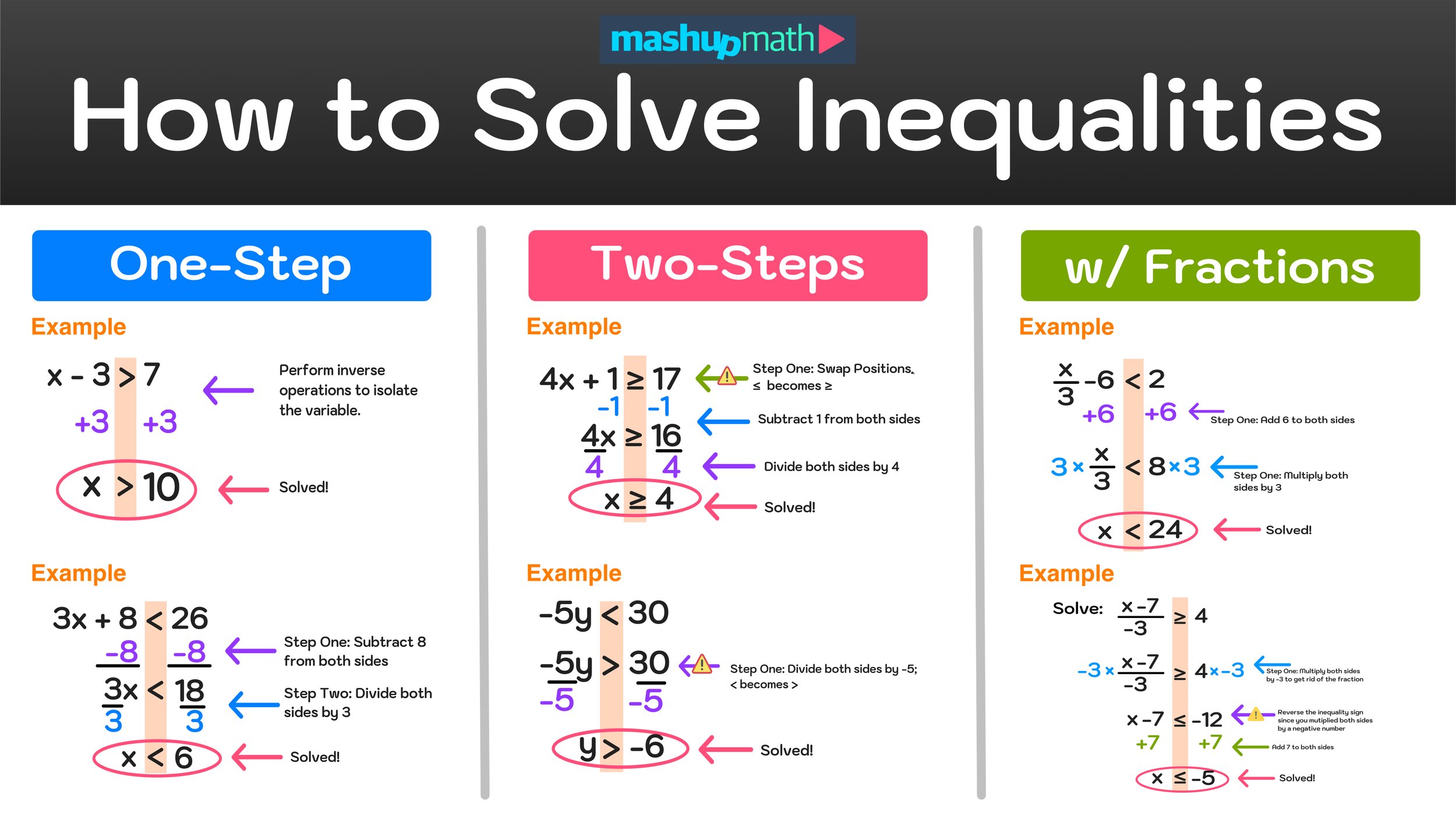
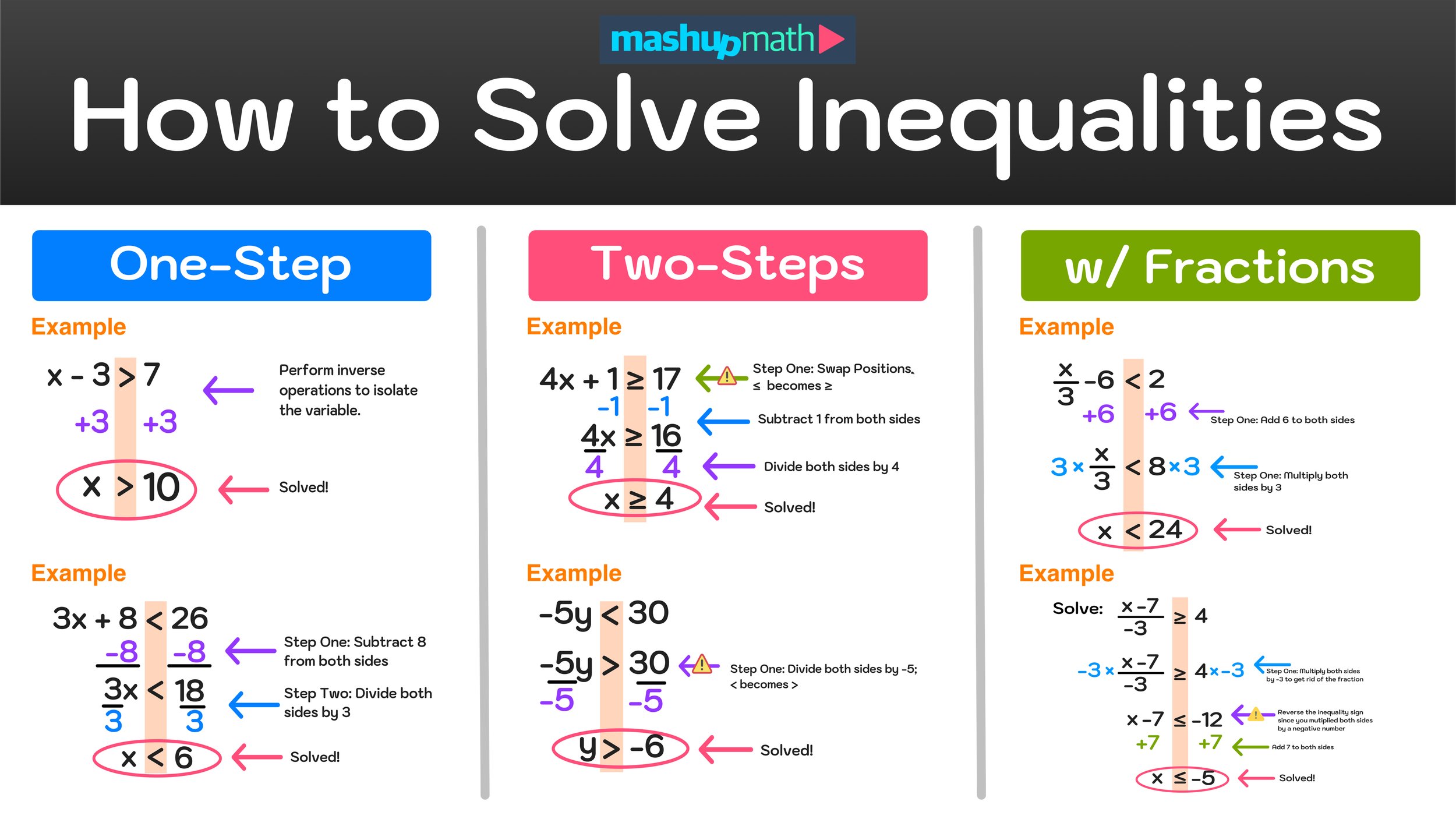
Step 2: Simplify the Inequality

Like any algebraic expression, you might need to simplify your inequality. Here’s how:
- Eliminate any like terms on both sides of the inequality.
- Combine constants to make the problem more manageable.
- Distribute any multiplication or division operations correctly.
For instance, simplify 3x + 2 > 14 by subtracting 2 from both sides to get 3x > 12.
Step 3: Isolate the Variable

The goal is to get the variable alone on one side of the inequality. Here are the key actions:
- Move all constants to the other side of the inequality.
- If there’s a coefficient with the variable, divide or multiply both sides to eliminate it.
From our example, divide both sides by 3 to isolate x, giving us x > 4.
Step 4: Solve for the Variable

Now that your variable is isolated, you have the solution. Here are some tips:
- Remember that if you multiply or divide by a negative number, you must flip the inequality sign.
- Double-check your work to ensure all steps were applied correctly.
Step 5: Plot the Solution on a Number Line

Visualizing the solution helps understand the range of values where the inequality holds true:
- Use an open or closed circle for the boundary point depending on whether the inequality includes or excludes that point.
- Draw an arrow in the direction where the values should be.
Here's how you might represent x > 4 on a number line:
| Number Line | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Plot | ○ | → | → |
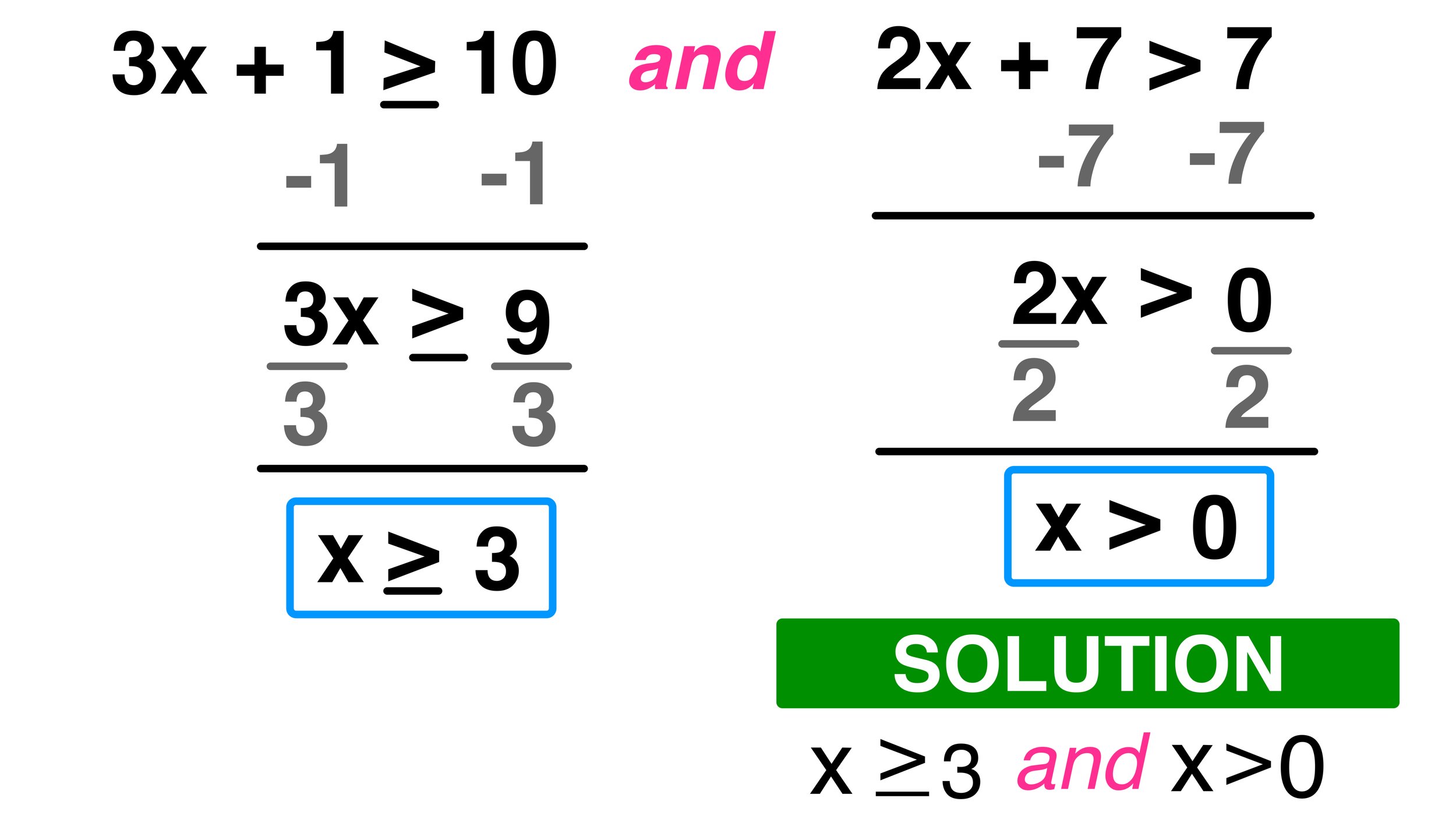
📝 Note: Plotting on a number line helps visualize inequalities, especially when dealing with compound inequalities.
Final Thoughts

Solving inequalities, while initially daunting, becomes a breeze with these steps. From understanding the basics to visualizing solutions, each stage builds upon the last, providing a clear, logical approach to tackle any inequality. Practice these steps, and soon you’ll find that inequalities reveal not just answers but a deeper understanding of algebraic concepts.
What are the most common mistakes when solving inequalities?
+
The most common mistakes include forgetting to reverse the inequality sign when multiplying or dividing by a negative number and not simplifying the inequality properly before isolating the variable.
Can I solve inequalities without plotting them on a number line?
+
Yes, you can solve inequalities without a number line. However, plotting helps visualize the solution and understand the range of values where the inequality holds.
Are there different methods to solve inequalities?

+
There are several methods, including algebraic manipulation, graphical methods, and substitution, but the steps outlined here provide a structured approach to most inequalities you’ll encounter.