Mastering Inequalities and Equations: Free Worksheet Guide

When diving into the world of mathematics, particularly algebra, one of the most foundational skills to master is working with inequalities and equations. These concepts are not just tools for solving academic problems but are also crucial in various real-world applications ranging from economics, engineering, to computer science. This blog post provides a comprehensive guide to inequalities and equations through an extensive free worksheet that you can download, designed to challenge and sharpen your problem-solving abilities. Let's delve deep into this fascinating journey.
Understanding Inequalities and Equations

Inequalities and equations both serve as the language of mathematics, allowing us to express relationships between quantities. Here’s how they differ:
- Equations: When two expressions are equal. The goal is to find the value(s) of the variable(s) that make the equation true.
- Inequalities: When two expressions are compared using symbols like <, >, ≤, ≥ or ≠. These indicate that one expression is less than, greater than, less than or equal to, greater than or equal to, or not equal to another expression.
Why They Matter
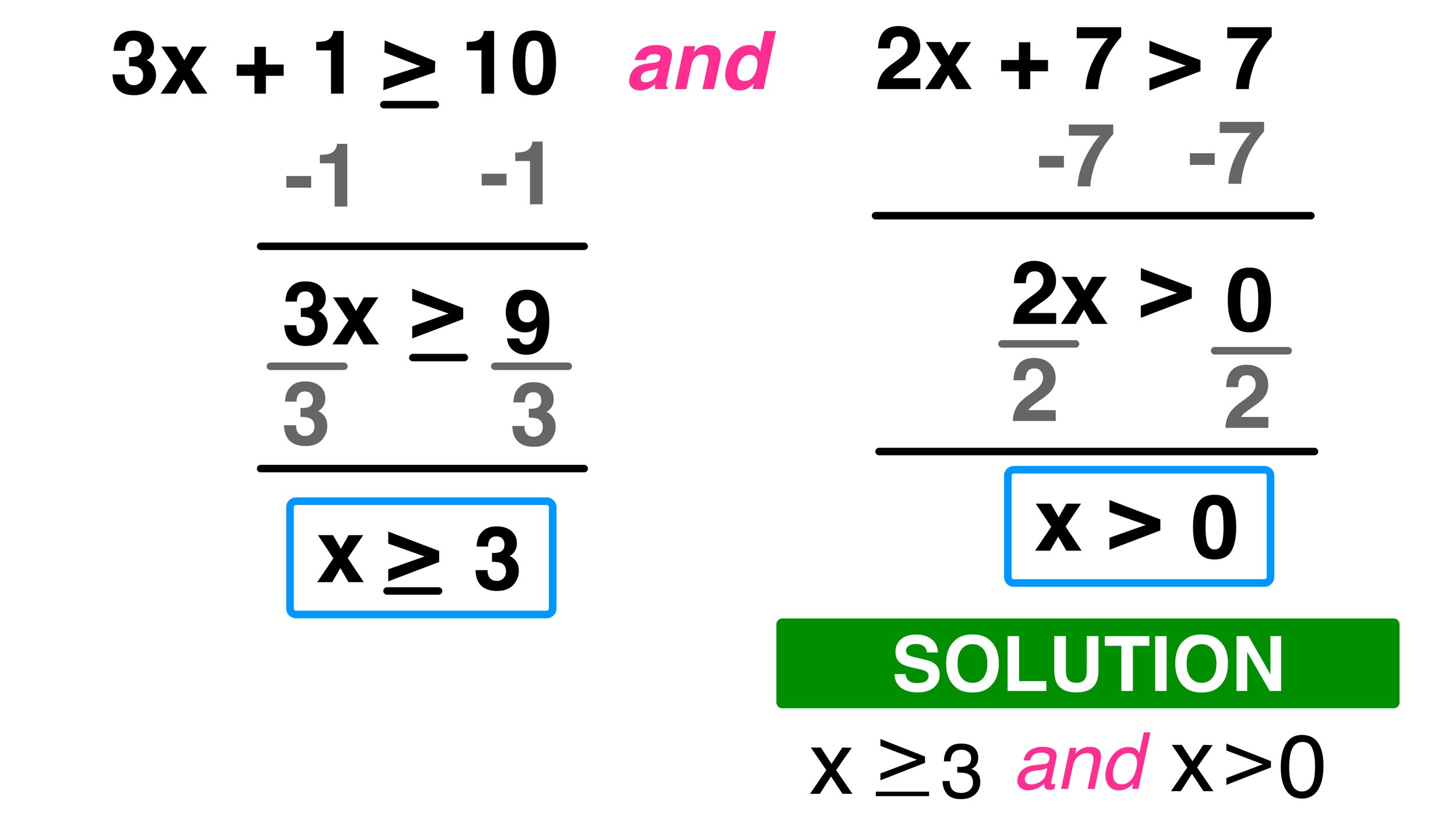
Inequalities and equations are not merely abstract mathematical constructs. They are practical tools for:
- Setting boundaries and constraints in optimization problems.
- Solving systems to predict behaviors in economics and physics.
- Formulating logical conditions in computer programming.
- Calculating profit margins, costs, and other business-related metrics.
Free Worksheet Overview

The Mastering Inequalities and Equations: Free Worksheet Guide includes a range of problems that:
- Cover linear, quadratic, and polynomial inequalities.
- Challenge you with absolute value and system of equations and inequalities.
- Offer graphical representation problems to visualize solutions.
- Include word problems to apply math to real-life scenarios.
Key Concepts

Linear Inequalities

Linear inequalities are straightforward but fundamental. Here, we discuss how to:
- Isolate the variable by performing algebraic operations.
- Use the sign rule: multiply or divide both sides by a negative number, flip the inequality sign.
🔑 Note: While solving inequalities, remember to reverse the inequality sign when you multiply or divide by a negative number.
Quadratic Inequalities

Quadratic inequalities introduce a second-degree polynomial, requiring you to:
- Solve the corresponding quadratic equation to find critical points.
- Use these points to partition the real line into intervals.
- Test each interval to determine where the inequality holds true.
Polynomial Inequalities

Similar to quadratic, polynomial inequalities involve:
- Finding critical points by solving the polynomial equation.
- Partitioning the real line and testing the sign of the polynomial in each interval.
Absolute Value Inequalities

Handling absolute value inequalities demands:
- Transforming the absolute value inequality into two separate inequalities.
- Solving each resulting inequality separately.
System of Equations and Inequalities

Systems combine multiple equations or inequalities, requiring:
- Graphing the lines or regions to visualize the solution space.
- Identifying the intersection points or common regions for solutions.
After working through these examples, your understanding of how to manipulate inequalities and equations will be significantly bolstered.
Download and Use

To download the Mastering Inequalities and Equations: Free Worksheet, simply click on the link provided below:
- The worksheet is organized by difficulty, from basic to advanced.
- Each section comes with example solutions to guide you through the problem-solving process.
- Space for notes and hints to help you navigate through complex problems.
Benefits of Using the Worksheet

By engaging with this worksheet, you’ll:
- Strengthen your ability to analyze and solve problems.
- Develop a deeper understanding of algebraic manipulation techniques.
- Gain confidence in tackling real-world applications of math.
- Enhance your preparation for competitive exams or algebra courses.
In summary, this guide and accompanying worksheet provide an exhaustive exploration into inequalities and equations, empowering you with the knowledge and skills to handle these mathematical tools with ease and precision. Applying these concepts to practical problems and mastering these foundational elements of algebra will not only bolster your academic prowess but also equip you with problem-solving capabilities for real-world challenges.
What are some common mistakes in solving inequalities?

+
Common mistakes include forgetting to reverse the inequality sign when multiplying or dividing by a negative number, neglecting to consider all possible solutions when dealing with absolute values, and failing to test intervals correctly in polynomial inequalities.
How can I improve my skills in working with inequalities?

+
Practice regularly with a variety of problems. Focus on understanding the underlying concepts rather than just memorizing steps. Visualize solutions through graphing when possible, and always check your work against the original problem.
Why are systems of equations important in real-life applications?

+
Systems of equations model real-world problems where multiple conditions must be satisfied simultaneously. They are used in optimization, resource allocation, and predicting outcomes based on different variables interacting with one another.
Can you solve inequalities with variables on both sides?
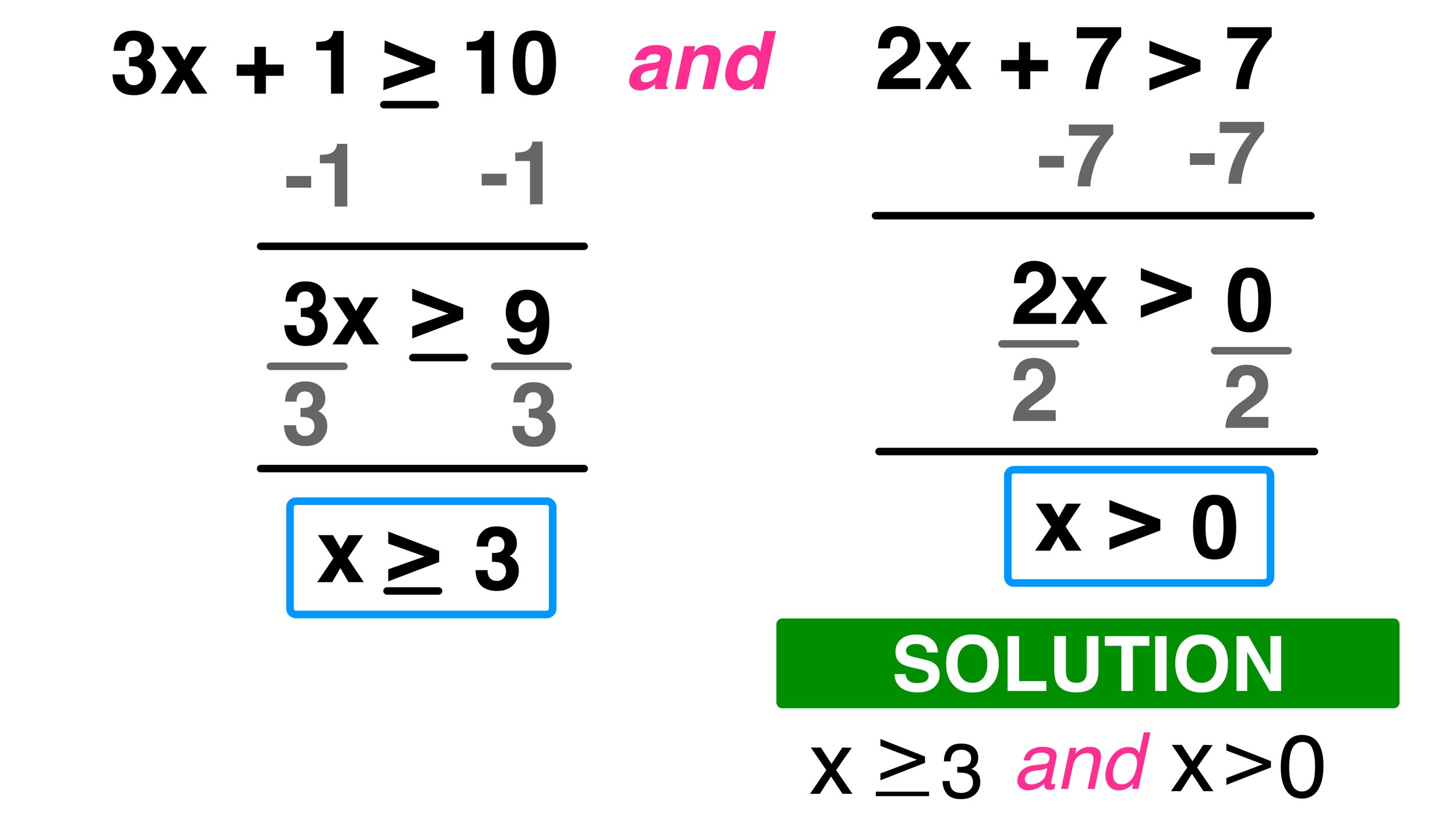
+
Absolutely! The process involves isolating the variable on one side, maintaining the inequality sign by applying algebraic operations equally to both sides. Remember to reverse the sign when dividing or multiplying by a negative number.
How do quadratic inequalities differ from linear inequalities?

+
Quadratic inequalities involve a second-degree polynomial, resulting in potentially two solution intervals due to the parabolic nature of the curve. Linear inequalities have linear expressions leading to one continuous solution interval, with direction determined by the inequality sign.