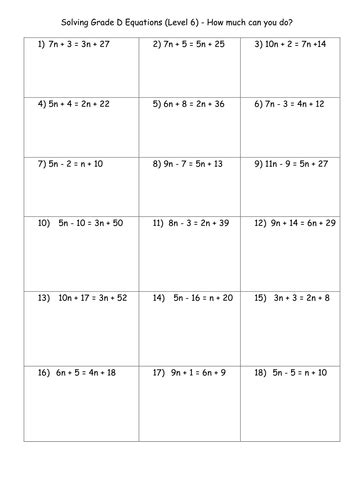
Solving Equations With X On Both Sides Worksheet

Solving Equations with X on Both Sides: A Step-by-Step Guide

When solving equations with variables on both sides, it’s essential to apply the rules of algebra to isolate the variable. In this post, we’ll explore how to solve equations with X on both sides, providing a comprehensive guide with examples and exercises to help you master this concept.
Understanding the Basics

Before diving into solving equations with X on both sides, let’s review the fundamental rules of algebra:
- The commutative property states that the order of the numbers or variables does not change the result of the operation.
- The associative property states that the order in which we perform operations does not affect the result.
- The distributive property allows us to distribute a single term across the terms inside parentheses.
These properties will be crucial in solving equations with X on both sides.
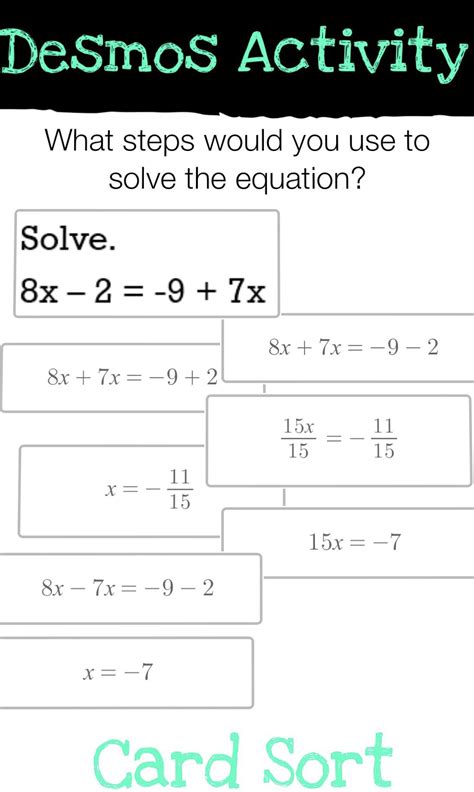
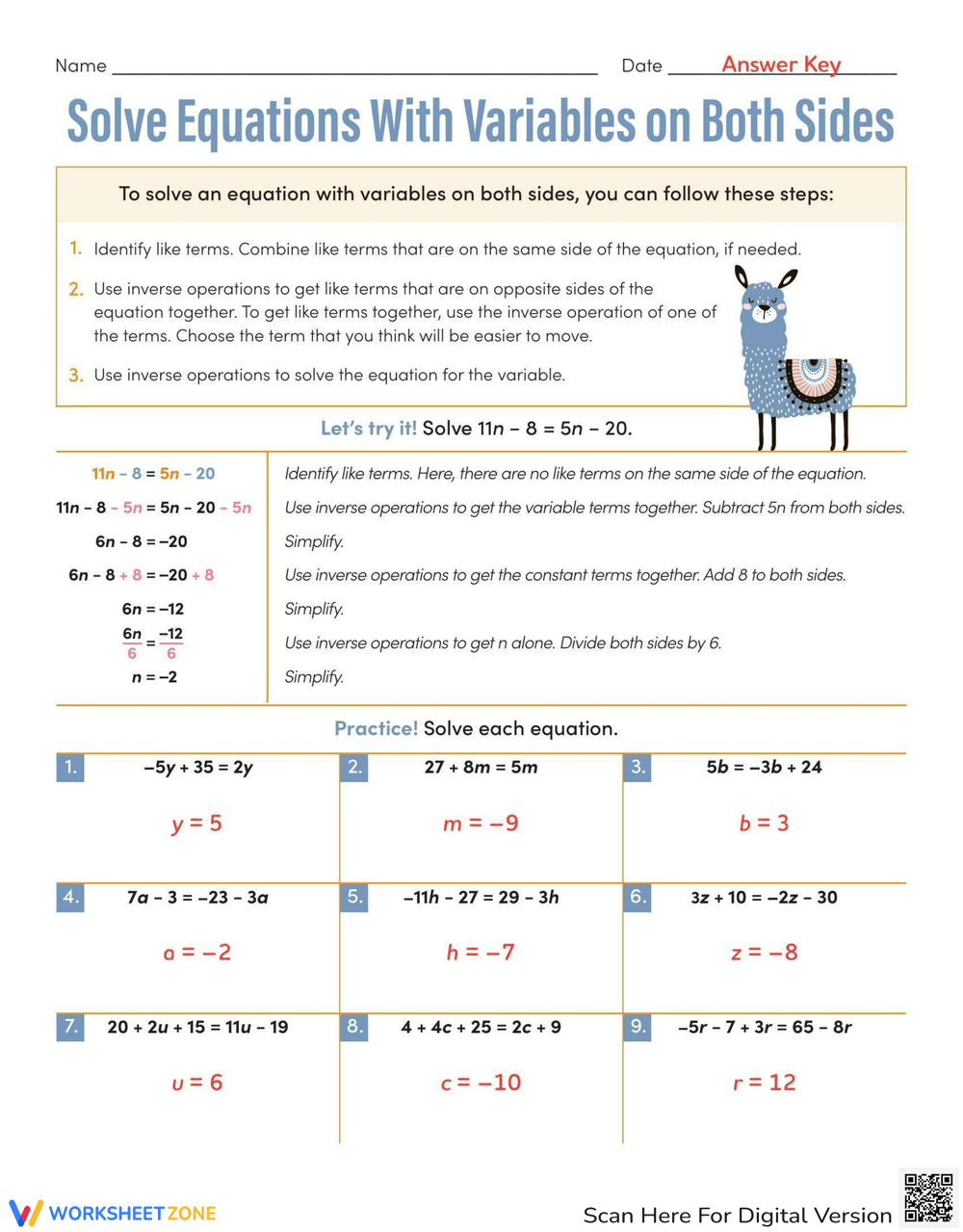
Solving Equations with X on Both Sides

To solve an equation with X on both sides, follow these steps:
- Combine like terms: Simplify both sides of the equation by combining any like terms.
- Add or subtract the same value to both sides: If there are constants on the same side as the variable, add or subtract the same value to both sides to isolate the variable.
- Multiply or divide both sides by the same value: If the variable is multiplied or divided by a constant, perform the inverse operation to both sides to isolate the variable.
- Simplify and solve: Simplify the equation and solve for the variable.
Example 1:

Solve for X: 2X + 5 = X + 11
📝 Note: This equation has X on both sides, and our goal is to isolate X.
Step 1: Combine like terms

- 2X + 5 = X + 11
- Move X to the left side: 2X - X = 11 - 5
- Simplify: X = 6
Example 2:

Solve for X: X - 3 = 2X + 2
📝 Note: This equation has X on both sides, and our goal is to isolate X.
Step 1: Combine like terms

- X - 3 = 2X + 2
- Add 3 to both sides: X = 2X + 5
- Subtract 2X from both sides: -X = 5
- Multiply both sides by -1: X = -5
Additional Tips and Tricks
- Check your work: Once you’ve solved the equation, plug the value back into the original equation to ensure it’s true.
- Use inverse operations: When solving equations, use inverse operations to isolate the variable. For example, if the variable is multiplied by a constant, divide both sides by that constant.
Practice Exercises
Practice makes perfect! Try solving the following equations with X on both sides:
- 3X + 2 = 2X + 7
- X - 4 = 3X - 1
- 2X = X + 9
| Equation | Solution |
|---|---|
| 3X + 2 = 2X + 7 | X = 5 |
| X - 4 = 3X - 1 | X = 3 |
| 2X = X + 9 | X = 9 |

Conclusion

Solving equations with X on both sides requires careful attention to detail and a solid understanding of algebraic properties. By following the steps outlined in this guide and practicing with sample equations, you’ll become proficient in solving these types of equations. Remember to check your work and use inverse operations to ensure accurate solutions.
What is the main goal when solving equations with X on both sides?
+
The main goal is to isolate the variable X by using algebraic properties and inverse operations.
How do I check my work when solving equations?

+
Plug the value of X back into the original equation to ensure it’s true.
What is the distributive property, and how is it used in solving equations?
+
The distributive property allows us to distribute a single term across the terms inside parentheses. It’s used to simplify equations and isolate variables.
Related Terms:
- equations on both sides pdf
- algebra unknown on both sides
- solving equations unknown both sides
- unknowns on both sides worksheet