Solving Equations With Variables on Both Sides Made Easy

Understanding the Concept of Solving Equations with Variables on Both Sides
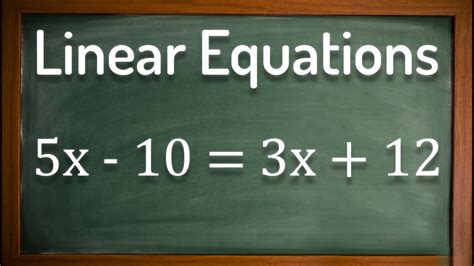
Solving equations with variables on both sides can be a challenging task for many students. However, with the right approach and understanding of the concept, it can become a straightforward process. An equation is a statement that says two things are equal, and it is denoted by the equal sign (=). When we have variables on both sides of the equation, our goal is to isolate the variable on one side of the equation.
Why Do We Need to Isolate the Variable?
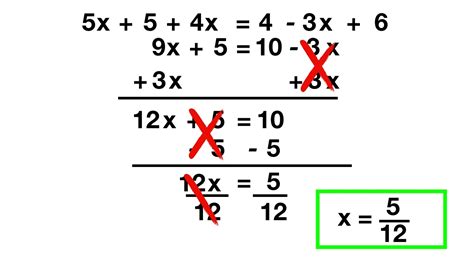
Isolating the variable is essential because it allows us to find the value of the variable. Think of it like solving a puzzle. When we have variables on both sides, it’s like having a puzzle with multiple unknowns. By isolating the variable, we can solve for its value, which is the key to solving the puzzle.
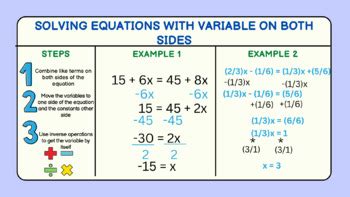
Step-by-Step Guide to Solving Equations with Variables on Both Sides
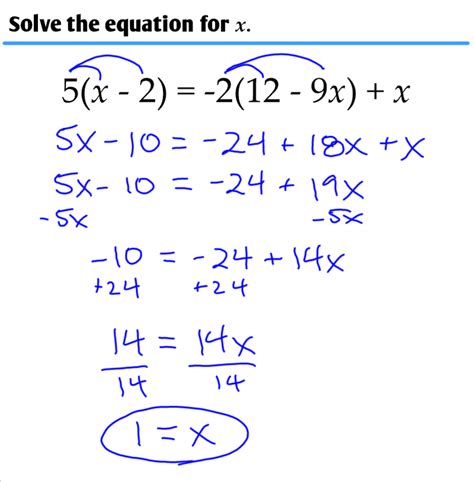
Here’s a step-by-step guide to solving equations with variables on both sides:
- Step 1: Write down the equation: Start by writing down the equation with variables on both sides.
- Step 2: Add or subtract the same value to both sides: To eliminate the variable on one side, add or subtract the same value to both sides of the equation. This will help you get closer to isolating the variable.
- Step 3: Multiply or divide both sides by the same value: If there are coefficients (numbers in front of the variable), multiply or divide both sides by the same value to eliminate them.
- Step 4: Simplify the equation: Simplify the equation by combining like terms.
Example 1: Solving a Simple Equation with Variables on Both Sides

Let’s solve the equation 2x + 3 = x + 5.
- Step 1: Write down the equation: 2x + 3 = x + 5
- Step 2: Subtract x from both sides: 2x - x + 3 = x - x + 5
- Step 3: Simplify the equation: x + 3 = 5
- Step 4: Subtract 3 from both sides: x + 3 - 3 = 5 - 3
- Step 5: Simplify the equation: x = 2
🤔 Note: When subtracting x from both sides, we are essentially eliminating the variable on the right side of the equation.
Example 2: Solving a More Complex Equation with Variables on Both Sides

Let’s solve the equation 4x - 2 = 2x + 10.
- Step 1: Write down the equation: 4x - 2 = 2x + 10
- Step 2: Add 2 to both sides: 4x - 2 + 2 = 2x + 10 + 2
- Step 3: Simplify the equation: 4x = 2x + 12
- Step 4: Subtract 2x from both sides: 4x - 2x = 2x - 2x + 12
- Step 5: Simplify the equation: 2x = 12
- Step 6: Divide both sides by 2: 2x / 2 = 12 / 2
- Step 7: Simplify the equation: x = 6
📝 Note: When adding or subtracting the same value to both sides, make sure to perform the operation on both sides of the equation.
Common Mistakes to Avoid

When solving equations with variables on both sides, it’s easy to make mistakes. Here are some common mistakes to avoid:
- Forgetting to perform the operation on both sides: Make sure to add, subtract, multiply, or divide both sides of the equation by the same value.
- Not simplifying the equation: Simplify the equation by combining like terms.
- Not checking your work: Double-check your work to ensure that you have isolated the variable correctly.
By following these steps and avoiding common mistakes, you can become a pro at solving equations with variables on both sides.
Solving equations with variables on both sides is a crucial skill in algebra and mathematics. With practice and patience, you can master this skill and become proficient in solving equations. Remember to always follow the steps, simplify the equation, and check your work to ensure that you have isolated the variable correctly.
What is the main goal when solving equations with variables on both sides?
+
The main goal is to isolate the variable on one side of the equation.
Why is it essential to simplify the equation?
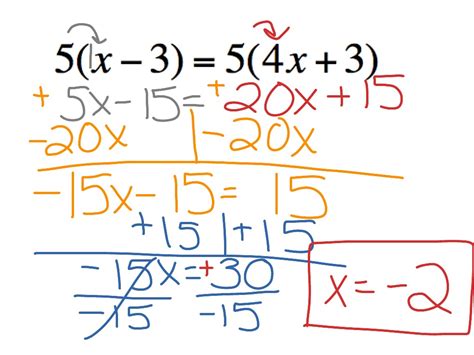
+
Simplifying the equation helps to eliminate unnecessary terms and makes it easier to isolate the variable.
What is the most common mistake when solving equations with variables on both sides?

+
Forgetting to perform the operation on both sides of the equation is the most common mistake.