7 Ways to Solve Equations with Fractions Easily

Introduction to Solving Equations with Fractions

Equations with fractions can be a daunting task for many students. However, with the right approach and techniques, solving these types of equations can become a breeze. In this article, we will explore seven ways to solve equations with fractions easily.
Method 1: Clear the Fractions by Multiplying Both Sides

One of the most effective ways to solve equations with fractions is to clear the fractions by multiplying both sides by the least common multiple (LCM) of the denominators. This will eliminate the fractions and allow you to solve the equation as you would with any other type of equation.
📝 Note: When multiplying both sides by the LCM, make sure to multiply every term in the equation, including the constants.
For example:
To solve this equation, we need to find the LCM of the denominators, which is 15.
Method 2: Use a Common Denominator
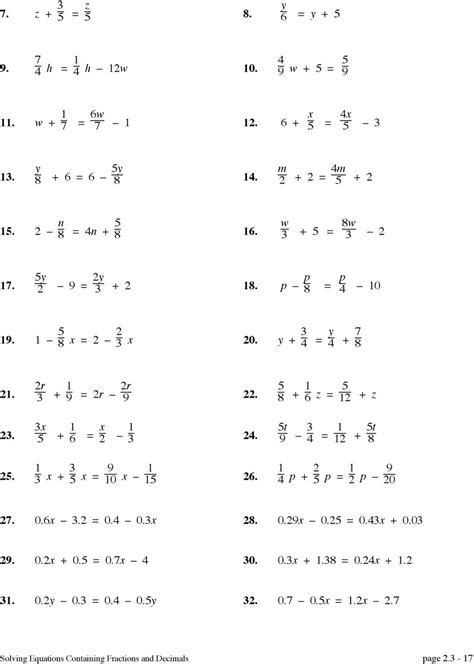
Another way to solve equations with fractions is to find a common denominator and rewrite the equation using that denominator.
For example:
To solve this equation, we can rewrite it using a common denominator of 12.
Method 3: Use Equivalent Fractions

Equivalent fractions are fractions that have the same value but different denominators. We can use equivalent fractions to solve equations with fractions by rewriting the equation using equivalent fractions.
For example:
To solve this equation, we can rewrite the fraction on the right side using an equivalent fraction with a denominator of 3.
Method 4: Use the Cross-Product Property

The cross-product property states that if we have two fractions that are equal, we can multiply the numerator of the first fraction by the denominator of the second fraction and set it equal to the product of the denominator of the first fraction and the numerator of the second fraction.
For example:
Using the cross-product property, we can rewrite the equation as:
Method 5: Solve the Equation by Inverting the Fractions
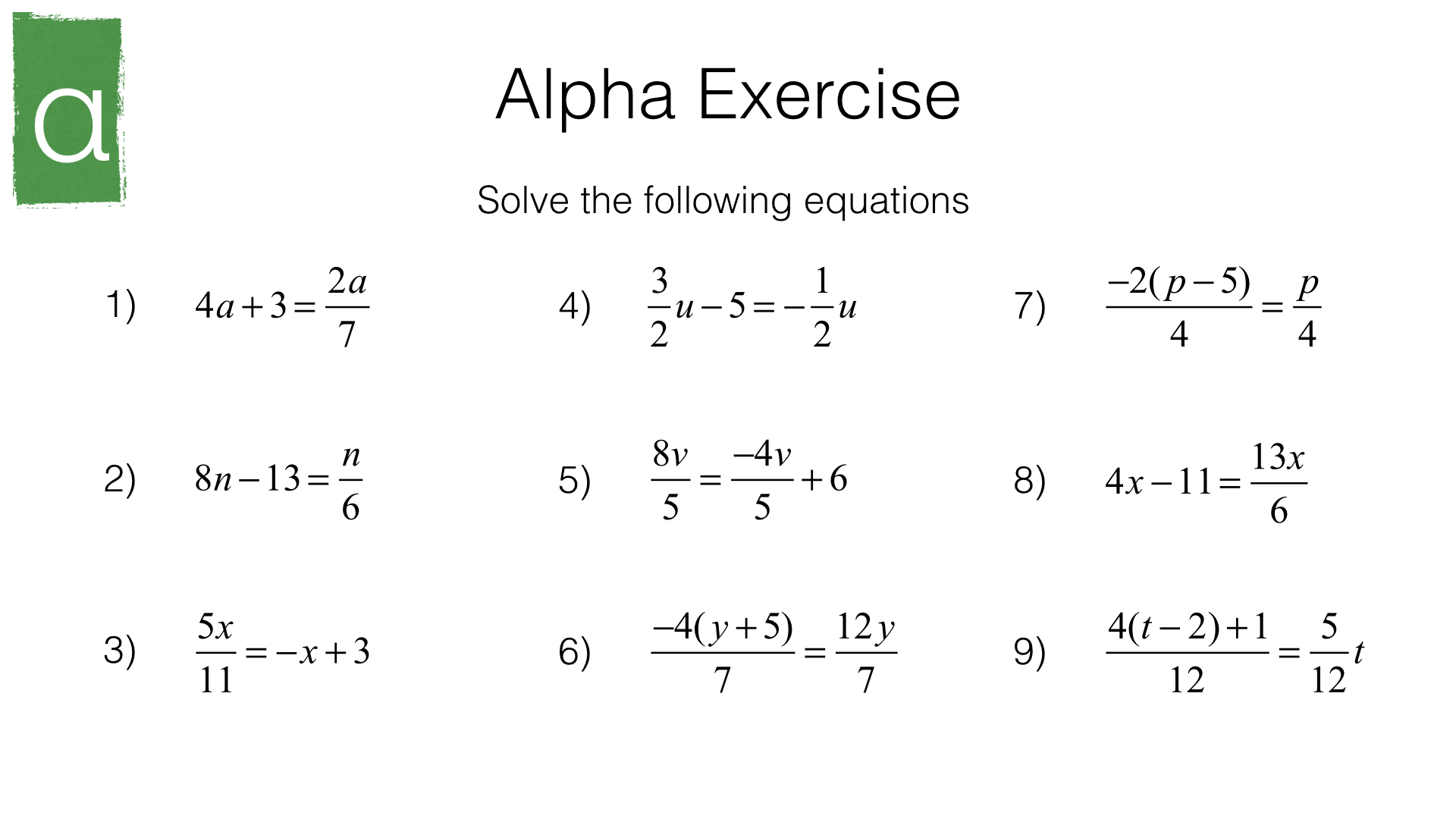
We can also solve equations with fractions by inverting the fractions. This means that we flip the numerator and denominator of each fraction and then solve the equation.
For example:
To solve this equation, we can invert the fractions and rewrite the equation as:
Method 6: Use a Formula to Solve the Equation

There are many formulas that we can use to solve equations with fractions. One of the most common formulas is the formula for solving linear equations with fractions:
Where a, b, c, and d are constants.
For example:
To solve this equation, we can use the formula:
Method 7: Use a Graph to Solve the Equation

Finally, we can use a graph to solve equations with fractions. This method involves graphing the two fractions on a coordinate plane and finding the point of intersection.
For example:
To solve this equation using a graph, we can plot the two fractions on a coordinate plane and find the point of intersection.
Using a graph to solve equations with fractions can be a powerful tool, especially when dealing with complex equations.
Now that we have explored seven ways to solve equations with fractions, let’s summarize the key points.
In conclusion, solving equations with fractions can be a challenging task, but with the right approach and techniques, it can become a breeze. By using one or more of the seven methods outlined in this article, you can easily solve equations with fractions and become more confident in your math skills.
What is the best way to solve equations with fractions?
+
The best way to solve equations with fractions is to use a combination of methods, such as clearing the fractions by multiplying both sides by the LCM, using a common denominator, and inverting the fractions.
How do I find the LCM of two fractions?

+
To find the LCM of two fractions, we need to find the least common multiple of the denominators. We can do this by listing the multiples of each denominator and finding the smallest multiple that they have in common.
What is the cross-product property?

+
The cross-product property states that if we have two fractions that are equal, we can multiply the numerator of the first fraction by the denominator of the second fraction and set it equal to the product of the denominator of the first fraction and the numerator of the second fraction.



