Master Solving Equations and Inequalities Worksheet Answers Here

Welcome to the ultimate guide to mastering solving equations and inequalities! Whether you're a high school student tackling algebra for the first time or brushing up on your skills before college-level courses, this guide will equip you with techniques, tips, and common mistakes to avoid. Let's dive into the world of mathematical equations and inequalities.

Understanding Basic Concepts

Before diving into the complexities of solving equations and inequalities, it’s crucial to understand some fundamental concepts:

• Equation: A mathematical statement where two expressions are equal.
• Inequality: A mathematical statement that includes a “not equal to” condition (>, <, ≥, ≤).

🔍 Note: Remember, when solving inequalities, you must flip the inequality sign when multiplying or dividing by a negative number.

Solving Linear Equations

Linear equations are the foundation of algebra. Here’s how to solve them:

1. Remove any fractions or decimals by multiplying by the lowest common denominator.
2. Isolate the variable on one side by using addition/subtraction to eliminate constants.
3. Use multiplication or division to isolate the variable from its coefficient.

Example of Solving a Linear Equation

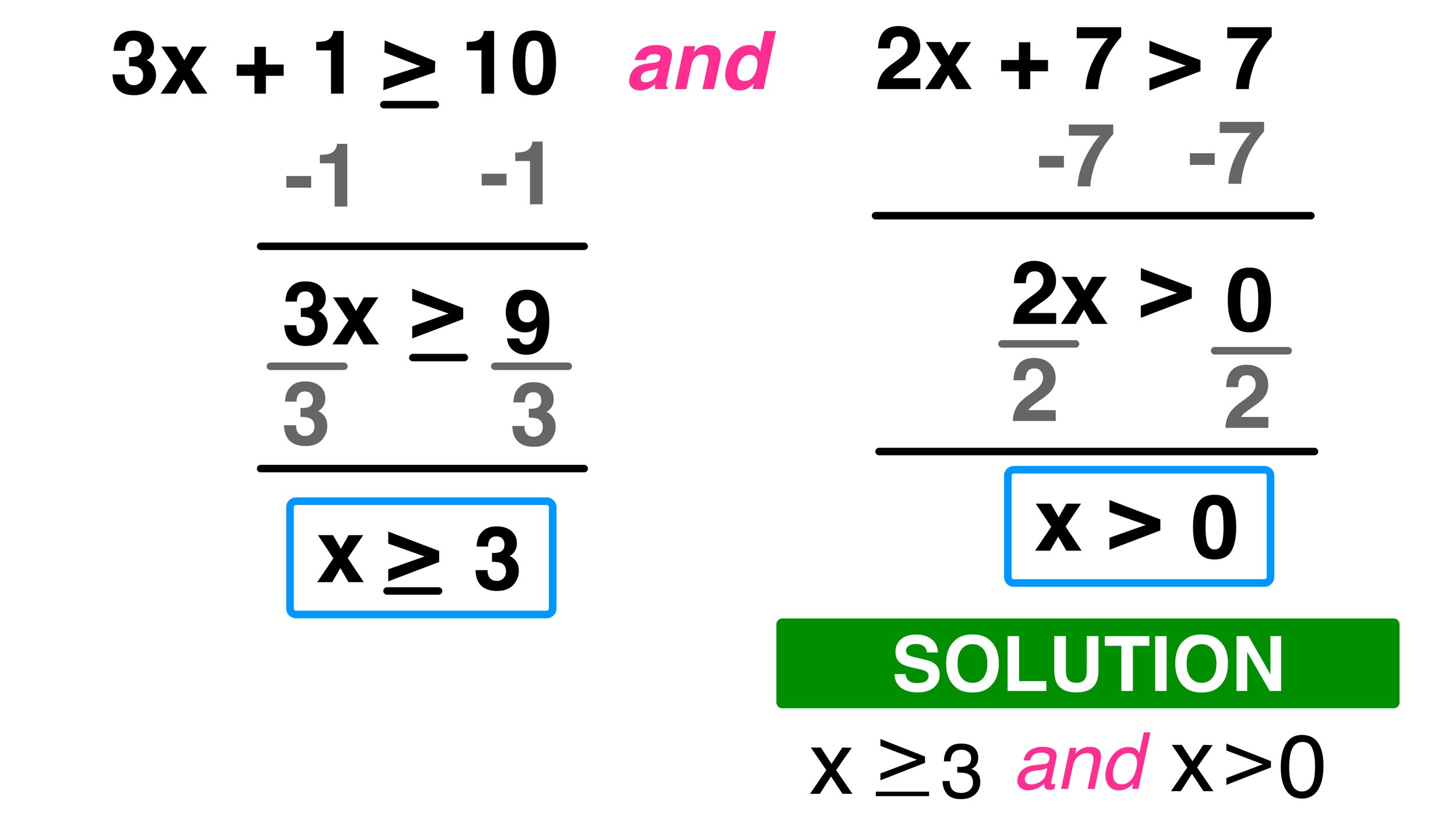
Let’s solve for ( x ) in ( 2x + 3 = 7 ):

1. Subtract 3 from both sides to isolate the term with x: ( 2x + 3 - 3 = 7 - 3 ), so ( 2x = 4 ).
2. Divide both sides by 2: ( x = \frac{4}{2} ), so ( x = 2 ).

Working with Inequalities

When solving inequalities, follow these steps:

• Maintain the order of operations (PEMDAS).
• Isolate the variable by performing the same operation on both sides.
• Remember to reverse the inequality sign if multiplying or dividing by a negative number.

Example of Solving an Inequality

Let’s solve ( 3x - 5 > 7 ):

1. Add 5 to both sides to move the constant to the right: ( 3x - 5 + 5 > 7 + 5 ), so ( 3x > 12 ).
2. Divide by 3, keeping the inequality sign as is: ( x > 4 ).

Quadratic Equations

Quadratic equations, represented by ( ax^2 + bx + c = 0 ), can be solved using various methods:

• Factoring: Break the quadratic into two binomials and set each to zero.
• Quadratic Formula: ( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} )
• Completing the Square: Adjust the equation to form a perfect square trinomial.

Example of Solving Quadratic Equation by Factoring

Solve for ( x ) in ( x^2 + 5x + 6 = 0 ):

1. Factor the quadratic: ( (x + 2)(x + 3) = 0 ).
2. Set each factor to zero: ( x + 2 = 0 ) or ( x + 3 = 0 ).
3. Solutions are ( x = -2 ) and ( x = -3 ).

Tips and Common Mistakes

Here are some tips and common errors to avoid:

• Always double-check your arithmetic.
• Watch out for distribution errors when multiplying or factoring.
• Remember that inequalities change when multiplying or dividing by negative numbers.
• Keep track of negative signs and understand their impact on operations.

💡 Note: Quadratic equations can sometimes have no real solutions; ensure you understand the discriminant when using the quadratic formula.

Summing Up Key Strategies

To become proficient in solving equations and inequalities:

• Understand the basic principles.
• Follow step-by-step methods for solving different types of equations and inequalities.
• Regularly practice with diverse problem sets to build fluency.
• Avoid common mistakes by being meticulous with arithmetic and sign changes.

By mastering these strategies, you’ll develop a deep understanding of algebra that will serve you well in further mathematical studies or in practical problem-solving.

What is the difference between an equation and an inequality?

+

An equation states that two expressions are equal, while an inequality uses symbols like >, <, ≥, ≤ to show that one expression is larger, smaller, or equal to another but not exactly the same.

How do you know when to flip the inequality sign?

+

The inequality sign must be flipped when you multiply or divide both sides of the inequality by a negative number. This rule reverses the relationship between the two sides.

Can a quadratic equation have no real solutions?

+

Yes, when the discriminant (( b^2 - 4ac )) is negative, there are no real solutions because the square root of a negative number is an imaginary number.