5 Proven Steps to Solve Compound Inequalities Easily

Dealing with compound inequalities can sometimes seem like a daunting task. Whether you are a student struggling to understand the concepts for an upcoming exam or a professional using mathematics in your daily work, solving these inequalities efficiently can greatly simplify problem-solving processes. This detailed guide will walk you through 5 proven steps to easily solve compound inequalities, ensuring you grasp both the theory and application.
Step 1: Understand the Basics of Inequalities

Before tackling compound inequalities, it’s crucial to have a solid foundation in basic inequalities:
- Linear Inequality: An inequality that involves only one variable and can be graphed as a straight line.
- Interval Notation: A way of representing sets of numbers with parentheses or brackets for inclusive or exclusive endpoints.
- Properties of Inequalities: Rules that govern how to manipulate inequalities, like adding, subtracting, multiplying, or dividing both sides by the same positive or negative number.
Image Here
Step 2: Identify the Compound Inequality

A compound inequality is formed by two or more simple inequalities connected by the word ‘and’ or ‘or’. Here are examples:
- Conjunction: -3 < x < 5
- Disjunction: x < -2 or x > 4
💡 Note: The conjunction requires both conditions to be true, while the disjunction means either condition can be true.
Step 3: Solve Each Inequality Separately

When solving compound inequalities, you handle each part individually:
- Isolate the variable in each inequality if it’s not already. Remember to treat and conditions together and or conditions separately.
- Perform operations on each part, ensuring to keep the inequality’s direction correct.
- Solve for the variable in both inequalities.
Here’s an example:
| Conjunction | Disjunction |
| -3 < x < 5 | x < -2 or x > 4 |
| Add 2 to all parts: | No change needed: |
| -1 < x + 2 < 7 | x < -2 or x > 4 |
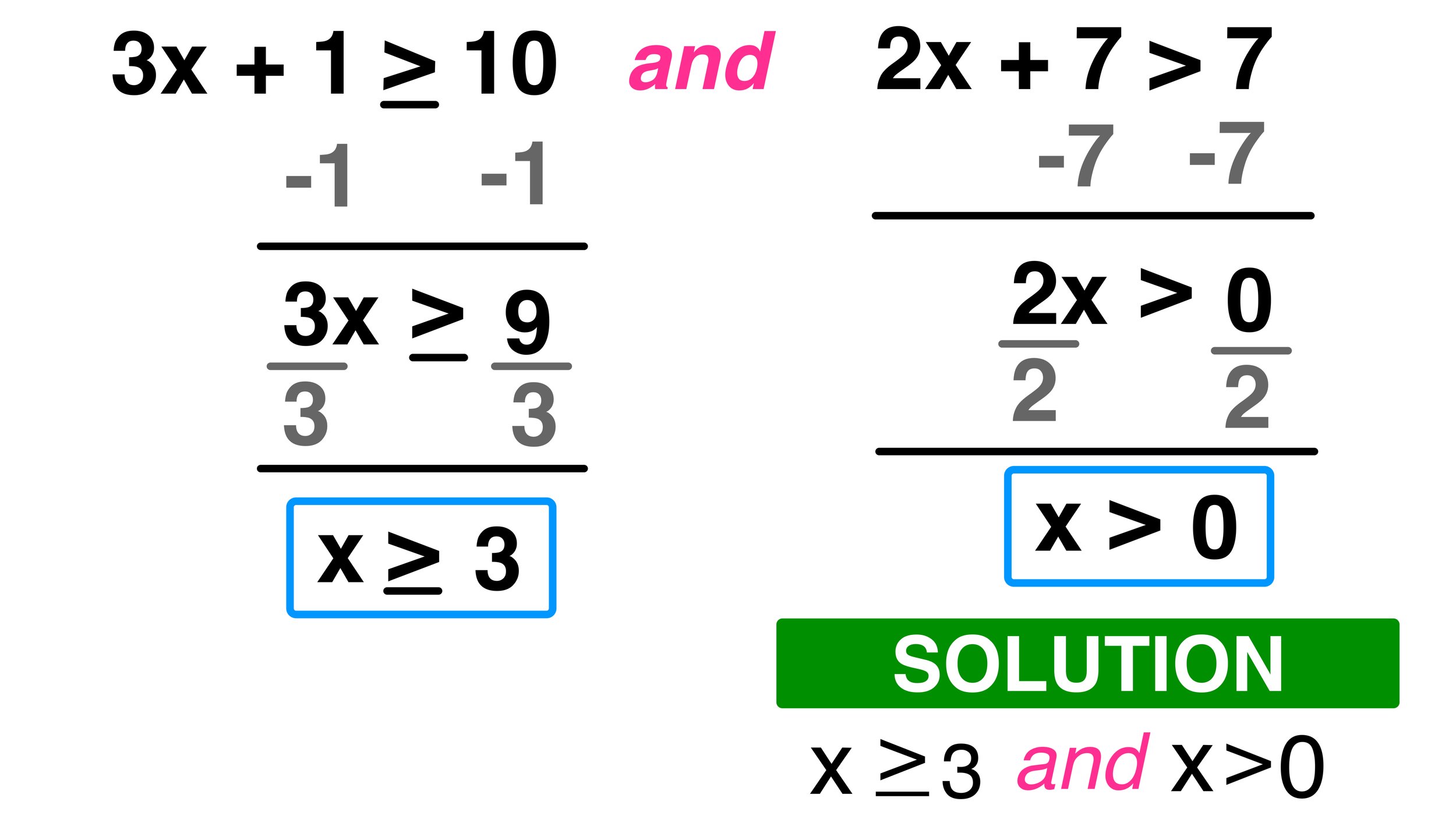
Step 4: Combine the Solutions

After solving each inequality, combine the solutions as follows:
- For and inequalities: The solution set includes only the numbers that satisfy both conditions. Represent this with a single interval or multiple intervals if needed.
- For or inequalities: The solution set includes any number that satisfies at least one condition. This might result in a union of disjoint intervals.
📚 Note: Use parentheses () for open intervals and brackets [] for closed intervals in your solution set notation.
Step 5: Graph and Interpret the Solution

Graphing the solution set provides a visual representation of the inequalities:
- Conjunction: Draw a continuous line or lines covering the interval where both conditions are true.
- Disjunction: Draw separate lines or sets of points for each part of the solution set.
Image Here
By following these five steps, you can systematically solve any compound inequality. Understanding the logic behind each step not only helps in solving the problem but also in interpreting the solutions in real-world contexts.
What is the difference between a conjunction and disjunction in compound inequalities?

+
A conjunction in inequalities means both conditions must be true simultaneously, usually represented with the word ‘and’. A disjunction, on the other hand, means that either one of the conditions can be true, represented with ‘or’.
How do I know if I should solve compound inequalities together or separately?

+
If the inequality contains ‘and’, solve the parts together; if it contains ‘or’, solve each part separately.
Why do we multiply or divide both sides of an inequality by the same positive or negative number?

+
Multiplying or dividing both sides by a positive number keeps the inequality sign the same. However, if you multiply or divide by a negative number, you must reverse the inequality sign to maintain the equivalence.