5 Easy Tips for Solving Inequalities Graphically

When it comes to algebra, inequalities can be as challenging as they are essential. Understanding how to solve them graphically not only enhances your grasp of mathematical concepts but also aids in visualizing solutions in a tangible way. In this post, we'll explore five easy tips that will help you master the art of solving inequalities using graphical methods.
Understanding Inequalities

Before diving into graphical solutions, it’s crucial to comprehend what inequalities are. An inequality compares two values or expressions, stating whether one is less than (<), greater than (>), less than or equal to (≤), or greater than or equal to (≥) the other. Here are the foundational points:
- Inequalities involve expressions that do not have an equal (=) sign.
- The solution to an inequality is a set of all possible values, making it different from equations which have exact solutions.
⚠️ Note: Inequalities differ from equations; they indicate a range rather than a single point.
Tip 1: Set Up the Coordinate Plane

The first step in solving inequalities graphically is setting up a coordinate plane. Here’s how you can proceed:
- Draw the x and y-axes, ensuring they are labeled clearly.
- If the inequality involves linear expressions, focus on the intercepts where the equation crosses the x or y-axis.

Tip 2: Graph the Boundary Line

Once your coordinate plane is ready, you’ll need to graph the boundary line:
- Replace the inequality symbol with an equals sign to find the equation of the boundary line. For example, for x + y > 3, the boundary line would be x + y = 3.
- Graph this line on your coordinate plane, considering whether the line should be solid (≤ or ≥) or dashed (< or >).
To graph linear inequalities:
- Find at least two points to plot the line. Common choices include the x-intercept and y-intercept.
- Connect these points with a straight line.
- Shade the region based on the inequality sign.
Tip 3: Shade the Correct Region
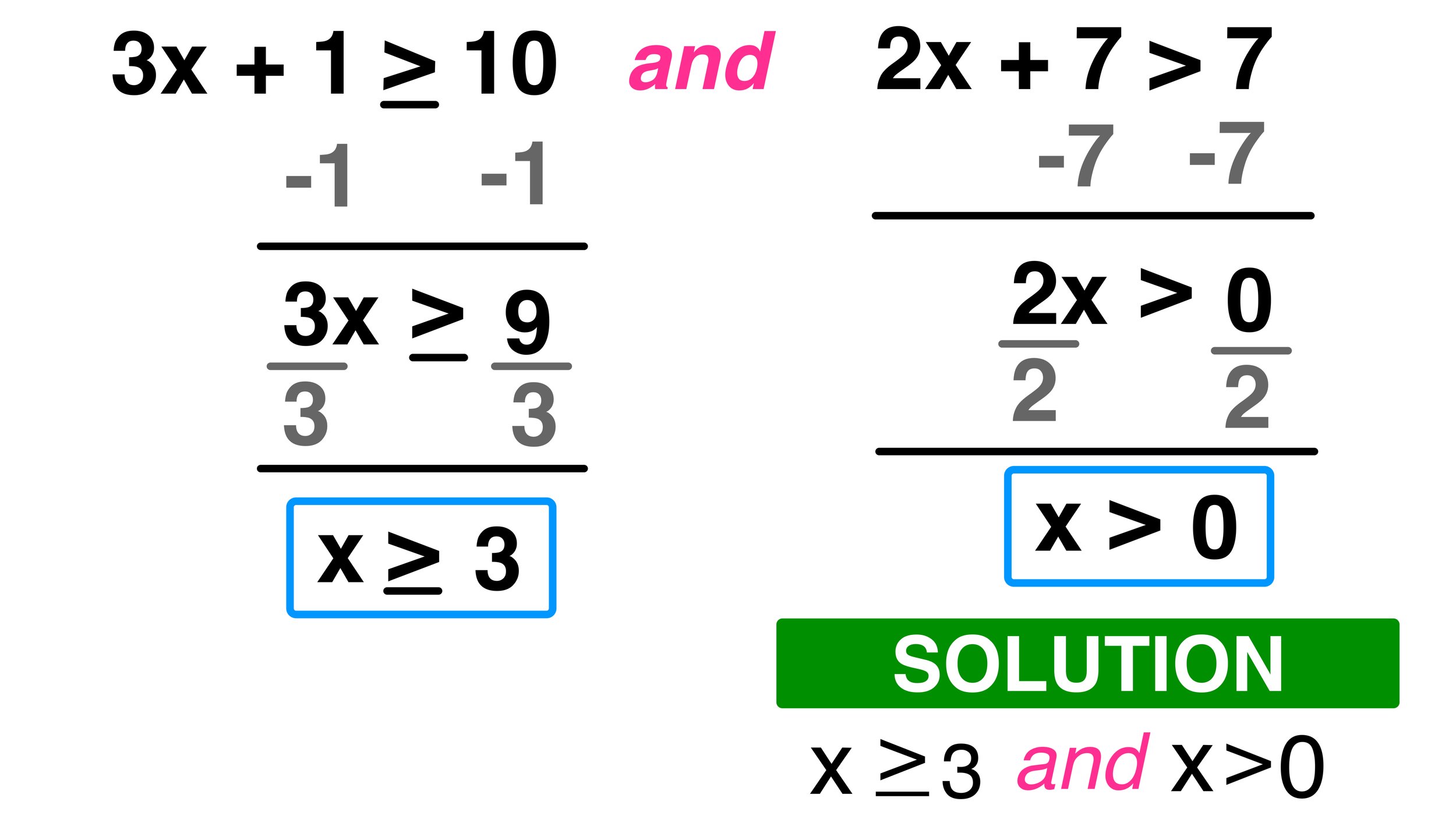
After graphing the boundary line, you need to shade the correct region:
- For inequalities with > or <, the boundary line is not part of the solution set, so you would use a dashed line and shade the appropriate side.
- For inequalities with ≥ or ≤, the boundary line is included, so use a solid line and shade accordingly.
- To determine which side to shade, pick a test point not on the line (usually (0,0) if it doesn’t lie on the line) and substitute it into the inequality. If it makes the inequality true, shade that side. Otherwise, shade the opposite side.
💡 Note: Using the point (0,0) as a test point simplifies the process if it's not on the boundary line.
Tip 4: Handle Multiple Inequalities

Sometimes, you’ll need to solve systems of inequalities. Here’s how:
| Step | Action |
|---|---|
| 1 | Graph each inequality as if it were a single one. |
| 2 | Determine the overlap of these regions. This area where all conditions are satisfied is your solution set. |
| 3 | If there’s no overlap, the system has no solution. |

Tip 5: Confirm the Solution

To ensure your graphical solution is correct:
- Test points within the shaded region. These points should all satisfy the original inequality.
- For linear inequalities, also consider checking boundary points, especially if you used a solid line.
📌 Note: If you're unsure about the boundaries or the correctness of shading, always test multiple points.
By mastering these five tips for solving inequalities graphically, you've gained a powerful tool for understanding and visualizing algebraic concepts. This approach not only deepens your grasp of the subject but also aids in problem-solving for various mathematical and real-world applications. Remember, the key to proficiency lies in consistent practice and understanding each step's significance in the process. Whether it's setting up the coordinate plane, graphing boundary lines, shading regions correctly, handling multiple inequalities, or confirming your solution, each tip builds on the last, creating a comprehensive strategy for tackling inequalities.
What is the difference between solving inequalities graphically and algebraically?

+
Solving inequalities graphically involves visualizing the solution set on a coordinate plane, which can provide an intuitive understanding of the range of solutions. Algebraic methods, on the other hand, involve manipulating the inequality through mathematical operations to isolate the variable, providing exact numerical bounds.
Can I use graphing to solve all types of inequalities?

+
Graphing can be effectively used for linear and some nonlinear inequalities. However, for complex inequalities like quadratic or higher order polynomials, graphing might not be the most efficient method due to the complexity of the shapes involved.
How do I choose which side to shade?

+
Choose a test point not on the line and substitute it into the inequality. If it satisfies the inequality, shade the side where the point lies. If not, shade the opposite side.