5 Tips for Solving Algebraic Equations Easily

1. Understand the Equation Structure

The first step in easily solving algebraic equations is to fully understand their structure. Algebraic equations typically involve variables, constants, and operations like addition, subtraction, multiplication, division, and sometimes exponents or square roots.
- Identify the variables: These are the unknowns, represented by letters like x, y, or z.
- Understand constants: These are numbers that do not change during the equation solving process.
- Recognize the operations: Knowing how these operations interact with each other and the variables is crucial.
💡 Note: Pay special attention to the signs (positive or negative) and how they affect the solution of the equation.

2. Simplify Expressions

Before attempting to solve for a variable, simplify both sides of the equation. This involves combining like terms, distributing constants over parentheses, and removing fractions by cross-multiplying or finding a common denominator.
- Combine like terms: Add or subtract terms that have the same variables and exponents.
- Use the distributive property: Expand expressions like 2(x + 3) to 2x + 6.
- Eliminate fractions: Multiply both sides of the equation by the common denominator to simplify operations.
| Original Expression | Simplified Expression |
|---|---|
| 2x + 3 + 5x - 4 | 7x - 1 |
| 3(2y + 1) - 2y | 6y + 3 - 2y = 4y + 3 |

✏️ Note: Ensure that each operation you perform maintains the equality of the equation.

3. Isolate the Variable

The goal of solving an equation is to isolate the variable on one side of the equation, usually the left, with all constants on the opposite side. Here are some techniques:
- Move terms to the other side: Add or subtract terms to both sides to cancel them out.
- Divide by coefficients: If the variable is multiplied by a number, divide both sides by that number.
- Handle exponents: Use square roots, cube roots, or logarithms to deal with exponents.
📚 Note: Performing the same operation on both sides of the equation ensures the balance is maintained.

4. Utilize the Quadratic Formula or Factorization

For quadratic equations, two powerful tools are factorization and the quadratic formula:
- Factoring: Break down the equation into two binomials whose product equals the original expression.
- Quadratic Formula: Use x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} where a, b, and c are coefficients from the standard form ax^2 + bx + c = 0.
🧠 Note: Factoring can be tricky; always ensure you have found all possible factors before concluding that an equation can't be factored.

5. Check Your Solution

Once you've found a solution, it's vital to check it to avoid errors. Here's how:
- Substitute the solution back into the original equation: Ensure both sides are equal.
- Reevaluate steps: Check if each step performed was valid and maintained the equation's equality.
🔍 Note: Checking your solution can often catch small calculation errors, which can drastically change the result.
To finalize, these five tips can significantly enhance your algebraic equation-solving skills, making complex problems approachable and solvable. Understanding the equation structure lays the groundwork for all other steps. Simplifying expressions reduces complexity, isolating the variable focuses your efforts, and using specific techniques like factorization or the quadratic formula can help conquer more intricate equations. Lastly, checking your solution ensures accuracy and can prevent simple mistakes from derailing your progress.
Why is understanding the equation structure important?

+
Understanding the equation’s structure provides insights into how to approach the problem, what operations are involved, and which strategies to use for simplification or solution.
Can simplifying an equation change its solution?
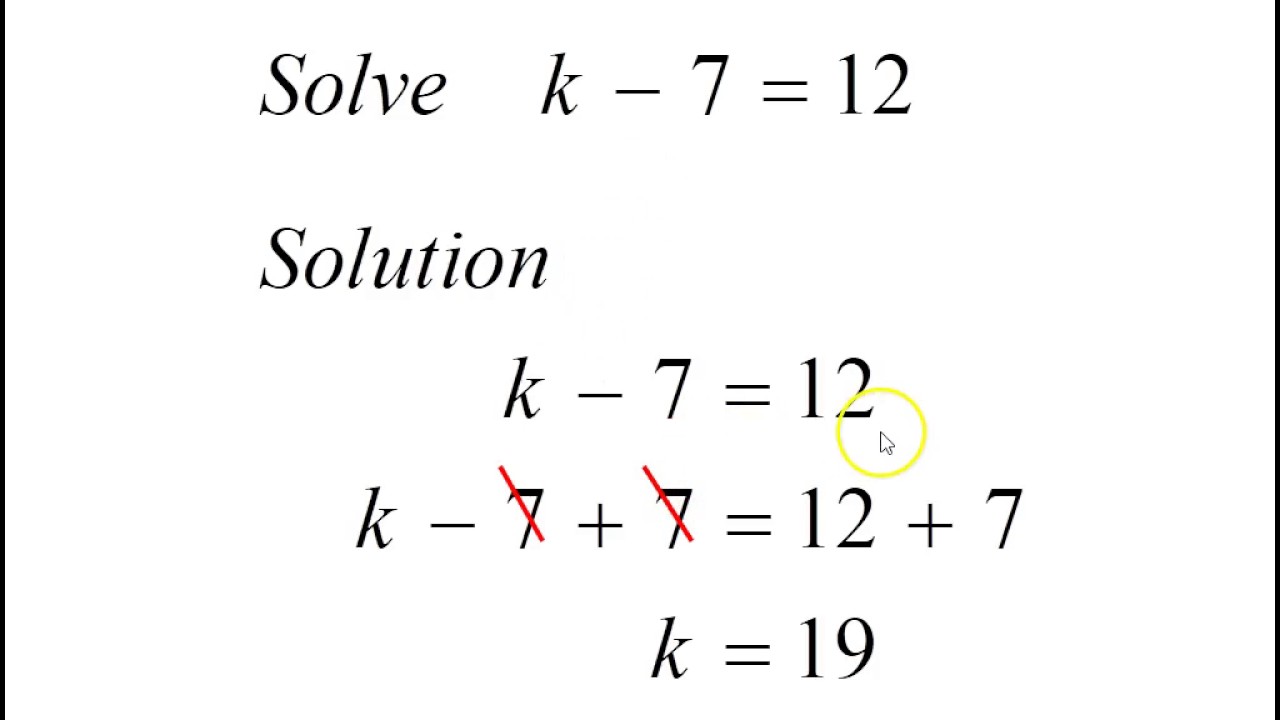
+
No, simplifying an equation does not alter its solution. It only rearranges the terms to make solving it easier. However, it’s important to perform operations that keep the equation balanced.
What if I can’t factorize the quadratic equation?

+
If factorization is not possible, you can use the quadratic formula, which provides solutions for all quadratic equations. This method is particularly useful when the roots are not easily identifiable by factorization.



