5 Easy Steps to Solve Systems of Equations

Learning how to solve systems of equations is a fundamental skill in algebra. Whether you are a student just starting out or someone looking to refresh their math skills, mastering this technique can significantly enhance your problem-solving abilities in various fields, from engineering to economics. Here, we'll explore five straightforward steps to crack systems of equations, making what often seems complex, quite approachable.
Step 1: Choose the Method

Before you dive into solving a system of equations, it’s crucial to select the right method. Here are the most common approaches:
- Substitution: Ideal when one of the equations can easily be solved for one variable.
- Elimination: Useful when you can eliminate one variable by adding or subtracting equations.
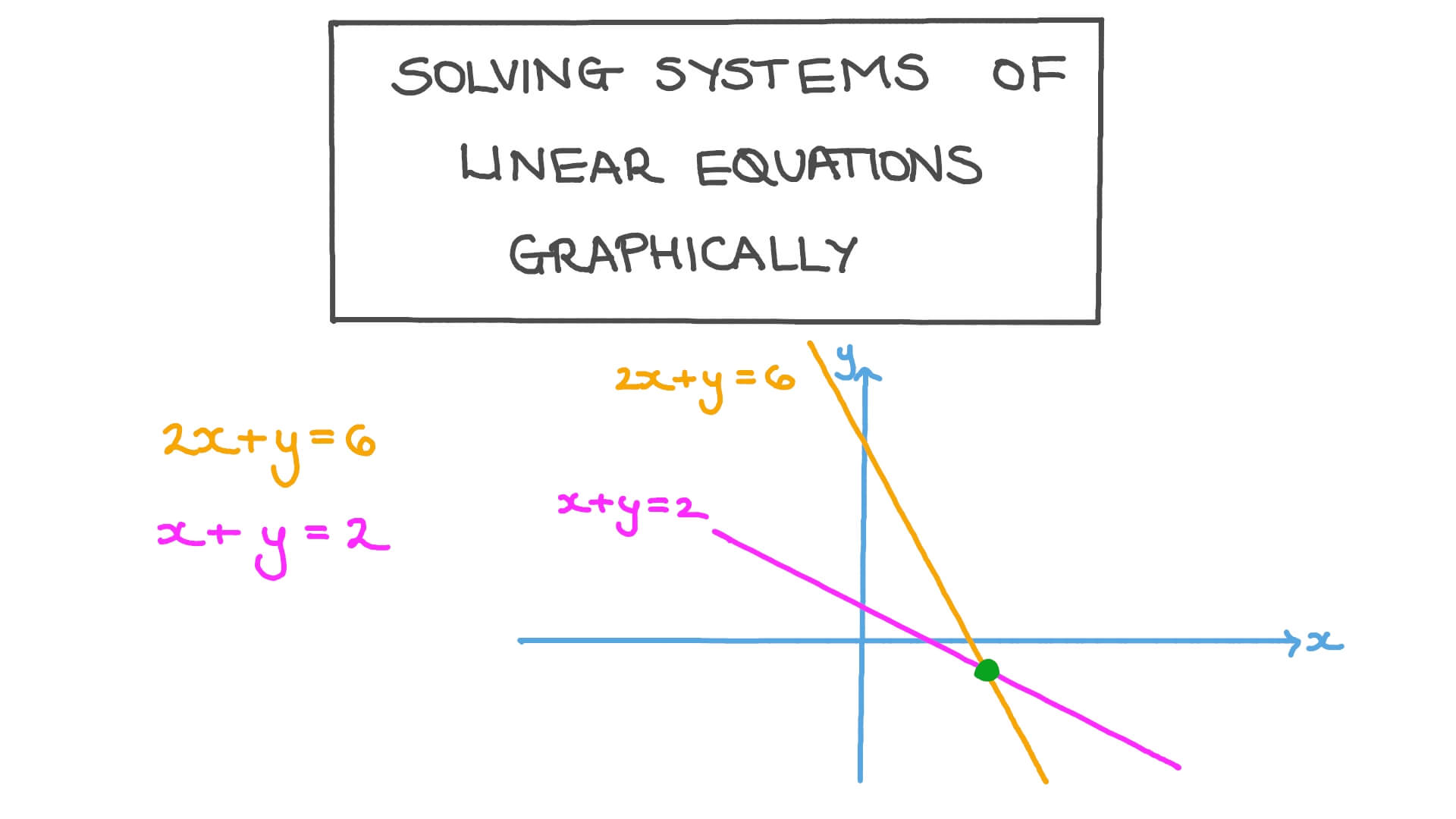
- Graphing: Visual method where you plot lines on a graph and find their intersection.
- Matrix: Involves using matrices and operations like row reduction or inverse matrices.
📊 Note: The method you choose can greatly affect the complexity and time taken to solve the problem.
Step 2: Arrange and Simplify

Once you’ve chosen your method:
- Write down your equations in a standard form, typically Ax + By = C, to simplify calculations.
- If you’re using elimination, make sure variables align for easy addition or subtraction.
- For substitution, isolate one variable in one of the equations.
- In matrix methods, organize your coefficients into a matrix to set up operations.

Step 3: Solve the Equations

Now, apply your chosen method:
- Substitution: Replace a variable from one equation into the other and solve for the remaining variable.
- Elimination: Make one variable coefficient the same in both equations (in magnitude but opposite in sign) and add or subtract to eliminate it.
- Graphing: Graph each equation and find the point of intersection.
- Matrix: Use row operations or matrix inversion to solve.
Step 4: Check Your Solution

After solving:
- Substitute your found values back into the original equations to ensure they hold true.
- Check each equation separately to confirm consistency in your solution.
🔍 Note: This step is critical as errors can easily creep in during calculations.
Step 5: Interpret Your Results
Once verified:
- Interpret what these solutions mean in the context of your problem or scenario.
- Are you looking for intersection points, slopes, or other mathematical interpretations?
- Consider if additional conditions need to be checked, like non-negative solutions in real-world applications.
In summary, solving systems of equations involves selecting the appropriate method, simplifying your setup, applying the method diligently, verifying your work, and finally interpreting your results. Each step is essential in ensuring accuracy and understanding, transforming what might initially appear daunting into a manageable task.
What are the most common types of systems of equations?

+
The most common types include linear systems (where lines intersect or are parallel) and non-linear systems (where one or more equations are not linear, leading to potentially multiple solutions or none at all).
Why is it important to check the solution in systems of equations?

+
Checking the solution ensures that the values you’ve calculated satisfy all original equations. This step helps catch any algebraic or arithmetic errors, which are common when manipulating equations.
When should I use substitution versus elimination?

+
Substitution is often quicker when one equation can easily solve for one variable. Elimination is preferable when the coefficients of one variable are similar or easily made so, allowing for simpler arithmetic operations.