5 Easy Steps to Solve One-Step Inequalities
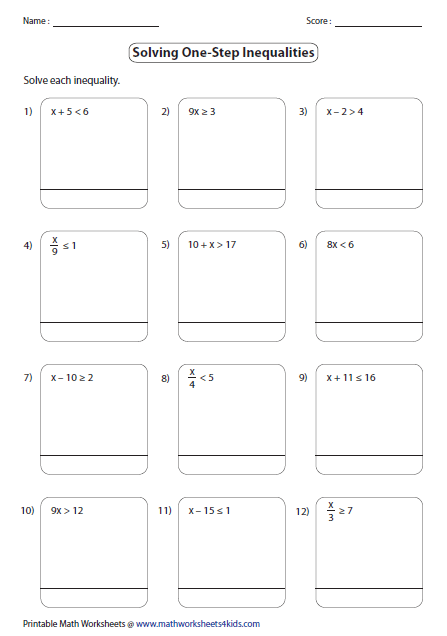
Understanding how to solve one-step inequalities is an essential algebraic skill that has numerous real-world applications, from budgeting to planning schedules. This blog post will walk you through the straightforward five-step process to solve these inequalities, offering insights, examples, and notes to enhance your learning experience.
Step 1: Translate the Problem
The first step in solving any inequality is to translate the verbal or written problem into a mathematical expression. Here’s how:
- Identify the variable: Usually, this will be a letter like x or y.
- Determine the inequality symbol: This could be >, <, ≥, or ≤.
- Translate any numerical information into mathematical terms, like “is less than,” “is at least,” or “is greater than.”
📝 Note: Pay close attention to words like “at least” or “no more than” which will dictate the type of inequality symbol you use.
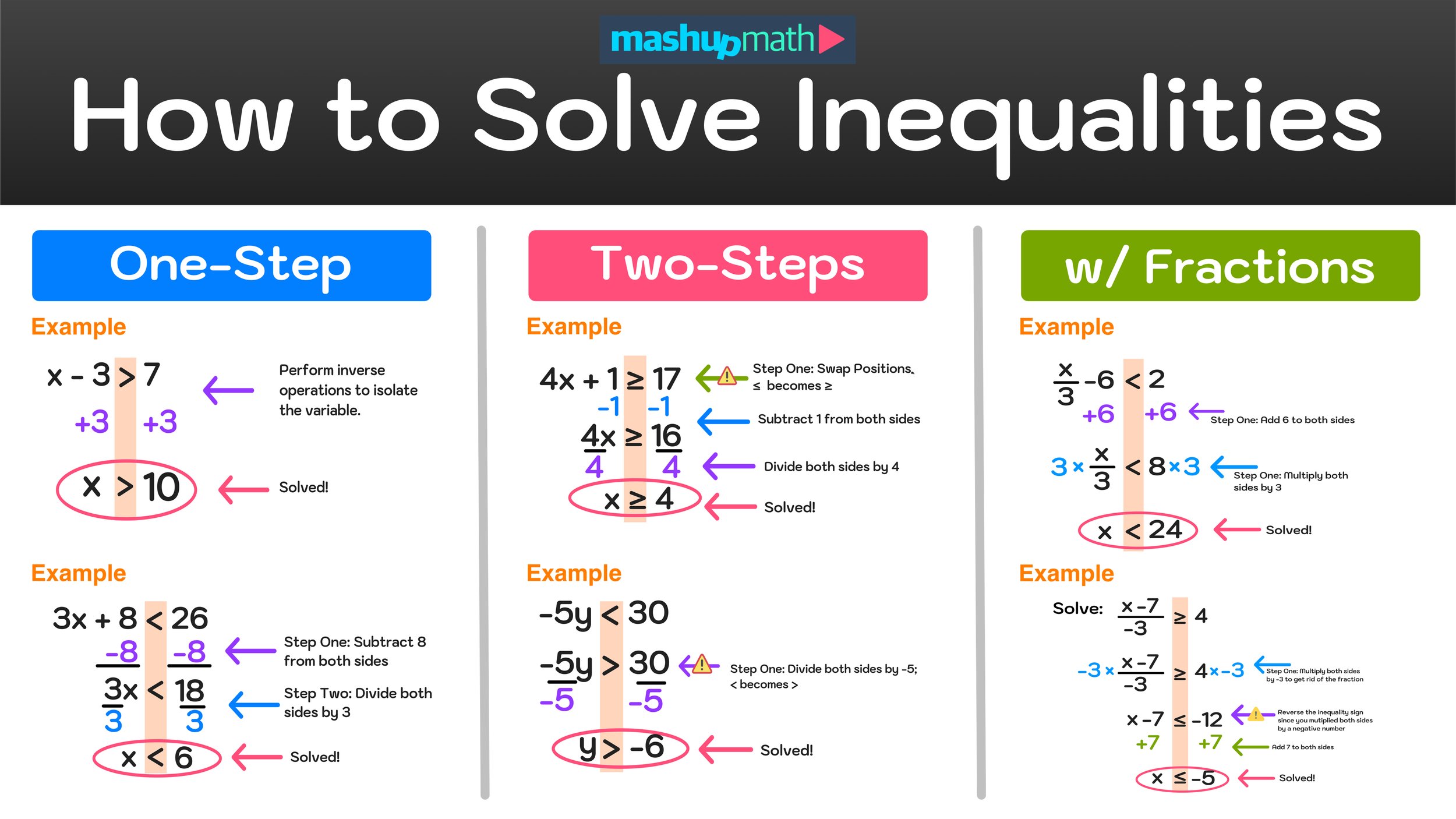
Step 2: Isolate the Variable

To isolate the variable, you’ll need to undo the operation that’s currently affecting the variable. Here are the steps:
- If the variable is being added, subtract that value from both sides.
- If the variable is being subtracted, add that value to both sides.
- If the variable is multiplied by a number, divide both sides by that number.
- If the variable is divided by a number, multiply both sides by that number.
This keeps the inequality balanced. Remember to reverse the inequality symbol if you multiply or divide by a negative number.
📝 Note: Reversing the inequality symbol is crucial when dealing with negative numbers to keep the inequality balanced.
Step 3: Solve the Inequality

Now that the variable is isolated, solve for its value:
- If the variable is on the left side, you can find the solution set.
- If the variable is on the right side, you might need to switch sides to match the variable to the left side for simplicity.
Let’s look at an example:
If you have 2x < 10, divide both sides by 2:
2x/2 < 10⁄2
x < 5
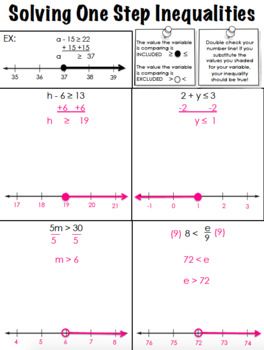
Step 4: Graph the Solution Set

Graphing helps visualize the solution. Here’s what to do:
- Draw a number line.
- If the inequality includes the equal part (≥, ≤), use a closed circle to represent that the value could be included.
- If the inequality does not include the equal part (>, <), use an open circle to show that the value is not included.
- Shade the line in the direction of the inequality.
Step 5: Check Your Solution

Lastly, plug a value from your solution set back into the original inequality to ensure it works:
- Choose a number from your solution set.
- Substitute it into the original inequality.
- If it satisfies the inequality, your solution is correct.
📝 Note: Don’t forget to check if the endpoint or boundary values are inclusive or not by looking at the original inequality sign.
In conclusion, solving one-step inequalities involves translating the problem, isolating the variable, solving it, graphing the solution, and verifying the result. Each step builds upon the last, making this a manageable task once you understand the process. With these steps, you can tackle more complex inequalities, apply your knowledge to real-life scenarios, and gain confidence in your algebraic abilities.
What does reversing the inequality symbol mean?

+
Reversing the inequality symbol involves changing > to < or vice versa when multiplying or dividing both sides of an inequality by a negative number to maintain the inequality’s truth.
Can you solve an inequality if it includes division or multiplication?

+
Absolutely! When the variable is multiplied or divided by a number, perform the inverse operation to isolate it. Remember to adjust the inequality symbol if the number is negative.
How do you graph inequalities?

+
To graph inequalities, draw a number line, place an open or closed circle at the boundary value, and shade the line in the direction of the inequality.
What are some real-life applications of solving inequalities?

+
Inequalities are used in financial planning, setting up budgets, determining production schedules, or even in game theory to find optimal strategies.
Why do we check our solution in inequalities?
+
Checking the solution helps confirm that the inequality is still true when a solution from the set is substituted back into the original inequality, ensuring no mistakes were made in the solving process.