Graphing Systems: Solve Equations Easily Worksheet Guide

Are you struggling with graphing systems of linear equations? Don't worry, you're not alone. Mastering this fundamental skill in algebra can open up a world of problem-solving capabilities, making complex problems more manageable. This guide will walk you through the steps to solve linear systems through graphing, offering a straightforward approach to understanding and mastering this essential math technique.
Why Graph Systems of Equations?
Graphing systems of equations visually represents the solutions, making it easier to:
- Understand where two lines intersect, if at all.
- Identify if the system has no solution, an infinite number of solutions, or exactly one solution.
- Visualize the relationships between different equations.
Getting Started: The Basics of Graphing

What You Need:

- A pencil, paper, and perhaps a ruler for precision.
- A basic understanding of linear equations.
- Graph paper, or a graphing calculator for digital precision.
Before diving in, let's remember that each equation in a system will be represented by a line on your graph. Here's how you proceed:
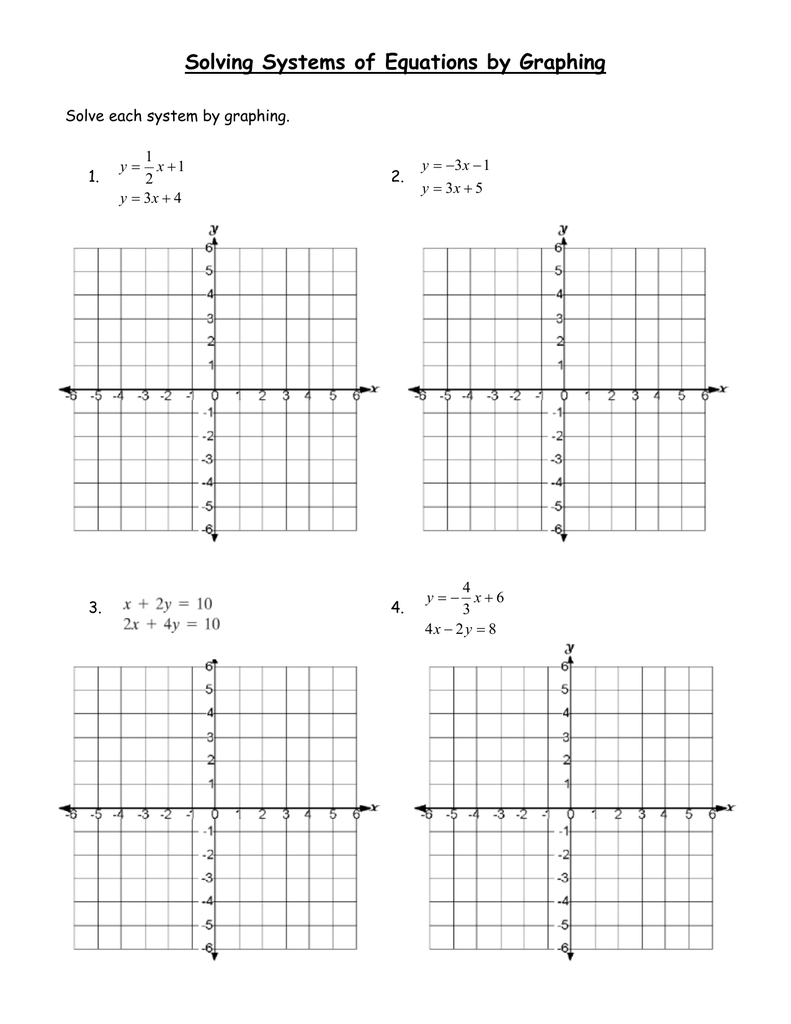
Step 1: Identify the Equations

First, ensure you have all the equations listed. For example:
- Equation 1: 2x + 3y = 6
- Equation 2: x - y = 1
Step 2: Convert to Slope-Intercept Form
Graphing is easier if you express each equation in slope-intercept form, which is y = mx + b:
- Equation 1: 2x + 3y = 6
- Solve for y: 3y = -2x + 6
- y = -\frac{2}{3}x + 2
- Equation 2: x - y = 1
- Solve for y: y = x - 1
Step 3: Plot the Lines
Using graph paper:
- Plot two points for each equation or use the slope and y-intercept to draw the lines.
- For the first equation, y = -\frac{2}{3}x + 2, plot y-intercept at (0, 2) and use slope to find another point, say (3, 0).
- For the second equation, y = x - 1, plot y-intercept at (0, -1) and another point using the slope, say (1, 0).
Step 4: Find the Intersection

The point where the lines cross is the solution to the system:
| Equation | Line |
|---|---|
| 2x + 3y = 6 | y = -\frac{2}{3}x + 2 |
| x - y = 1 | y = x - 1 |
📝 Note: Accuracy is key. Ensure your lines are straight, and check your work by substituting the solution back into the original equations.
Advanced Techniques
Using Technology
Graphing calculators or software can quickly plot lines:
- Enter the equations, and the device will plot them.
- Use the 'trace' or 'intersection' feature to find where the lines meet.
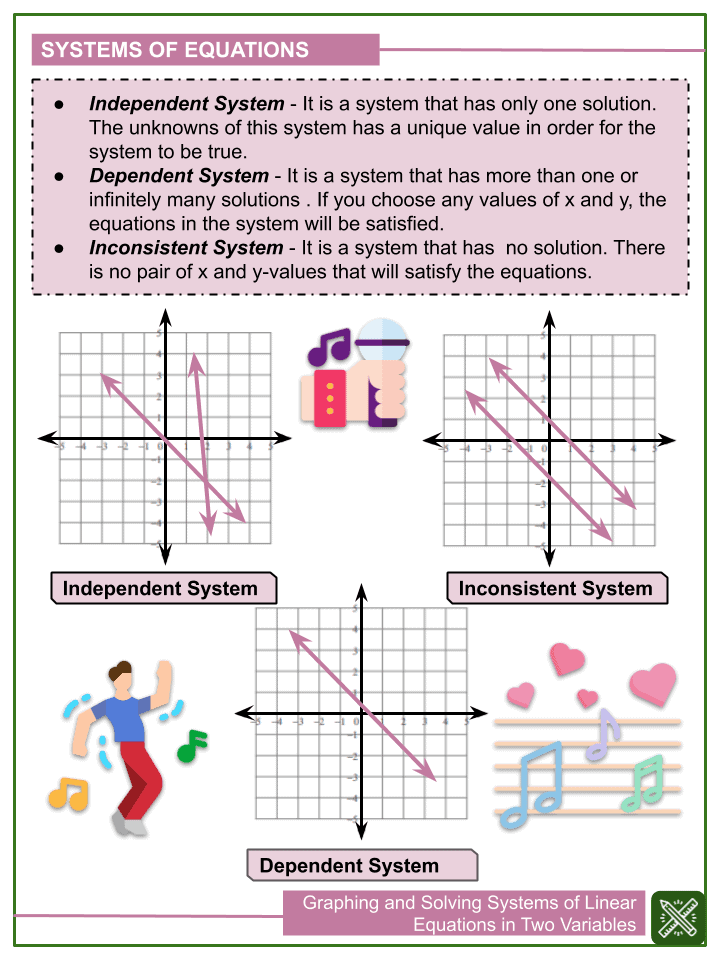
Recognizing Special Cases

- No Solution: When the lines are parallel and do not intersect.
- Infinite Solutions: When the lines overlap completely.
- One Solution: When lines intersect at exactly one point.
Recognizing these scenarios saves time and guides your problem-solving strategy.
Tips for Success

- Verify your solutions by substituting back into original equations.
- Use different colors for different lines to visually distinguish them.
- Keep your lines as accurate as possible. Small errors can lead to incorrect solutions.
📚 Note: Regular practice enhances both speed and accuracy in solving systems by graphing.
By following these steps, graphing systems of linear equations becomes not just a manageable task, but an enjoyable one. It's a tool that allows you to visualize mathematical relationships, identify solutions, and understand the interaction between different linear equations. As you continue to practice, you'll find that graphing not only helps in solving problems quickly but also in understanding the underlying principles of algebra better. Remember, mastering this method paves the way for more complex problem-solving in mathematics and beyond.
Why is graphing systems of equations useful?
+
Graphing systems of equations provides a visual method to find solutions, understand relationships, and identify special cases such as parallel or coinciding lines.
How do I know if my graphing work is accurate?

+
Substitute your graphical solution back into the original equations to verify if they satisfy both. If not, double-check your slope calculations and plotting accuracy.
What should I do if the lines don’t seem to intersect?
+
Extend your graph lines further or use technology to zoom in or use an intersection feature. Alternatively, check if the lines are parallel or if there might be an error in your equations or calculations.
Can technology always find the intersection?
+Yes, most graphing calculators and software have features to locate the intersection precisely. However, ensure the intersection is within the visible graph or use functions to find it.
What are some common mistakes in graphing?
+Common errors include miscalculating the slope or y-intercept, not extending lines far enough to see intersections, or drawing lines too hastily, leading to inaccuracies.