Inequality Solver: Graphing Made Easy Guide

Discovering the essence of algebraic inequalities not only empowers you to solve mathematical equations but also allows for better decision-making, optimization problems, and even financial strategies. In this comprehensive guide, we'll unravel the intricacies of solving inequalities using visual tools like graphs, which can significantly simplify the process and deepen understanding.
Understanding Inequalities

An inequality is not a mere balance of equal numbers; it’s a statement about the relative size or order of two mathematical expressions. Instead of the equals sign (=), we use symbols like <, >, ≤, or ≥.
Here are the basic types of inequalities:
- Less than () : x < 5
- Greater than () : x > 3
- Less than or equal to () : x ≤ 2
- Greater than or equal to () : x ≥ -1
💡 Note: Always remember that inequalities, unlike equations, do not preserve the equality of numbers but their order.
Why Use Graphs to Solve Inequalities?

The graph of an inequality can give you immediate visual feedback on where solutions lie, making complex problems more intuitive:
- Visual Aid: Seeing where numbers fall on a number line or within a coordinate system helps conceptualize the solution set.
- Multiple Solutions: Graphs can depict the range of all possible solutions at a glance.
- Interactivity: Modern graphing tools offer interactive methods to explore solutions, providing instant feedback.
Graphing Linear Inequalities

One Variable Inequality

For inequalities involving one variable, you can plot the solution set on a number line:
- Isolate the variable on one side.
- Determine the boundary points.
- Graph the boundary points with a solid circle for ≤ or ≥ and an open circle for < or >.
- Shade the part of the number line where the solution set lies.
Consider solving 3x + 5 > 17:
- Subtract 5 from both sides: 3x > 12.
- Divide by 3: x > 4.
- Graph the solution with an open circle at 4 and shade to the right of it.
Two Variable Inequality

When dealing with two variables, the graph turns into a plane. Here’s how to proceed:
- Transform the inequality into standard form: Ax + By < C or Ax + By > C.
- Sketch the line defined by the equality (Ax + By = C), considering whether it's a solid or dotted line.
- Choose a test point outside the line (for instance, (0,0)) to determine which side to shade.
- Shade the appropriate region.
Example: Graph x + 2y ≥ 4
- The equation x + 2y = 4 gives us a boundary line.
- Plot the line, making it solid since we use ≥.
- Test the point (0,0). If it doesn't satisfy the inequality, shade the opposite side of the line.
| Test Point | Is it in the solution set? |
|---|---|
| (0,0) | 0 + 2(0) ≥ 4, No, it's not |

Systems of Inequalities

Systems of inequalities involve solving multiple inequalities simultaneously. The solution is the intersection of all individual solutions:
- Graph each inequality on the same coordinate plane.
- The overlap region represents the solution to the entire system.
Example: Solving the system
- x + y > 2
- 2x - y > 0
- y ≤ 3
Graph each inequality:
- x + y = 2 (solid line, shade above)
- 2x - y = 0 (dotted line, shade above)
- y = 3 (solid line, shade below)
🗣️ Note: For systems, the more inequalities you have, the smaller the overlap (solution) will likely be.
Advanced Inequality Solving

Some inequalities require special techniques:
Absolute Value Inequalities

When dealing with absolute values, remember:
- |x| < a is equivalent to -a < x < a
- |x| > a is equivalent to x < -a or x > a
Solving |x + 1| < 3:
- Convert to a compound inequality: -3 < x + 1 < 3.
- Adjust to isolate x: -3 - 1 < x < 3 - 1, or -4 < x < 2.
- Graph this as two open circles on -4 and 2, shading the part between them.
Quadratic and Polynomial Inequalities

These inequalities can be solved by:
- Setting the polynomial to zero to find critical points.
- Graphing the polynomial as a curve.
- Shading regions based on the inequality's direction.
⚠️ Note: Polynomial inequalities can have multiple critical points, leading to a potentially complex solution set.
Strategies and Tricks for Graphing Inequalities

- Sign Analysis: Use number lines to analyze the sign changes of functions, especially helpful for polynomial and rational inequalities.
- Symmetry and Roots: Look for symmetry and roots to aid in graphing.
- Test Points: Use test points strategically to quickly narrow down the solution region.
Graphing inequalities might seem daunting, but with practice and the right tools, you'll master this essential skill. Inequality graphs provide not just solutions but a whole landscape of possibilities, allowing for quick analysis of various scenarios. By understanding and practicing these techniques, you'll find that inequalities can become intuitive and even fun to solve.
As we've explored, the visual representation of inequalities through graphs can make a complex problem simpler and more accessible. The tools and methods we've discussed provide a framework for approaching inequality-solving with confidence. With this knowledge, you're well-equipped to tackle any inequality problem that comes your way, and perhaps discover new ways to optimize, analyze, or navigate through life's many variables.
Why do we shade the solution region on a graph?
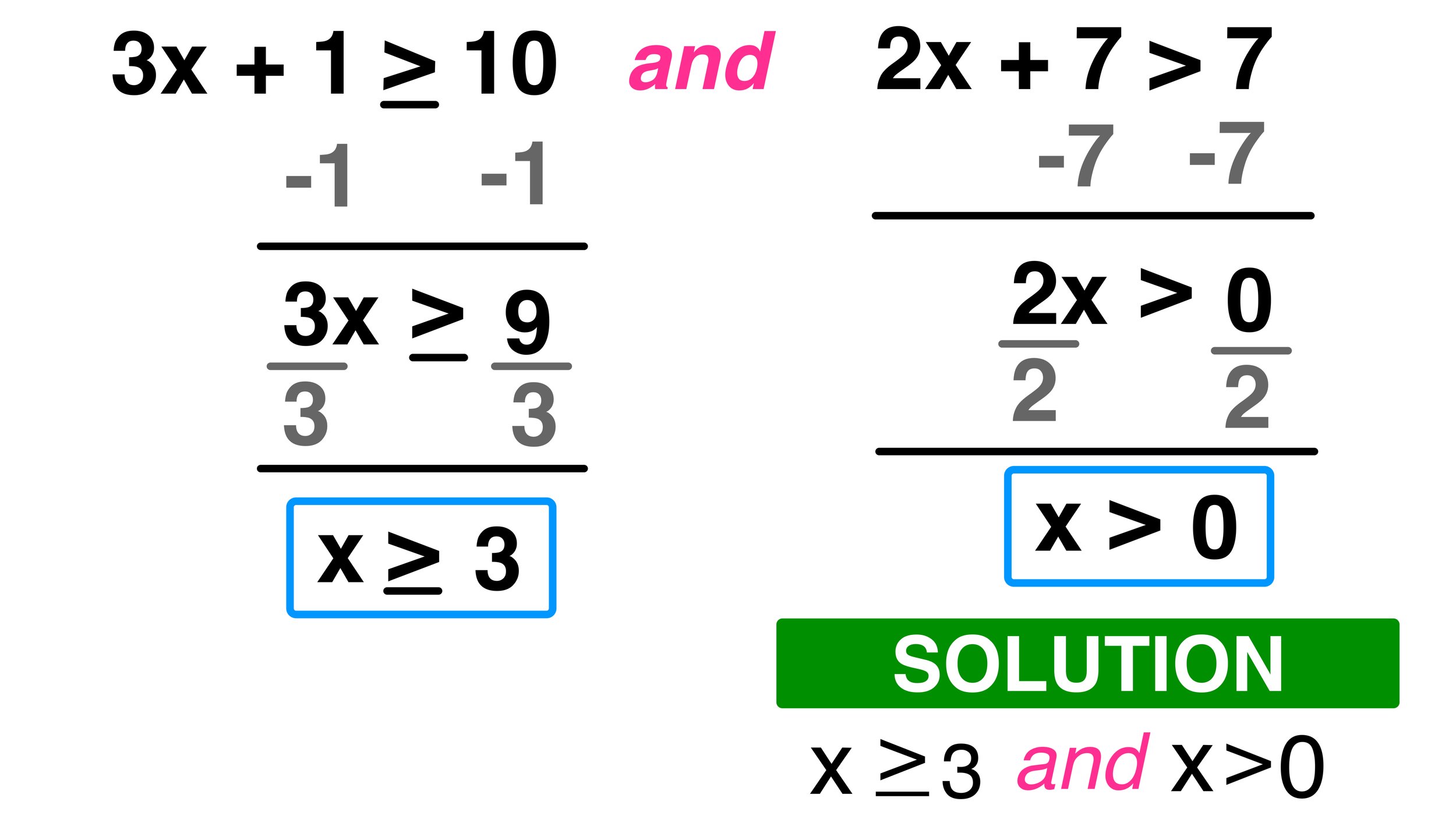
+
Shading helps visually identify where the inequality holds true. This visual cue aids in quickly determining the solution set by showing all numbers or points that satisfy the inequality.
How can you tell if an inequality is strict or inclusive?

+
If the inequality includes ≤ or ≥, it’s inclusive, meaning the boundary points are part of the solution set, and you’ll graph these with solid lines or circles. If it’s < or >, it’s strict, and you’ll use dotted lines or open circles to indicate the boundary points are not included.
What are some real-world applications of solving inequalities?

+
In real-world scenarios, inequalities can help with budget planning, optimization in logistics, decision-making in business strategies, scheduling, and designing engineering systems, among many other applications.



