Slope Review Worksheet: Quick Answer Guide

Geometry and algebra often intersect in fascinating ways, with slope being one of the key concepts bridging the two. Slope is essentially the measure of how steep a line is, and understanding its properties is fundamental for students and professionals alike. This comprehensive guide will delve into the nuances of slope, providing you with a quick review, examples, and practical tips to ensure you grasp this critical mathematical concept.
Understanding Slope

Slope is the rate of change between two points on a line. It tells you how much the y-value changes for each unit increase in the x-value. Mathematically, it is expressed as:
Slope (( m )) = (\frac{y_2 - y_1}{x_2 - x_1})
where ((x_1, y_1)) and ((x_2, y_2)) are points on the line.
- Positive Slope: The line rises from left to right.
- Negative Slope: The line descends from left to right.
- Zero Slope: The line is horizontal.
- Undefined Slope: The line is vertical.
Slope Examples
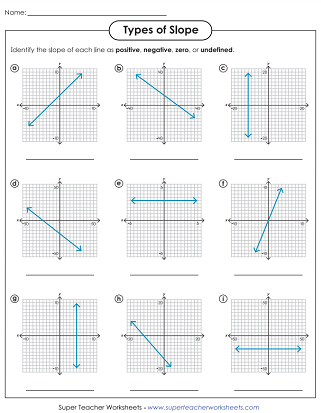
Let’s review some examples to solidify your understanding:
- Example 1: Calculate the slope between the points (2, 3) and (5, 8).
- Example 2: Determine the slope of the line that passes through the points (1, -2) and (3, -2).
- Example 3: Find the slope of a vertical line passing through the points (4, 7) and (4, 11).
Here’s how:
Slope ( m ) = (\frac{8 - 3}{5 - 2}) = (\frac{5}{3})
📝 Note: Always subtract in the same order, subtract the y-values first and then the x-values.
The calculation will be:
Slope ( m ) = (\frac{-2 - (-2)}{3 - 1}) = (\frac{0}{2}) = 0
This indicates the line is horizontal with zero slope.
Since both x-values are the same, the calculation would result in division by zero:
Slope ( m ) = (\frac{11 - 7}{4 - 4}) = undefined
The slope here is undefined because the line is vertical.
Slope Formula in Real-Life Applications

Slope is not just a theoretical concept; it’s widely used in practical scenarios:
- Engineering: In constructing roads, bridges, or even in building design, engineers need to calculate slope to ensure stability and efficiency.
- Finance: Slope can represent rates of return or growth rates in investments.
- Economics: Economists use slope to analyze supply and demand curves, reflecting how changes in one variable affect another.
Slope and the Y-Intercept
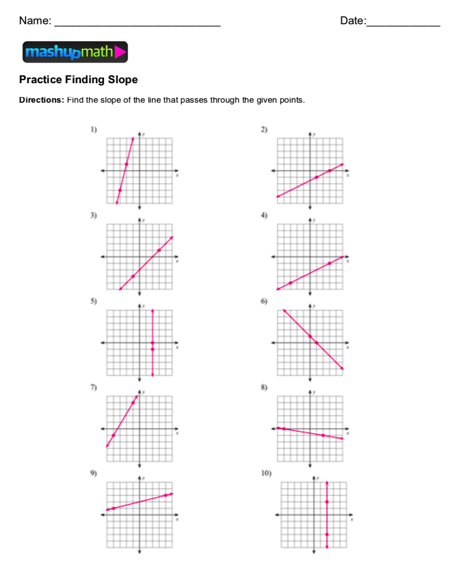
The slope-intercept form of a line equation is crucial for graphing and interpreting lines:
Y = mx + b
Here, m is the slope, and b is the y-intercept, where the line crosses the y-axis. Let’s look at how slope impacts the graph:
- High Positive Slope: The line is steep, rising sharply from left to right.
- Low Positive Slope: The line has a gentle incline.
- Negative Slope: The line slopes downward from left to right, the steeper the slope, the sharper the descent.
- Zero Slope: A horizontal line where the y-value does not change.
- Undefined Slope: A vertical line where the x-value does not change.
Common Misconceptions About Slope

Here are some common errors to avoid:
- Ignoring Direction: Remember that slope also indicates direction (upward or downward movement of the line).
- Switching Coordinates: Always take the difference in the same order (subtracting the first y-value from the second, and the first x-value from the second).
- Zero vs. Undefined: Be cautious with the difference; zero slope means horizontal, while undefined means vertical.
Slope in Different Coordinate Systems

While we’ve discussed slope in the Cartesian coordinate system, other coordinate systems also exist:
- Polar Coordinates: Here, slope is derived from the angle (\theta), where the slope ( m ) = tan((\theta)).
- Three-Dimensional Space: In 3D, slope becomes more complex, involving partial derivatives or the dot product.
The wrap-up: Understanding slope is not just about calculating it; it's about comprehending the underlying relationships between variables. Slope provides insight into trends, gradients, and the very nature of relationships in mathematical functions. This guide has covered various aspects of slope, from basic definitions and calculations to its applications in real life and beyond traditional 2D geometry. Whether you're an engineer, a student, or simply someone intrigued by math, mastering the concept of slope opens up numerous analytical and problem-solving avenues in both academic and professional contexts.
What does the slope indicate about a line?

+
Slope indicates the steepness and direction of a line, telling us how much the y-value changes per unit increase in the x-value.
How do I know if a slope is positive or negative?

+
A positive slope means the line rises from left to right; a negative slope means it descends from left to right.
Can the slope of a line be undefined?

+
Yes, the slope is undefined when the line is vertical because the calculation involves division by zero (the x-difference is zero).