5 Steps to Master Slope Point Form: Worksheet Included

Understanding and applying the slope point form is a fundamental skill in algebra, crucial for graphing linear equations and solving real-world problems. Whether you're a student, an educator, or just someone interested in math, mastering this concept can elevate your mathematical understanding significantly. Here, we delve into the 5 Steps to Master Slope Point Form, including a comprehensive worksheet to help solidify your grasp.
Step 1: Understanding the Basics of Slope Point Form

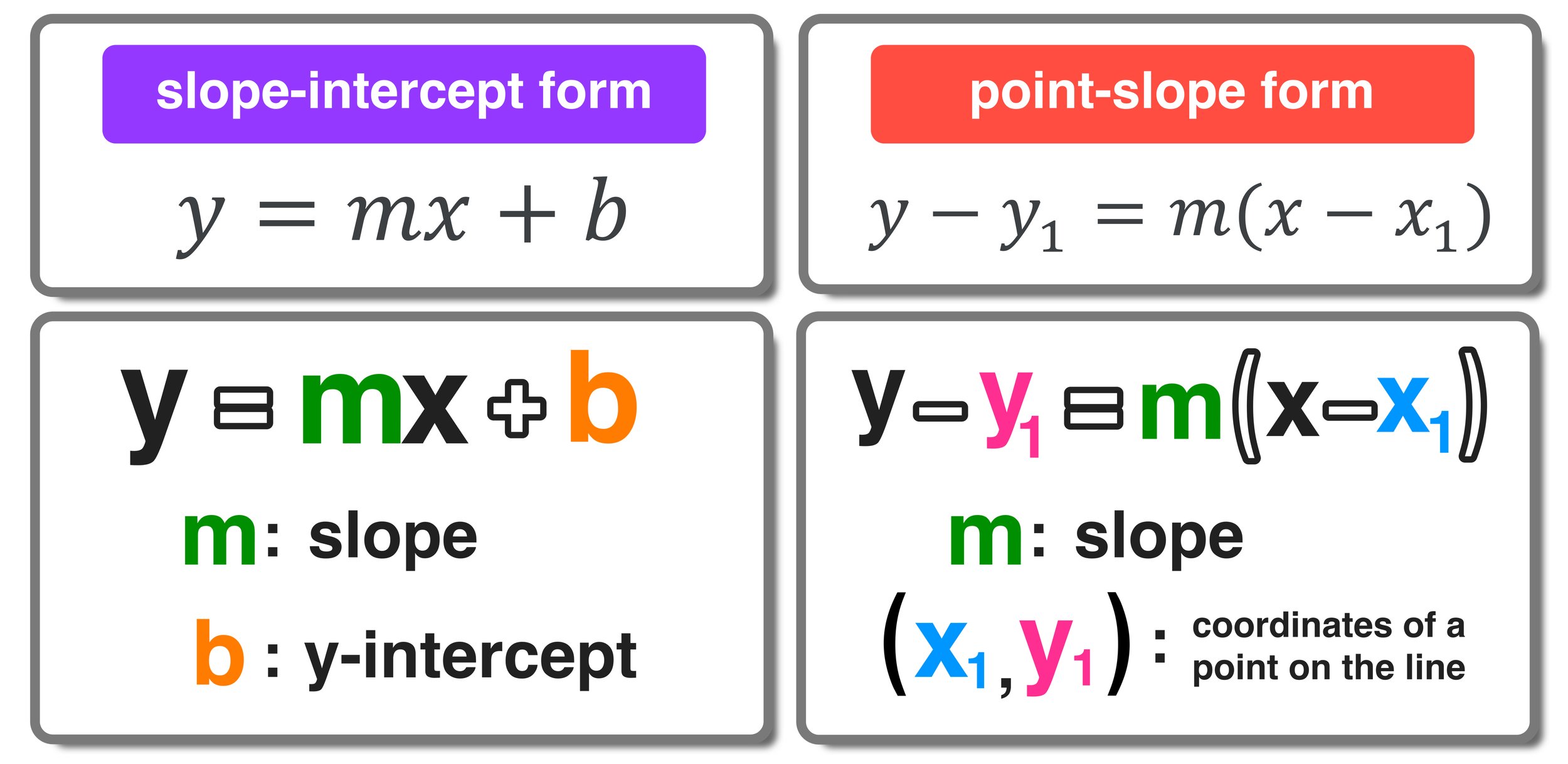
The Slope Point Form, often denoted as y - y₁ = m(x - x₁), where m is the slope and (x₁, y₁) is a point on the line, provides a quick way to write the equation of a line given its slope and a point through which it passes. Here are key components:
- Slope (m): The ratio of the vertical change to the horizontal change between any two points on a line.
- Point (x₁, y₁): Any point on the line you can use to determine the equation.

Step 2: How to Use Slope Point Form

To apply Slope Point Form, follow these steps:
- Identify the slope: This can be given directly or computed using another point if necessary.
- Choose a point: Use the coordinates of a point the line passes through.
- Substitute values into the formula: Replace m, x₁, and y₁ with the known values.
- Solve for y: Rearrange if necessary to isolate y to form the equation of the line.
🌟 Note: Always ensure the slope is consistent when using multiple points or given data. If there's an inconsistency, review the problem or the given information.
Step 3: Visualizing Slope Point Form with Graphing

Graphing is a fantastic way to understand the Slope Point Form visually:
- Plot the point (x₁, y₁) on a coordinate plane.
- Draw a slope line using m; for instance, if m = 2⁄3, you move up 2 units and over 3 units.
- Draw a straight line through this point to represent the line’s equation.

Step 4: Practice with a Worksheet

To truly master Slope Point Form, practice is essential. Here is a simple worksheet to help:
| Given Slope (m) | Given Point | Write Equation in Slope Point Form |
|---|---|---|
| 2 | (1, -3) | Let’s derive this together! |
| -1 | (4, 2) | Your Turn! |
| 1⁄2 | (-2, 7) | Try this one! |

Step 5: Advanced Applications
Once the basics are clear, you can tackle more complex problems:
- Intersecting lines: Determine the point of intersection of two lines using their equations in Slope Point Form.
- Parallel and Perpendicular lines: Use the properties of slopes to find equations of lines with given conditions.
- Real-world problems: Apply Slope Point Form to scenarios involving rates of change, like cost analysis, speed of travel, etc.
🔎 Note: When dealing with real-world scenarios, ensure to check the units and context to maintain accuracy in your calculations.
By following these steps and actively practicing with the included worksheet, you're on your way to mastering the Slope Point Form of a line. This method not only helps in understanding the connection between algebra and geometry but also simplifies various mathematical operations related to lines. Keep exploring, practicing, and applying these concepts to unlock deeper insights into linear equations and their applications.
What is Slope Point Form?

+
Slope Point Form is an equation for a line where you are given a point (x₁, y₁) on the line and the slope (m), expressed as y - y₁ = m(x - x₁).
Why use Slope Point Form over other forms?

+
It’s particularly useful when you have the slope and a point but don’t need to convert to standard form or slope-intercept form immediately.
How can I practice using Slope Point Form?

+
Practice with online math tools, use the worksheet provided, or engage with practice problems from textbooks and workbooks.
Can I find the equation of a line with only one point?

+
Yes, but you would also need the slope or another point to determine the unique line passing through that point.
What are some real-world uses for Slope Point Form?

+
Examples include analyzing growth rates, predicting market trends, understanding climate change data, or calculating cost based on varying quantities.