Slope Intercept Mastery: Essential Practice Worksheets
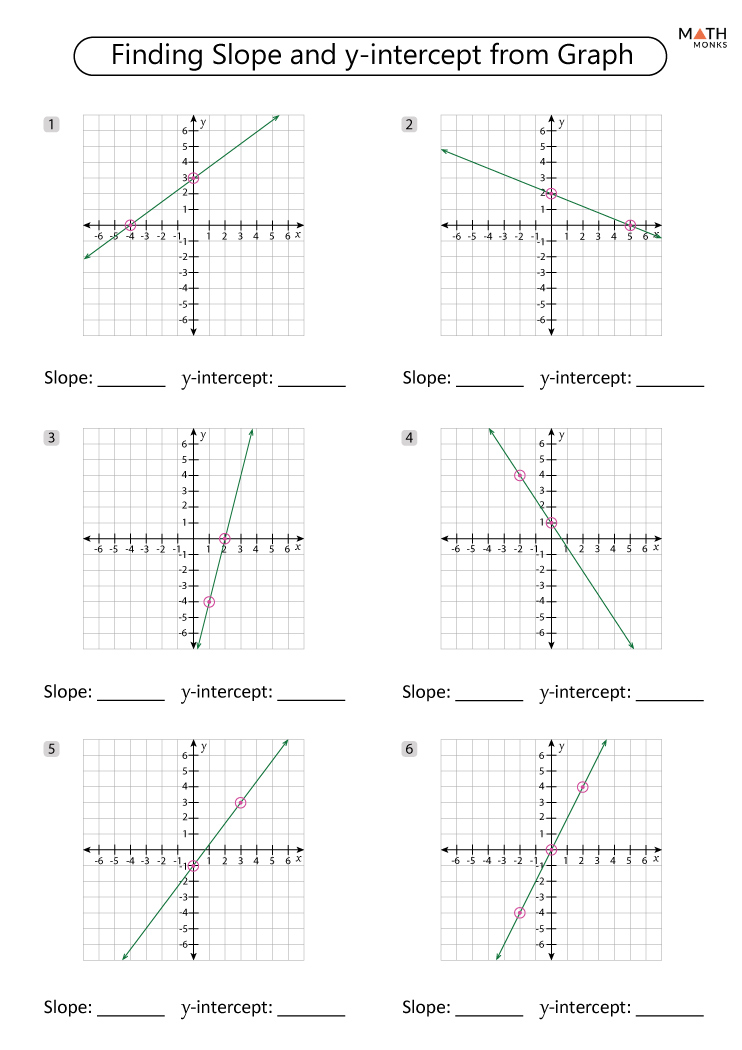
Understanding slope-intercept form is foundational for anyone studying algebra, providing a structured way to analyze linear equations and understand graphical representations. This blog post is designed to guide you through the process of mastering the concept of slope-intercept form with practical exercises, tips, and techniques to enhance your learning experience.
Why Slope-Intercept Form Matters

The slope-intercept form, represented as y = mx + b, where m is the slope and b is the y-intercept, is more than just a formula. It’s a tool that:
- Helps in visualizing how lines relate to each other on the coordinate plane.
- Allows for quick calculations to determine how steep a line is or where it crosses the y-axis.
- Provides a framework for solving linear equations, understanding their intersections, and exploring linear relationships in real-world applications.
Getting Started with Slope-Intercept Form

Let’s explore the components of the slope-intercept form:
| Component | Definition |
|---|---|
| m | The slope or gradient of the line, indicating how much y increases as x increases. |
| b | The y-intercept, where the line crosses the y-axis when x equals zero. |

Practical Exercises to Master Slope-Intercept

To master slope-intercept form, practice is key. Here are some exercises you can work through:
Identifying Slope and Y-Intercept

- Exercise: Given equations, identify m and b.
📌 Note: Remember to rearrange the equation into the form y = mx + b if necessary.
Graphing Lines

- Exercise: Plot lines using their slope and y-intercept.
📌 Note: Use graph paper for precision, and always label your axes.
Converting Between Forms

- Exercise: Convert standard form Ax + By = C to slope-intercept form.
📌 Note: Solving for y will be your main task here.
Determining Parallel and Perpendicular Lines

- Exercise: Find equations of lines parallel or perpendicular to given lines.
📌 Note: Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals.
Real-World Applications

Understanding slope-intercept form has practical applications:
- Cost Analysis: To determine profit or loss, understanding how costs change with respect to the number of units produced is vital.
- Physics: For example, in velocity-time graphs, the slope gives the acceleration while the intercept represents initial velocity.
- Economics: Supply and demand curves often use linear equations to model market behavior.
Working through these applications reinforces the real-world relevance of algebra, making the learning process more engaging and memorable.
Common Mistakes to Avoid

Here are some common pitfalls students fall into when learning slope-intercept form:
- Confusing slope with y-intercept.
- Overlooking the importance of solving for y to get the equation into proper form.
- Failing to recognize the significance of the sign of m (positive or negative) in terms of the line’s direction.
Strategies for Effective Learning

To truly master slope-intercept form, consider these learning strategies:
- Practice Regularly: Like any skill, regular practice is crucial for retaining and understanding concepts.
- Visualize: Graph the lines you work with to internalize how the equation corresponds to the graph.
- Link Concepts: Make connections between slope-intercept form and other algebraic concepts like linear inequalities, systems of equations, and functions.
By incorporating these strategies, you'll find that your understanding and proficiency with slope-intercept form will improve significantly.
In wrapping up, mastering slope-intercept form is not just about memorizing a formula; it's about understanding how linear relationships are modeled, how to analyze and graph them effectively, and applying this knowledge to real-world scenarios. Whether you're calculating profit margins, analyzing physical phenomena, or navigating economic models, slope-intercept form is an indispensable tool in your mathematical toolkit.
What is the difference between slope and y-intercept?

+
The slope (m) in the equation y = mx + b represents the steepness of the line, or how much y changes for each unit increase in x. Conversely, the y-intercept (b) is the point where the line intersects the y-axis, indicating the value of y when x is zero.
How do I convert an equation from standard form to slope-intercept form?

+
To convert from the standard form Ax + By = C to slope-intercept form:
- Isolate the y-term on one side of the equation.
- Divide through by the coefficient of y to get y = mx + b.
Why is the sign of the slope important?

+
The sign of the slope (m) indicates the direction of the line:
- A positive slope means the line ascends from left to right.
- A negative slope means the line descends from left to right.
- A zero slope represents a horizontal line, indicating no change in y with respect to x.