5 Simple Tricks to Master Slope Intercept Form Quickly

Understanding and mastering the slope intercept form is pivotal for students exploring the world of algebra. Slope intercept form, often written as y = mx + b, is not only a fundamental equation in algebra but also essential in various fields like engineering, physics, and economics. By employing five simple yet effective techniques, you can quickly become adept at using and applying the slope intercept form.
Understanding the Components

Before diving into the tricks, it’s crucial to comprehend what each part of the equation signifies:
- m - The slope, which tells us how steep the line is and its direction.
- b - The y-intercept, where the line cuts the y-axis.
💡 Note: Remembering what each variable stands for will make the following tricks easier to grasp.
Trick 1: The Ladder Method for Finding Slope

Visualize a ladder with rungs. Here’s how to use it:
- Pick two points on the line, say (x1, y1) and (x2, y2).
- Imagine each point as a rung on a ladder. Count the number of rungs you move up or down (Δy) and left or right (Δx).
- Calculate the slope by dividing Δy by Δx.

📝 Note: The ladder method is particularly useful when you can visualize the line or have a graph in front of you.
Trick 2: Use the Equation for Y-Intercept
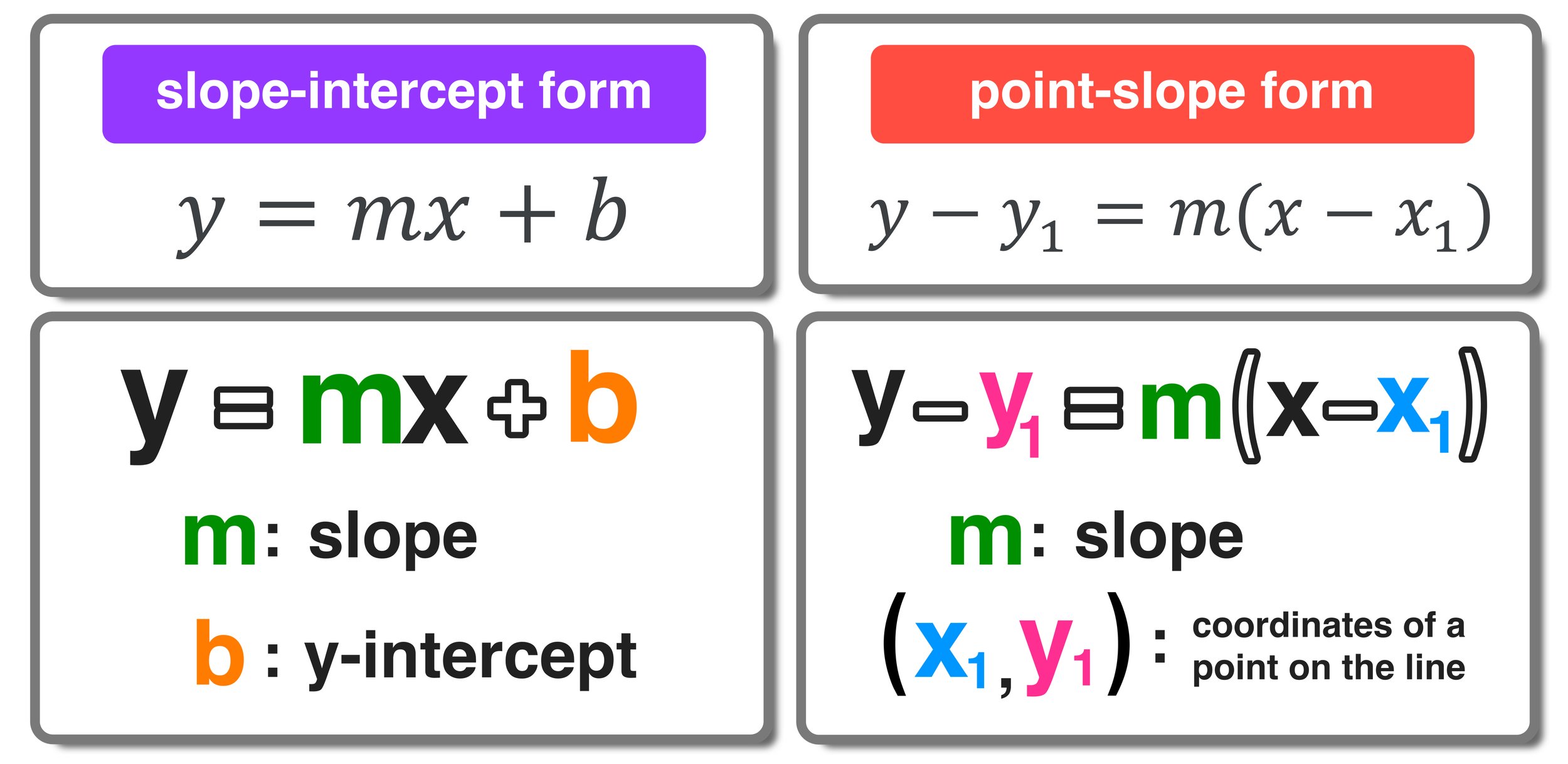
If you have the slope m and a point on the line (x, y), you can use the equation:
y - y1 = m(x - x1)
Here’s how:
- Plug in your known values for m, x, and y.
- Solve for b, the y-intercept.
💡 Note: This trick saves time as you directly derive the y-intercept from any given point on the line.
Trick 3: Spotting Slope-Intercept Form in Different Equations

Many equations can be manipulated into slope intercept form. Here are some examples:
| Original Equation | Converted to Slope-Intercept Form |
|---|---|
| 3x - 2y = 6 | y = (3⁄2)x - 3 |
| x = -4y + 5 | y = -1/4x + 5⁄4 |

When converting:
- Isolate y on one side of the equation.
- Identify the new values for m and b.
🔍 Note: Not all linear equations are presented in slope intercept form; recognizing and converting them is key to mastering algebra.
Trick 4: Graphing from Slope and Y-Intercept

Using m and b directly simplifies graphing:
- Plot the y-intercept b on the y-axis.
- Using the slope m (where m = Δy/Δx), move from the y-intercept to create your next point.
- Draw the line connecting these points.

💡 Note: This method is especially effective for quickly sketching or verifying the accuracy of an equation on a graph.
Trick 5: Real-World Applications

One of the best ways to master slope intercept form is by seeing it in action:
- Cost Analysis: Track fixed costs (y-intercept) and variable costs (slope) of a product.
- Physics: Understand velocity (where slope is acceleration) or any linear relationship.
- Economics: Analyze supply and demand curves, where slope represents elasticity.
By applying these scenarios, you reinforce your understanding through context.
🌎 Note: Real-world examples solidify your grasp of algebraic concepts, making them memorable and relevant.
The journey to mastering the slope intercept form is both practical and enriching. These five tricks are your stepping stones to conquer algebra with confidence:
- Visualize slopes using the ladder method.
- Directly find y-intercepts with known points.
- Transform equations into slope intercept form effortlessly.
- Graph lines quickly and accurately.
- Apply algebra in real-life scenarios to cement your learning.
Remember, practice is your ally in this journey. By incorporating these tricks into your study routine, you'll not only excel in exams but also gain a deeper appreciation for how linear relationships shape our world.
What is slope in real life?

+
Slope represents the rate of change in various fields. For example, in road construction, slope determines the steepness of a road. In business, it can show the rate at which costs or profits change with the number of items produced.
Can slope intercept form be used in 3D?

+
While the basic slope intercept form deals with 2D linear equations, similar principles can be extended to 3D planes, but it involves understanding partial derivatives and equations of planes in 3D space.
How do I know if I have the correct slope?

+
Verify the slope by plotting points from the equation or by using the given points to check if the calculated slope holds true. Additionally, if you’re solving for slope from an equation, use algebraic manipulation to ensure it matches the slope-intercept form.