5 Easy Steps to Master Slope Intercept Form

Understanding Slope Intercept Form

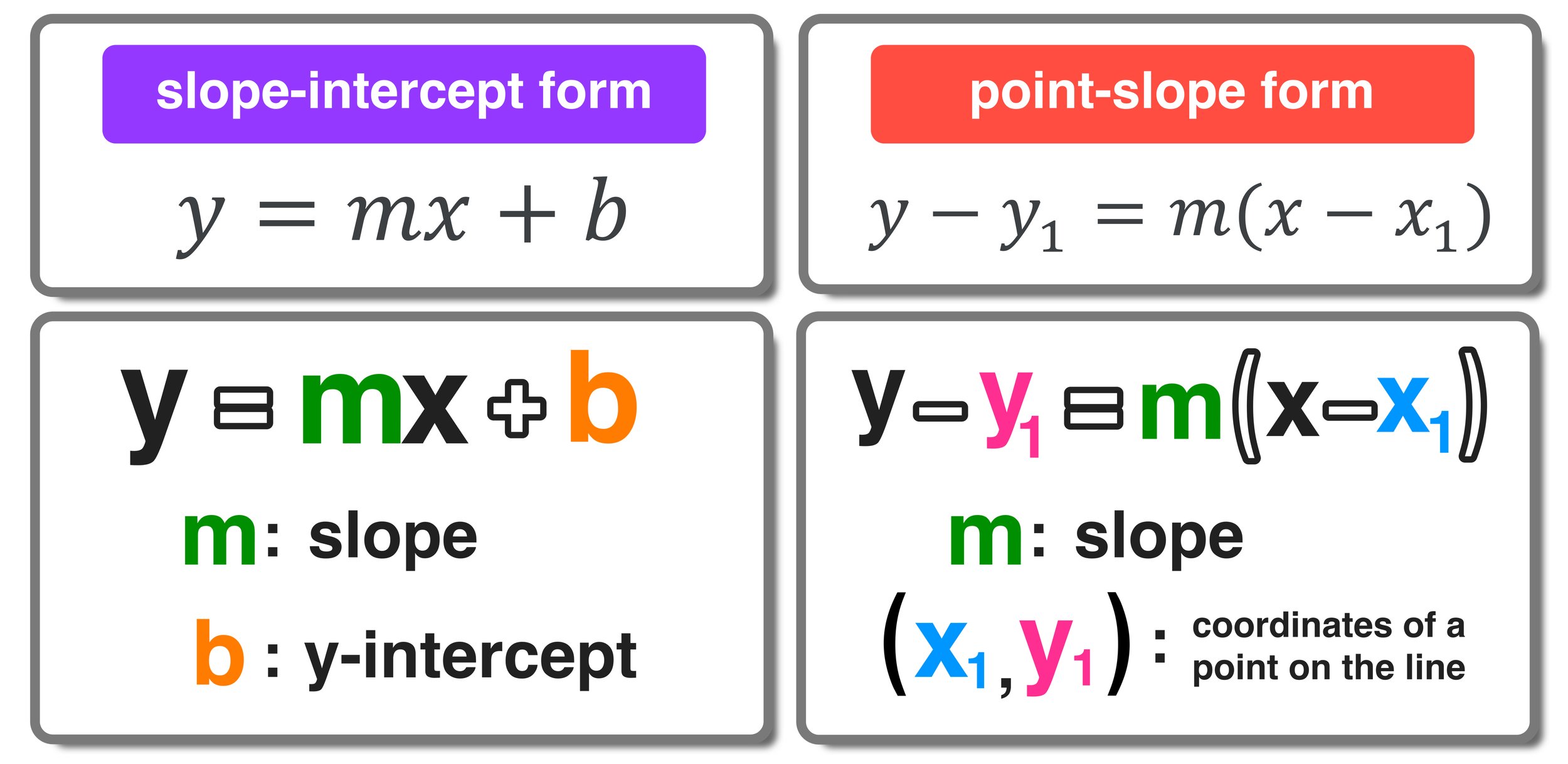
The slope intercept form is a way to express a linear equation in the form of y = mx + b, where:
- m represents the slope of the line, which indicates how steep the line is and in what direction it is slanting.
- b represents the y-intercept, which is the point where the line crosses the y-axis.
Why Master Slope Intercept Form?

Learning to use slope intercept form offers numerous benefits:
- It provides a clear visualization of the line’s characteristics, helping in graph plotting.
- It’s essential for algebra, calculus, and real-world problem-solving.
- It simplifies comparing different lines and understanding their relationship.
Step 1: Identifying Slope and Y-Intercept from an Equation

To master slope intercept form, you first need to recognize these components in an equation:
- Given an equation like y = 2x + 3, identify m = 2 as the slope, and b = 3 as the y-intercept.
🔍 Note: Remember, if the equation is not in slope-intercept form, you must rearrange it to make it so.
Step 2: Graphing a Line Using Slope Intercept Form

Graphing a line in slope intercept form involves:
- Plotting the y-intercept on the y-axis (b).
- Using the slope (m) to find additional points, stepping up or down by the rise and moving left or right by the run.
| Equation | Slope (m) | Y-Intercept (b) | First Point | Second Point |
|---|---|---|---|---|
| y = 2x + 3 | 2 | 3 | (0, 3) | (1, 5) |

Step 3: Converting Equations to Slope Intercept Form

Not all linear equations will come in slope intercept form:
- To convert any linear equation into this form:
- Isolate y on one side of the equation.
- Ensure the coefficient of x is not negative.
For example, take 3x - 2y = 6:
- Subtract 3x from both sides to get -2y = -3x + 6.
- Divide by -2 to isolate y, giving y = 1.5x - 3.
Step 4: Solving for Slope and Y-Intercept from Points

If you’re given two points, you can calculate the slope and then use one of the points to find the y-intercept:
- Calculate the slope with m = (y2 - y1) / (x2 - x1).
- Substitute this slope and the coordinates of one of the points into y = mx + b to solve for b.
Step 5: Practical Applications
Slope intercept form has many real-world applications:
- It's used in economics for demand and supply curves, where the slope indicates sensitivity.
- In physics, it can represent velocity versus time graphs.
- In business, it can model cost functions or predict future trends.
In wrapping up, understanding and mastering the slope intercept form allows for a greater grasp of linear functions, enhancing one’s ability to work with graphs, solve problems in various fields, and apply mathematical concepts to real-life scenarios. It’s a fundamental tool that, once mastered, opens doors to advanced mathematical reasoning and analytical thinking.
What if the equation doesn’t have a y-intercept?

+
If the y-intercept is not visible in the equation, it means the line either passes through the origin (b = 0), or it might be a special case like a vertical line, which doesn’t have a y-intercept but instead has an undefined slope (x = constant).
Can a line have a negative slope?

+
Yes, lines with a negative slope are slanting downward to the right. This indicates an inverse relationship between the variables x and y.
How do I find the equation of a line if I only know the slope?

+
You need at least one point (x, y) through which the line passes. With the slope (m) and a point, you can use the slope formula to find the equation.