Master Slope Calculation with Two Points Worksheet

When it comes to understanding mathematical concepts, especially those related to geometry and algebra, slope calculation stands out as a fundamental skill. Whether you are plotting graphs, determining the gradient of a line, or dealing with real-world applications like elevation changes or financial trends, mastering the calculation of slope with two given points is invaluable. This post will guide you through the process step by step, ensuring you understand not just how to find the slope but also why it's important in various contexts.
Understanding Slope

The slope, often denoted as ’m’, represents the steepness or inclination of a line. It gives an indication of how much ‘y’ changes for every unit change in ‘x’. Here’s how you calculate it:
- Identify two points on a line, say (x₁, y₁) and (x₂, y₂).
- Use the slope formula: m = (y₂ - y₁) / (x₂ - x₁)
Step-by-Step Guide to Calculating Slope

Here’s how you can apply this formula to find the slope:
1. Identify the Points
First, you need to know the coordinates of two points on the line. For example, let’s take the points A(2,5) and B(6,9).
2. Plug into the Formula
Substitute these coordinates into the slope formula:
m = (9 - 5) / (6 - 2)
m = 4 / 4
m = 1
So, the slope of the line passing through A and B is 1.
3. Interpretation
A slope of 1 means that for every unit you move to the right along the x-axis, you move one unit upward along the y-axis. This line has a positive and moderate slope.
Practical Applications of Slope

Calculating the slope isn’t just an academic exercise; it has real-world applications:
1. Elevation Changes

In hiking, for instance, understanding slope helps in assessing the difficulty of a trail. If the slope is steep, you might expect a more challenging hike.
2. Finance

Financial analysts use slope to determine trends in stock prices or investment returns over time, where a positive slope indicates growth, and a negative one indicates decline.
3. Engineering

Engineers use slope to design infrastructure like roads, ramps, and buildings to ensure safety and efficiency in construction.
4. Art and Design

In graphic design or art, knowing the slope can help in creating balanced compositions or optical illusions through perspective.
Worksheet for Slope Calculation

Let’s engage with a worksheet to practice calculating the slope between different pairs of points:
| Points | Slope (m) |
|---|---|
| (2, 3) and (5, 7) | (7 - 3) / (5 - 2) = 4 / 3 |
| (-1, 4) and (3, -4) | (-4 - 4) / (3 - (-1)) = -8 / 4 = -2 |
| (0, 0) and (10, 15) | (15 - 0) / (10 - 0) = 15 / 10 = 3 / 2 |
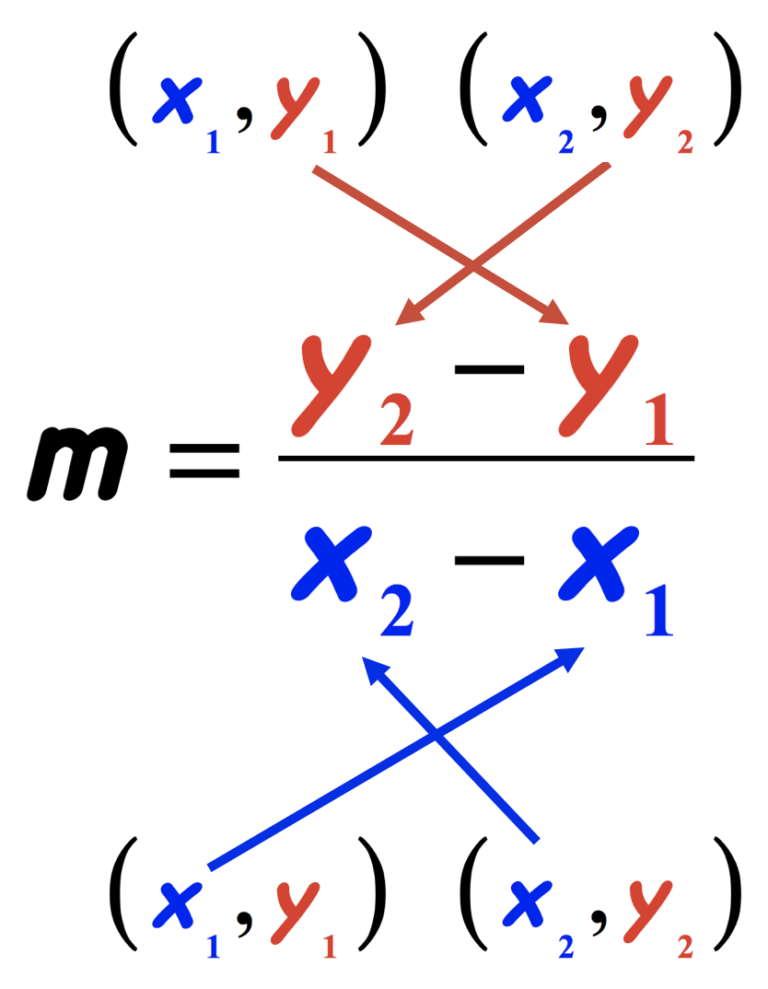
💡 Note: Negative slopes indicate a downward trend or descent, while positive slopes indicate an upward trend or ascent.
Enhancing Your Skills with Slope

To further enhance your understanding and proficiency in calculating slope:
- Use visualization: Graph the points and the line to get a visual representation of the slope.
- Understand zero and undefined slopes: A slope of 0 means a horizontal line (no change in y for any change in x), while an undefined slope refers to a vertical line (infinite change in y for no change in x).
- Practice with different scenarios: Try calculating slopes for lines that pass through the origin or for lines that are perfectly horizontal or vertical.
Understanding slope is more than just a mathematical formula; it's a tool for making sense of the world around us, from the gradients on a hill to the progression of data over time. By mastering the technique of calculating slope, you equip yourself with a lens to analyze and predict trends, design, and interpret various physical and abstract phenomena.
Advancing with Slope
Beyond basic calculations, the concept of slope can be integrated into more complex mathematical operations:
- Linear equations: The slope-intercept form of a line, y = mx + b, where ’m’ is the slope, allows you to write the equation of any line if you know any two points on it.
- Coordinate geometry: Understanding slopes helps in determining the nature of lines in a coordinate plane, their parallelism, or perpendicularity.
- Calculus: Derivatives, which are the instantaneous rate of change of a function, are essentially slopes of tangent lines at specific points.
With this foundation, you'll be ready to tackle more advanced concepts like finding the equation of lines or even dealing with curves and tangents in calculus.
In summary, slope calculation with two points is a gateway to a wide array of mathematical, scientific, and practical applications. It's an essential tool for anyone looking to understand or manipulate data, design physical structures, or analyze growth patterns. By practicing and applying the concepts discussed, you are well on your way to mastering this fundamental aspect of mathematics.
What does a zero slope mean?

+
A zero slope means the line is horizontal, indicating no change in ‘y’ for any change in ‘x’.
Can slope be negative?

+
Yes, a negative slope indicates that ‘y’ decreases as ‘x’ increases, signifying a downward trend or descent.
Why is slope important in real-life?

+
Slope helps us understand trends, predict outcomes, and design efficient structures. For example, in hiking, understanding slope can help assess the difficulty of a trail; in finance, it can track investment growth; and in engineering, it aids in designing safe road inclines or building structures.