Slope From a Table: Easy Worksheet Guide

Understanding slope is fundamental in mathematics, especially in algebra, where it quantifies the steepness of a line on a graph. This concept becomes tangible when working with data in tabular form. Whether you're a student grappling with calculus or an enthusiast exploring the basics of linear equations, this guide will walk you through how to find the slope from a table. Here, we'll detail the process, ensuring you grasp the nuances of slope calculation without getting lost in complex jargon or overwhelming math.
How to Find Slope From a Table


Here are the simple, step-by-step methods to calculate slope from a table:
Identifying Coordinates

The first step in calculating slope from a table involves:
- Selecting any two points from the table.
- Reading their corresponding values for the x- and y-axes.
Each point should be represented as (x1, y1) and (x2, y2). Let’s delve into an example:
| x | y |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
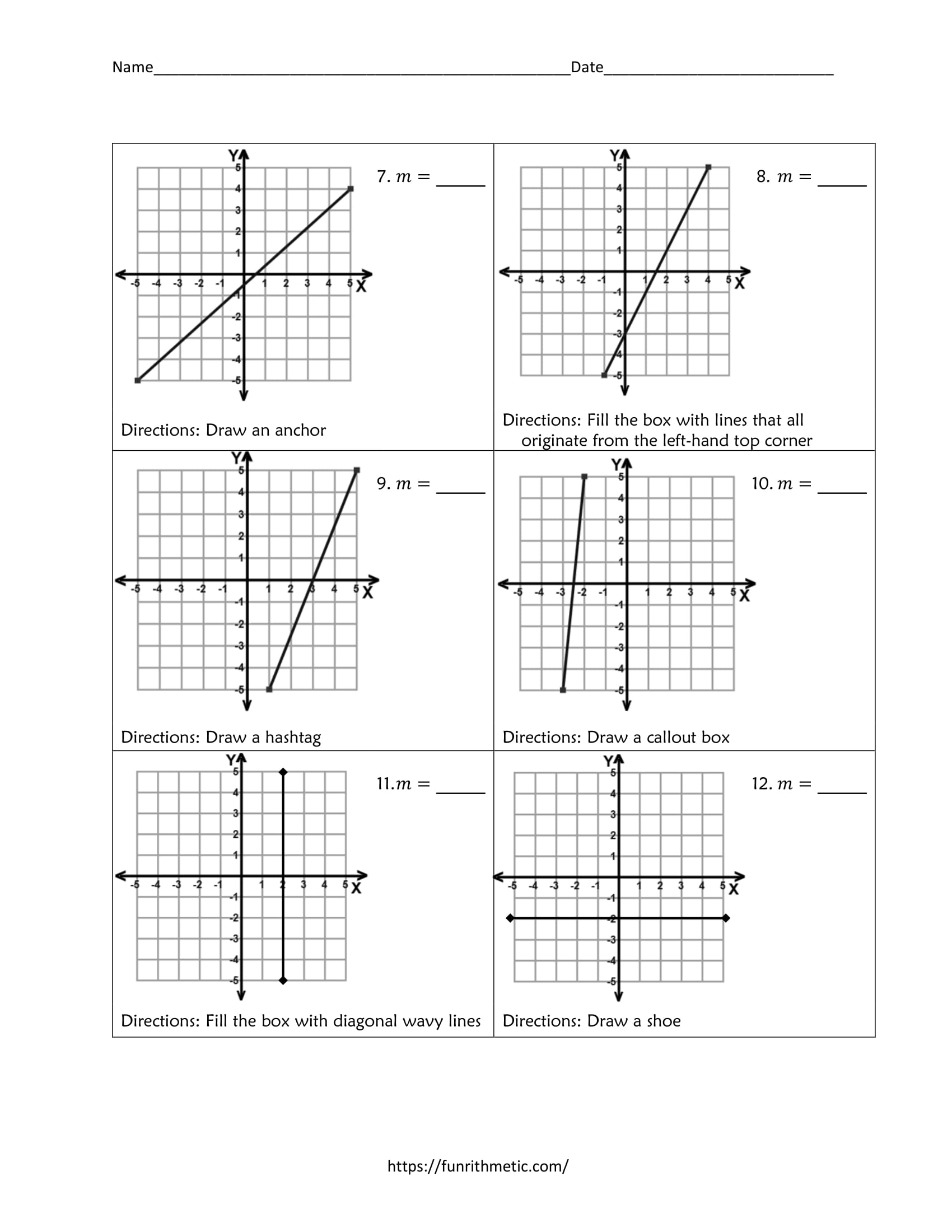
In this table, you can choose any two points, like (1,3) and (3,9).
Formula Application

Once you’ve identified your points, apply the slope formula:
- m = (y2 - y1) / (x2 - x1)
Let's calculate the slope for the example:
- Substitution: m = (9 - 3) / (3 - 1)
- Result: m = 6 / 2 = 3
Understanding the Slope

The slope value (m=3 in our example) tells us several key things:
- The line's steepness or gradient.
- If the slope is positive, the line ascends from left to right.
- If negative, the line descends.
Remember, slope is a measure of how much the y-value changes as x-value changes by 1. In our example, for every unit increase in x, y increases by 3 units.
📘 Note: When dealing with multiple points, selecting any pair of points will give the same slope for a linear relationship.
Verifying the Slope

Verify your calculations using multiple point pairs for accuracy:
Calculating Slope for Different Pairs

Take another pair of points like (2,6) and (3,9):
- m = (9 - 6) / (3 - 2) = 3 / 1 = 3
This reinforces the consistent slope of our linear equation.
📌 Note: When you see the same slope from different pairs, it confirms linearity in your data.
Practical Application of Slope
Understanding slope allows for:
- Predicting future values based on known data.
- Analyzing rate of change in various fields like economics, physics, or statistics.
- Designing linear models to fit data trends.
Common Mistakes to Avoid

Here are some pitfalls to watch out for:
- Not confirming linearity: Ensure the data points form a straight line before calculating slope.
- Arithmetic errors: Double-check your calculations.
- Ignoring the order of subtraction: Subtract y2 - y1 and x2 - x1 consistently.
When approaching slope from a table, remember these steps:
- Select any two points from the table.
- Use the slope formula with these points.
- Verify the slope with other pairs of points.
- Consider practical implications of the slope.
As we recap, the journey to understanding slope from a table involves recognizing the significance of this concept in broader mathematical and practical contexts. By learning to calculate and interpret slope, we empower ourselves to unlock deeper insights into data and how it evolves over time. This ability not only enriches our understanding of algebra but also equips us with a powerful tool for analysis in various domains of life, from financial forecasting to physical laws of motion.
How can I find slope if the table provides non-integer values?

+
The slope formula remains the same regardless of the values being integers or not. Simply use the given values for y2, y1, x2, and x1 and perform the subtraction and division as usual. Fractional or decimal numbers will still yield a valid slope.
Can I find the slope if my table has more than two points?

+
Yes, you can choose any two points from the table to calculate the slope. If the points form a linear relationship, the slope will be consistent across different pairs.
What if my slope calculation yields an undefined value?

+
An undefined slope indicates a vertical line where the difference between the x-coordinates (x2 - x1) is zero. In this case, you are dividing by zero, which in mathematics, is undefined.
How do I interpret a slope of zero?

+
A slope of zero implies a horizontal line where there is no change in y as x changes. This means the values of y are constant across all x values.
Is the slope always the same for all pairs of points on a straight line?

+
Yes, for any two points on a straight line, the slope will remain the same, confirming the linearity of the relationship between the variables.



