Mastering Sine and Cosine Graphing Made Easy
Understanding the Basics of Sine and Cosine Graphing
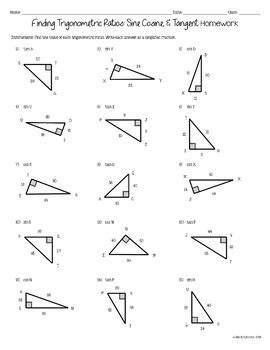
Sine and cosine graphing are fundamental concepts in mathematics, particularly in trigonometry. These graphs are essential in understanding various mathematical relationships and are used extensively in physics, engineering, and other fields. In this article, we will explore the basics of sine and cosine graphing, their differences, and provide a step-by-step guide on how to graph them.
The Sine Graph
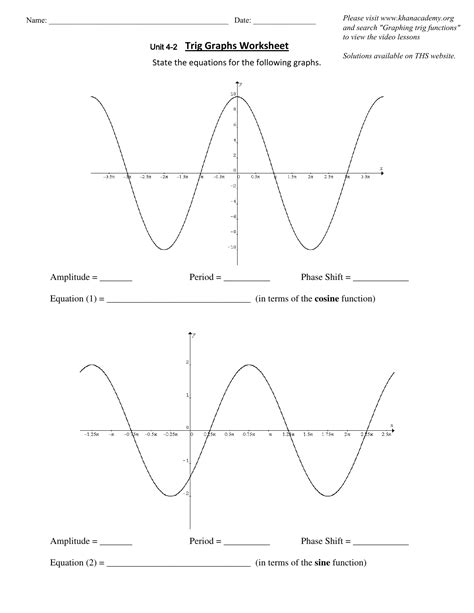
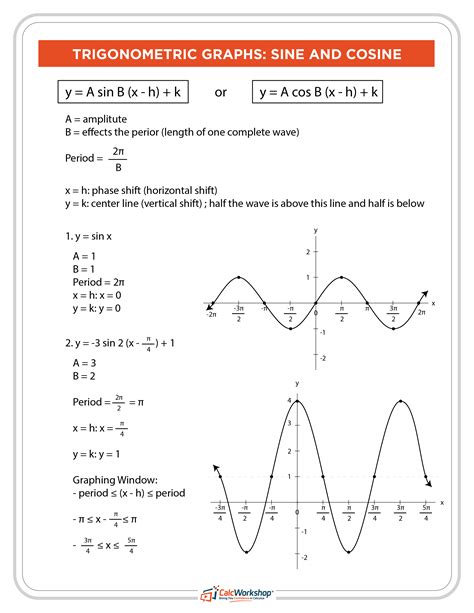
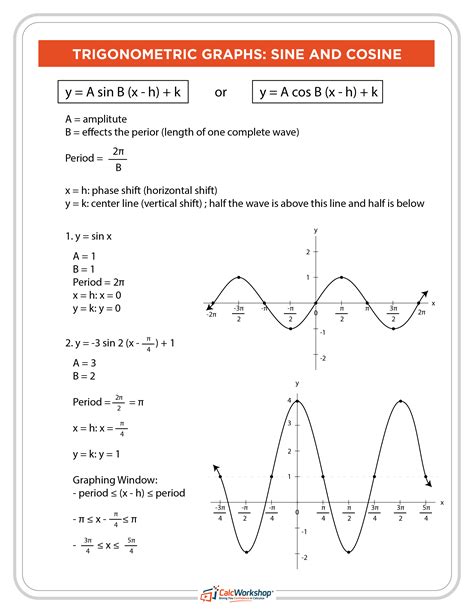
The sine graph, also known as the sinusoidal graph, is a periodic graph that oscillates between -1 and 1. It is a continuous, smooth, and curved graph that repeats every 360 degrees or 2π radians. The general equation of a sine graph is:
y = sin(x)
Where x is the angle in degrees or radians, and y is the corresponding sine value.
Key Features of the Sine Graph
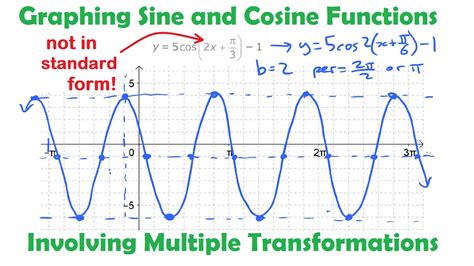
- Period: The sine graph has a period of 360 degrees or 2π radians, meaning it repeats every 360 degrees or 2π radians.
- Amplitude: The amplitude of the sine graph is 1, meaning it oscillates between -1 and 1.
- Phase Shift: The phase shift of the sine graph is 0, meaning it starts at the origin (0,0).
The Cosine Graph

The cosine graph is similar to the sine graph but has a phase shift of 90 degrees or π/2 radians. The general equation of a cosine graph is:
y = cos(x)
Where x is the angle in degrees or radians, and y is the corresponding cosine value.
Key Features of the Cosine Graph

- Period: The cosine graph has a period of 360 degrees or 2π radians, meaning it repeats every 360 degrees or 2π radians.
- Amplitude: The amplitude of the cosine graph is 1, meaning it oscillates between -1 and 1.
- Phase Shift: The phase shift of the cosine graph is 90 degrees or π/2 radians, meaning it starts 90 degrees or π/2 radians to the right of the origin.
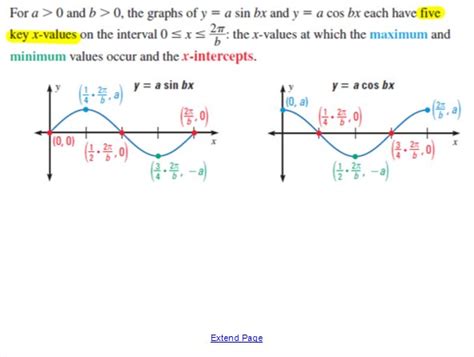
Graphing Sine and Cosine Functions
To graph sine and cosine functions, follow these steps:
- Determine the period: Identify the period of the graph, which is 360 degrees or 2π radians for both sine and cosine graphs.
- Identify the amplitude: The amplitude of both sine and cosine graphs is 1.
- Determine the phase shift: The phase shift of the sine graph is 0, while the phase shift of the cosine graph is 90 degrees or π/2 radians.
- Plot the graph: Start by plotting the graph at the origin (0,0) and then move 90 degrees or π/2 radians to the right for the cosine graph.
- Draw the graph: Draw a smooth, continuous curve that oscillates between -1 and 1.
📝 Note: When graphing sine and cosine functions, use a graphing calculator or software to ensure accuracy.
Common Applications of Sine and Cosine Graphing

Sine and cosine graphing have numerous applications in various fields, including:
- Physics: Sine and cosine graphs are used to describe the motion of objects, such as simple harmonic motion.
- Engineering: Sine and cosine graphs are used in the design of electronic circuits and filters.
- Navigation: Sine and cosine graphs are used in navigation systems, such as GPS.
Conclusion

Mastering sine and cosine graphing is essential for understanding various mathematical relationships and applications. By understanding the basics of sine and cosine graphing, you can apply these concepts to solve problems in physics, engineering, and other fields. Remember to use graphing calculators or software to ensure accuracy when graphing sine and cosine functions.
What is the period of the sine graph?
+
The period of the sine graph is 360 degrees or 2π radians.
What is the amplitude of the cosine graph?
+
The amplitude of the cosine graph is 1.
How do I determine the phase shift of the cosine graph?

+
The phase shift of the cosine graph is 90 degrees or π/2 radians.
Related Terms:
- free cosine sine tangent worksheet
- graphing sine function worksheet pdf
- graphing sine functions worksheet
- graphing sine and cosine quizlet
- graphing sine and cosine practice
- sin cos graph practice problems