Square Roots Simplified: Easy Worksheet Answers
Many students encounter difficulties when tackling square roots in their math curriculum. This comprehensive guide will demystify the process of simplifying square roots with easy worksheet answers, making the learning journey less daunting. Whether you're a student or a tutor, understanding these fundamentals will enhance your mathematical proficiency.
What are Square Roots?

In mathematics, a square root of a number x is another number y such that y × y = x. The symbol for square root is √, and it's denoted as √x. Here are some key points:
- The principal (non-negative) square root of x is denoted as √x.
- Each non-negative number has a unique non-negative square root.
- Negative numbers have imaginary square roots, which involves complex numbers.
Simplifying Square Roots
To simplify square roots, we often reduce them to a product of prime numbers. Here’s how you can approach this:
Step-by-Step Simplification Process:

Step 1: Factor the number inside the square root into its prime factors.
Step 2: For each pair of prime factors inside the square root, take one out.
Step 3: Multiply the factors taken out together, and leave the unpaired primes under the square root sign.
Here's an example:
- √50
- Factors of 50 are 2 × 5 × 5.
- Pull out a pair of 5s: √(5 × 5 × 2).
- Simplify to: 5√2.
✏️ Note: Remember, only pairs of identical factors can be simplified outside the square root.
Handling Complex Square Roots

What if the number inside the square root has both even and odd factors? Here's how to deal with them:
- Even Factors: These are pairs that simplify outside the square root.
- Odd Factors: These stay under the square root sign if there isn't a perfect square factor.
Let's look at √72:
- 72 = 2 × 2 × 2 × 3 × 3.
- Pull out the pairs: √(2 × 2 × (2 × 3) × 3).
- Simplify to: 6√2.
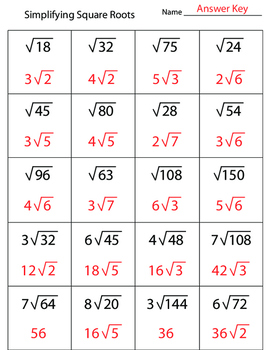
Worksheet with Answers

Let's provide some common square root problems and their answers:
| Problem | Steps | Answer |
|---|---|---|
| √36 | √(2 × 2 × 3 × 3) | 6 |
| √90 | √(2 × 3 × 3 × 5) | 3√10 |
| √18 | √(2 × 3 × 3) | 3√2 |
Advanced Techniques

For those looking for a deeper understanding:
- Pythagorean Theorem: When calculating the hypotenuse of a right triangle, you often need to square root the sum of squares.
- Estimating Square Roots: You can estimate the square root by sandwiching the number between two perfect squares.
- Using Logarithms: Logarithms can help find square roots without direct computation.
🔍 Note: Understanding these techniques can be crucial in higher math and real-world applications.
Practical Applications

Here's how square roots are used in daily life:
- Construction: Measuring distances and dimensions.
- Physics: Calculating forces, velocities, and distances.
- Finance: Interest rates and investment returns.
📝 Note: Recognizing the importance of square roots in real-life situations helps students relate math to their everyday experiences.
This guide has covered essential aspects of simplifying square roots, offering a straightforward pathway from basic to more advanced concepts. Whether for homework or classroom instruction, mastering these techniques will not only boost your math skills but also your ability to tackle practical problems in various fields. By following the provided steps, understanding the underlying principles, and practicing with the worksheet examples, you'll have a solid foundation to work with square roots with confidence.
How do you simplify the square root of a negative number?

+
Negative numbers do not have real square roots; instead, they have imaginary square roots. To simplify, you treat it as a positive number, then multiply by ‘i’, the imaginary unit.
Can I simplify a square root without factoring?

+
Yes, but it might be less intuitive. One method is using the ‘trial and error’ by finding the closest perfect squares or using a calculator for estimation.
What if the number under the square root has a decimal?

+
Treat the decimal as a fraction, simplify the square root of the numerator and the denominator separately, then convert back to a decimal if needed.
How does understanding square roots help in real life?

+
From measuring distances in construction to analyzing growth rates in finance, square roots are essential in various practical applications where proportions and geometric calculations are involved.



