Simplify Rational Expressions Worksheet - With Answers

Mastering the simplification of rational expressions can be a pivotal skill for students navigating algebra. Rational expressions, much like fractions, involve variables, and simplifying them helps in solving equations, factoring polynomials, and understanding more complex math concepts. In this article, we'll delve into the process of simplifying these expressions step-by-step, with examples and useful insights to ensure you grasp this topic fully.
Understanding Rational Expressions

A rational expression is a fraction where both the numerator and the denominator are polynomials. To simplify these, we need to understand how to factor polynomials and apply the rules of simplifying fractions. Here’s what you should know:
- The numerator and denominator must be simplified in tandem.
- Variables and constants are manipulated similarly to basic fractions.
- Always factor the numerator and denominator first.

Step-by-Step Guide to Simplifying Rational Expressions

To simplify a rational expression:
- Factor the Numerator and Denominator: This step is crucial as it prepares you for canceling common factors.
- Identify and Cancel Common Factors: If there are common factors in both the numerator and denominator, you can cancel them out.
- Reduce to Lowest Terms: After canceling, ensure the expression is in its simplest form.

🔔 Note: Always remember to check if the simplified form is still a valid rational expression (i.e., the denominator is not zero).
Example 1:

Consider simplifying (\frac{6x^2 + 3x}{3x}).
- Factor the numerator: (6x^2 + 3x = 3x(2x + 1))
- The expression becomes: (\frac{3x(2x + 1)}{3x})
- Cancel the common factor (3x) (assuming (x \neq 0)): (2x + 1)
Example 2:
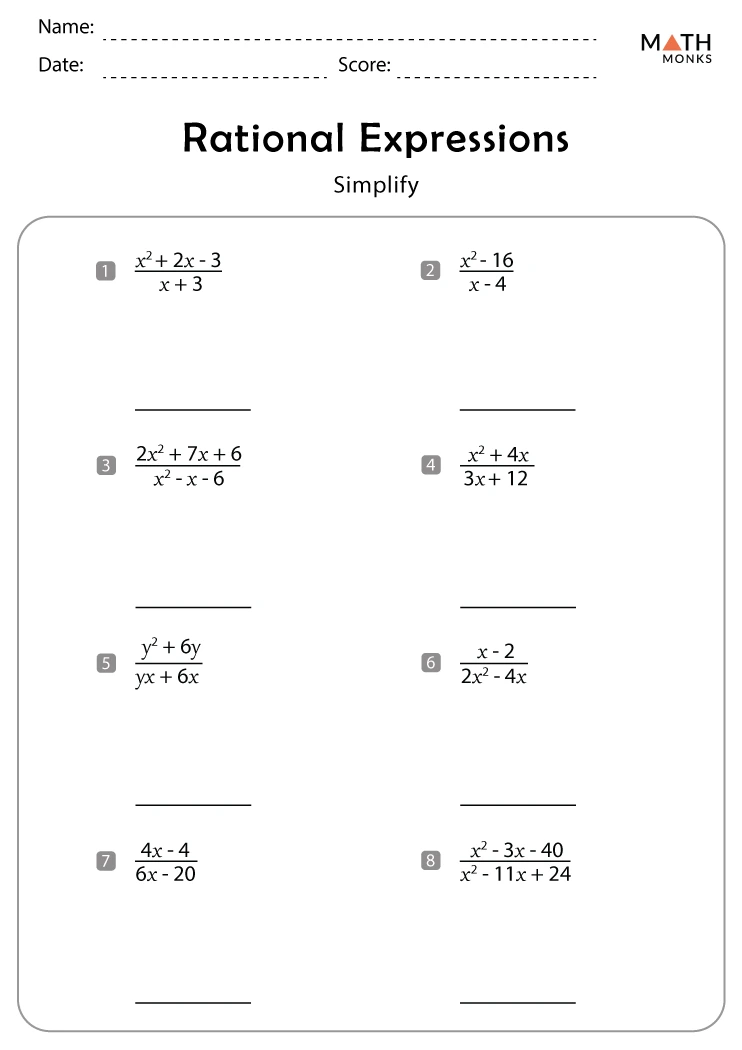
Let’s simplify (\frac{10x^2 - 5x}{10x}).
- Factor both the numerator and the denominator: (\frac{5x(2x - 1)}{5x})
- Cancel (5x) (assuming (x \neq 0)): (2x - 1)
🔄 Note: If there's no common factor, the expression is already in its simplest form.
Advanced Techniques for Simplifying Rational Expressions
Sometimes, simplifying rational expressions involves more than just basic factoring. Here are some advanced techniques:
- Expanding Binomials: When the numerator or denominator has squared terms, expanding can help.
- Identifying Difference of Squares: Look for patterns like (a^2 - b^2 = (a + b)(a - b)).
- Using Synthetic Division: If one polynomial is divided by another, synthetic division can find roots and factors.

Example 3:

Let’s simplify (\frac{x^3 + 3x^2 + 3x + 1}{x^2 - 1}).
- Notice the numerator is a perfect cube plus one, so factor as ((x+1)^3).
- The denominator can be factored as a difference of squares: ((x + 1)(x - 1)).
- The expression simplifies to (\frac{(x+1)^3}{(x+1)(x-1)}) or (\frac{x+1}{x-1}) (for (x \neq -1)).
Final Thoughts

The process of simplifying rational expressions is an exercise in problem-solving and critical thinking. It’s not just about following steps; it’s about recognizing patterns, understanding how factors relate, and knowing when an expression is in its simplest form. As you practice, your proficiency in recognizing factorable polynomials and applying simplification strategies will grow, aiding your math journey in algebra and beyond.
What does it mean to simplify a rational expression?

+
Simplifying a rational expression involves reducing it to its most basic form by factoring the numerator and denominator to remove common factors. The process is akin to reducing fractions, making the expression more manageable and easier to solve or work with.
How do I know if I’ve simplified a rational expression correctly?

+
Check your work by confirming that there are no common factors in the numerator and denominator left to cancel. Additionally, ensure that the simplified expression is valid (the denominator is not zero). If it’s not, you might have canceled a factor that is not common to both polynomials at that value of the variable.
Why is factoring important in simplifying rational expressions?

+
Factoring is the key to simplifying rational expressions because it allows you to identify and cancel common factors between the numerator and the denominator. Without factoring, you could miss opportunities to reduce the expression to its simplest form.
What are some common mistakes to avoid when simplifying rational expressions?

+
Some common mistakes include:
- Canceling terms instead of factors.
- Forgetting to check the domain restrictions after simplifying.
- Incorrect factoring or misidentifying common factors.
- Overlooking the importance of expanding binomials or recognizing special factoring patterns like the difference of squares.



