Mastering Simplifying Radicals: Your Ultimate Worksheet Guide

The process of simplifying radicals, often recognized by the square root symbol (√), might seem intimidating at first glance. However, with the right strategies and a bit of practice, simplifying these mathematical expressions can become not only manageable but also quite engaging. This ultimate worksheet guide aims to demystify radicals for students, educators, and anyone interested in mathematics. Here's how you can master simplifying radicals:
Understanding Radicals

Before diving into simplification, understanding what radicals are is crucial:
- Radicals are expressions that signify the root of a number, most commonly the square root.
- The square root of a number x is a value which, when multiplied by itself, equals x.
- Other roots exist, like cube roots, fourth roots, etc., but we’ll focus on simplifying square roots here.
An example to illustrate: the square root of 9 (√9) is 3, because 3 × 3 = 9.

Basic Simplification Techniques

The goal is to break down the number under the radical into its prime factors and then try to take out any pairs or repeated factors:
- Prime Factorization: Break the number down into its prime factors. If √48 needs simplifying, factor 48 as 2 × 2 × 2 × 2 × 3.
- Pairing Up: Every pair of identical factors can come out of the radical sign as one. In our 48 example, we have two pairs of 2, which equals 2 × 2 or 4.
- Final Result: Our simplified version of √48 would be 4√3, as the remaining 3 is not a perfect square.

Step-by-Step Worksheet for Radicals

| Problem | Prime Factorization | Pairs | Simplified Result |
|---|---|---|---|
| √8 | 2 × 2 × 2 | One pair of 2 | 2√2 |
| √24 | 2 × 2 × 2 × 3 | One pair of 2 | 2√6 |
| √72 | 2 × 2 × 2 × 3 × 3 | Two pairs of 2, one pair of 3 | 6√2 |

🔍 Note: This table provides examples but isn’t exhaustive. Practice with different numbers to master this skill.
Advanced Techniques

When dealing with more complex radicals or multiple radicals within the same expression, here are some advanced tips:
- Combining Radicals: Radicals can be combined like similar terms if they have the same radicand (the number under the square root). For example, 2√3 + 3√3 = 5√3.
- Multiplying Radicals: Multiplying radicals involves multiplying the numbers under the square roots. To multiply √a by √b, you get √(a × b).
- Dividing Radicals: When dividing, rationalize the denominator by multiplying both numerator and denominator by the conjugate of the denominator if necessary.
Practice and Repetition
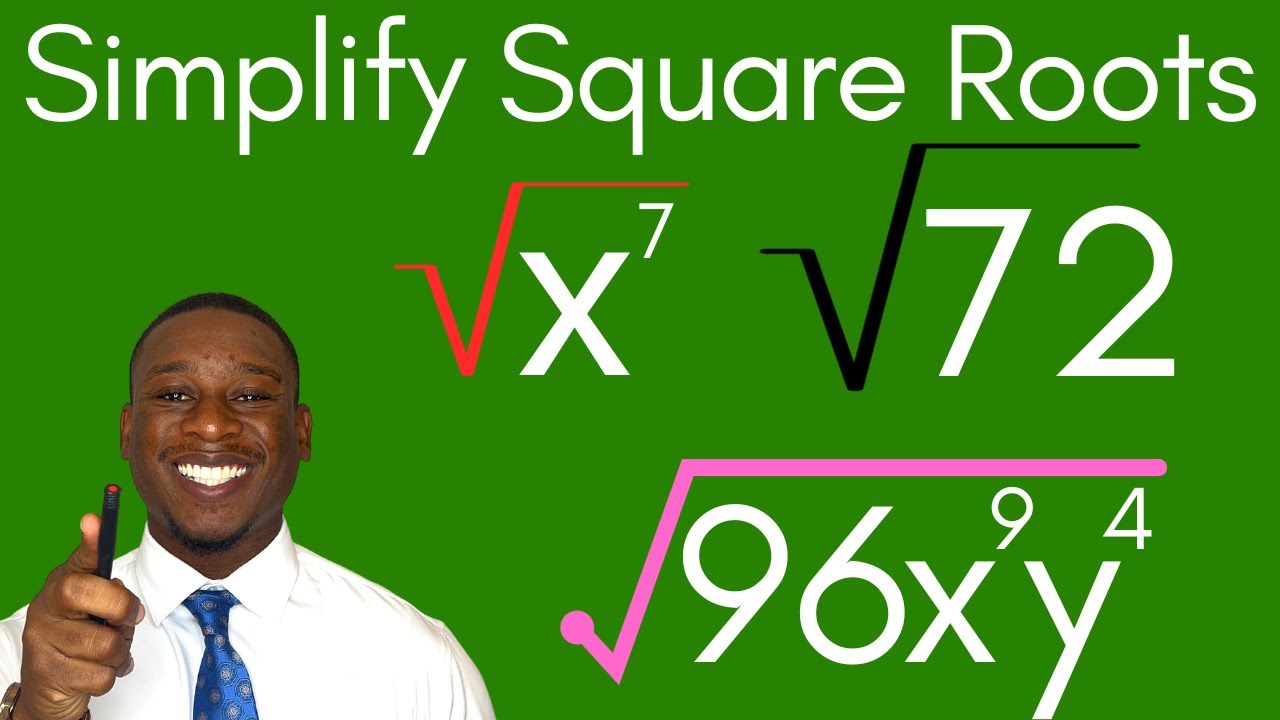
To truly master simplifying radicals:
- Make use of worksheets with diverse problems.
- Consider using software or online platforms that can generate countless radical problems.
- Find a study buddy or group for collaborative learning.
💡 Note: Consistency in practice leads to proficiency; make sure to revisit earlier exercises to reinforce your skills.
Real-World Applications

While radicals might appear to be abstract, they have real-world applications:
- Architecture: Calculating dimensions for certain geometric shapes often involves square roots.
- Physics: Radicals are present in formulas for velocity, acceleration, and force.
- Engineering: Engineers simplify complex expressions when designing systems or analyzing data.
🚀 Note: Understanding radicals can enhance your mathematical proficiency, making you more adept in various fields.
To sum up, mastering simplifying radicals not only improves your mathematical prowess but also connects you to real-world applications where these skills are invaluable. By following the structured steps, practicing consistently, and understanding the fundamentals of radicals, you pave the way for a smoother journey through advanced mathematics.
Why do we need to simplify radicals?

+
Simulating radicals makes expressions more manageable, reduces computation errors, and often simplifies further calculations involving these expressions.
What are the common mistakes when simplifying radicals?

+
Common mistakes include not factoring completely, incorrectly pairing factors, and mistakenly combining radicals with different indices or radicands.
Can radicals be simplified without prime factorization?

+
While prime factorization is the most common method, some shortcuts exist. For example, recognizing common squares (like 4, 9, 16) can help, but it’s less systematic than full factorization.
How can I remember the process of simplifying radicals?

+
Use mnemonics, practice regularly, and visualize the steps. Additionally, remember the basic principles like “pairs of identical factors come out of the radical sign.”
Can every number be simplified?

+
Every number can be written as a prime factorization, and this process can help in simplifying radicals to the greatest extent possible. However, not every number under a square root will simplify to an integer.