5 Essential Tips for Geometry Similarity Worksheets

Geometry is an essential part of mathematics education, where students learn about shapes, sizes, and the relationships between them. One crucial concept within geometry is similarity—the idea that two figures have the same shape but not necessarily the same size. Teaching and learning this concept effectively can be greatly aided by the use of similarity worksheets. Here are five essential tips to make the most out of geometry similarity worksheets.
Tip 1: Begin with Basic Concepts

Start your students' journey into similarity by ensuring they have a solid understanding of the foundational principles:
- Proportions: Explain how ratios between corresponding sides remain constant in similar figures.
- Similar Triangles: Introduce the AA (Angle-Angle), SAS (Side-Angle-Side), and SSS (Side-Side-Side) postulates.
- Scale Factors: Discuss how the scale factor determines the size relationship between figures.
Worksheets should be designed to reinforce these concepts through exercises that require students to identify similarities or differences in shapes.
Tip 2: Use Real-Life Applications

Real-life examples help students grasp why similarity is important. Include these in your worksheets:
- Enlarging or reducing images in graphic design.
- Map scale usage for travel or geography.
- Shadow lengths in relation to the height of objects.
Creating problems that show how similarity is applied in real-life situations makes learning more engaging and relevant.
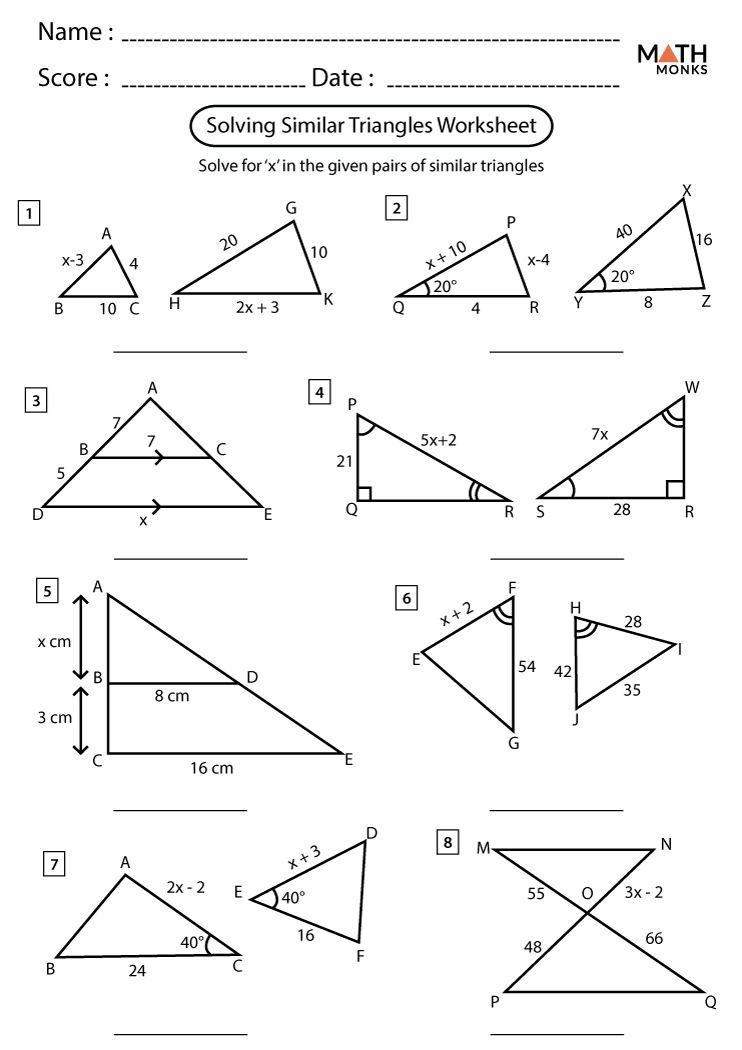
Tip 3: Incorporate Visuals and Diagrams

Since geometry is inherently visual, utilizing diagrams is crucial:
- Include multiple-choice questions with diagrams where students identify similar figures.
- Use color-coded diagrams to emphasize corresponding parts in similar shapes.
- Provide exercises where students draw similar shapes, given certain dimensions.
| Example Problem | What to Look For |
|---|---|
| Given triangles ABC and DEF, find the scale factor if AB = 6 and DE = 9. | Correct identification of corresponding sides; Understanding scale factor. |
| Are the triangles similar if the angles are 45°, 90°, 45° in both triangles? | Recognition of AA similarity postulate. |

Tip 4: Encourage Collaborative Learning

Utilize worksheets as tools for group activities:
- Partner students to solve problems together, fostering discussion.
- Create worksheet exercises where one student measures, and another calculates.
- Design activities where students explain their solutions to peers.
🌟 Note: Collaborative learning not only makes math fun but also helps students articulate their understanding, enhancing retention and application of concepts.
Tip 5: Feedback and Self-Assessment
Feedback is essential for learning:
- Include answer keys with detailed explanations.
- Encourage students to mark their work and understand their mistakes.
- Set up self-assessment sections where students can gauge their own progress.
Feedback and self-assessment empower students to take charge of their learning, recognizing where they excel and where they need more practice.
Geometry similarity worksheets, when thoughtfully designed and utilized, can significantly enhance students' understanding of this complex yet fascinating topic. By starting with basic concepts, applying real-life situations, incorporating visual aids, fostering collaboration, and providing meaningful feedback, educators can make learning about similarity both accessible and engaging.
To summarize, these key points are instrumental in effectively teaching similarity:
- Lay a foundation with basic principles of similarity.
- Bridge the gap between theory and practice with real-life applications.
- Use visual aids to clarify concepts visually.
- Promote peer-to-peer learning to deepen understanding.
- Encourage self-assessment to empower students in their learning journey.
Why is teaching similarity important in geometry?

+
Similarity helps students understand proportional relationships and scaling, which are critical for various fields like architecture, engineering, and even in daily life for applications like enlarging or reducing images or maps.
What are some effective ways to assess students’ understanding of similarity?

+
Assessment can include observation during group activities, traditional quizzes, homework assignments, and self-assessment tools within the worksheets themselves.
How can I integrate technology with similarity worksheets?

+
Use apps or online tools that allow for resizing, scaling, or measuring of shapes. Digital worksheets or interactive quizzes can also engage students through gamification.
What strategies can be employed to help struggling students with similarity?

+
Provide visual aids, real-life examples, hands-on activities, and allow for more time on practice problems. Tailor explanations to their learning style, emphasizing diagrams and concrete examples.
Can you recommend activities that promote the understanding of similarity?
+
Consider activities like resizing buildings using scale factors, mapping projects, or even creating ‘giant-sized’ versions of everyday objects.