5 Must-Know Tips for Mastering Similar Triangles Proofs

Similar triangles form a fundamental concept in geometry, where understanding their properties can unlock the mysteries of scale, proportion, and symmetry in real-world applications. Whether you're delving into architecture, engineering, or any field that requires understanding spatial relationships, mastering the proofs of similar triangles can significantly enhance your problem-solving skills. Here are five essential tips to make you proficient in proving similarity in triangles:
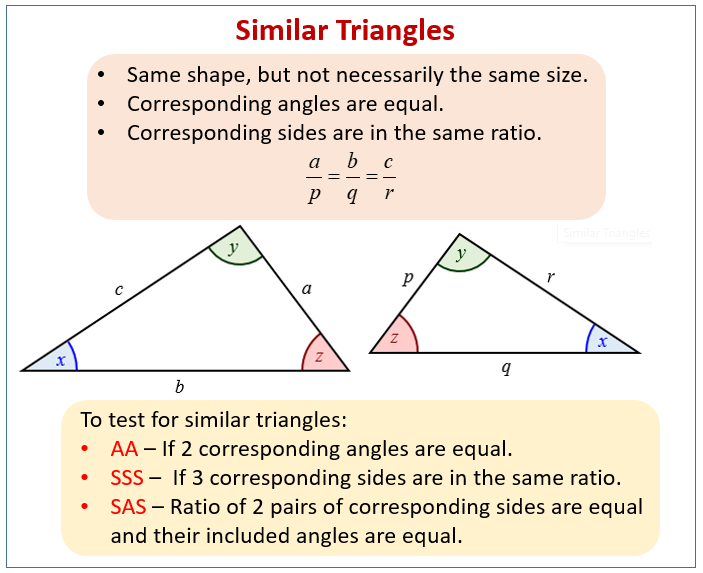
Tip 1: Grasp the Similarity Postulates

The foundation of proving similar triangles lies in three main postulates:
- Angle-Angle (AA) Similarity Postulate: If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
- Side-Angle-Side (SAS) Similarity Postulate: If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar.
- Side-Side-Side (SSS) Similarity Theorem: If corresponding sides of two triangles are proportional, then the triangles are similar.

📝 Note: Although these postulates are sufficient for proving similarity, understanding each has its own proof can help in advanced problem-solving.
Tip 2: Use Proportionality to Your Advantage

Proportions are the backbone of similarity. If you can establish that the corresponding sides of two triangles are proportional, you’re on your way to proving similarity. Here’s how to approach it:
- Set Up Proportions: Look for corresponding sides of the triangles you want to prove similar. Ensure these sides form ratios that are equal.
- Check Angles: If proportions are met, then verify the angles. One angle congruence is often enough with the AA postulate.
| Triangle ABC | Triangle DEF | Proportion |
|---|---|---|
| AB | DE | AB/DE = k |
| BC | EF | BC/EF = k |
| AC | DF | AC/DF = k |

🔍 Note: Proportions can be verified using cross-multiplication. If the cross-products are equal, the sides are proportional.
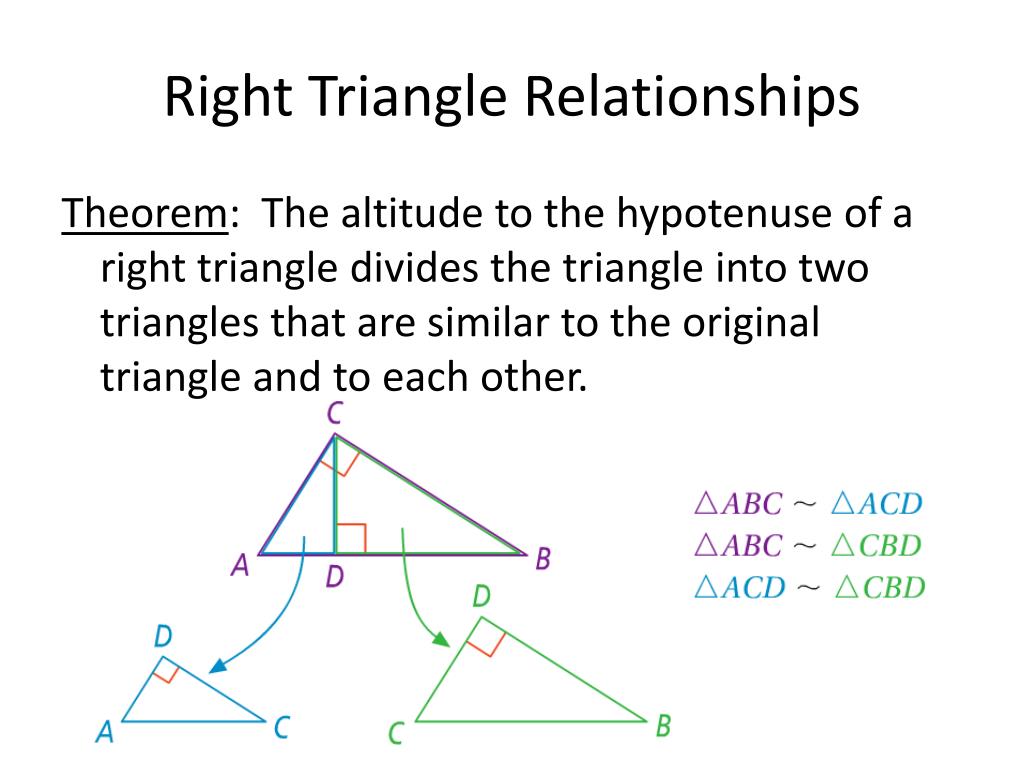
Tip 3: Recognize and Utilize Corresponding Angles

Corresponding angles are often key to quickly establishing similarity. Here’s what to look for:
- Angles Formed by Intersecting Lines: When two lines are cut by a transversal, the corresponding angles formed are equal.
- Parallel Lines: If a line intersects parallel lines, corresponding angles are congruent.
- Vertical Angles: Vertical angles are always congruent and can be used to show corresponding angle congruence in triangle proofs.
💡 Note: Paying attention to angles can sometimes provide a shortcut in proving similarity when sides are not directly given.
Tip 4: Be Mindful of the Pitfalls in Proofs
While proving triangle similarity, common mistakes can lead to incorrect conclusions:
- Assuming Similarity: Never assume triangles are similar without proof or evidence.
- Misapplication of Postulates: Ensure you’re applying the correct postulate or theorem for the scenario.
- Overlooking Scale Factors: The ratio between corresponding sides should be consistent; a slip in scale factor can invalidate the proof.
Tip 5: Practice and Visualize
Like any skill, mastering similar triangles proofs requires practice. Here are some techniques to enhance your practice:
- Draw Diagrams: Visualization is crucial. Always draw accurate diagrams to understand how angles and sides relate.
- Explore Real-Life Examples: From photography to structural engineering, real-life examples help reinforce theoretical knowledge.
- Use Software Tools: Geometric software can allow you to manipulate shapes and explore similarity dynamically.
- Work on Past Exam Problems: Exam problems provide insight into common pitfalls and standard question formats.
🔧 Note: Drawing is not just for visualization; it’s also a tool for spotting errors in your reasoning.
In summary, to excel in proving the similarity of triangles, you must comprehend the core postulates, recognize and utilize corresponding angles, and avoid common pitfalls through careful attention to detail. Regular practice, especially with visual aids and real-life applications, will help cement these concepts in your mind, allowing you to tackle complex geometry problems with ease.
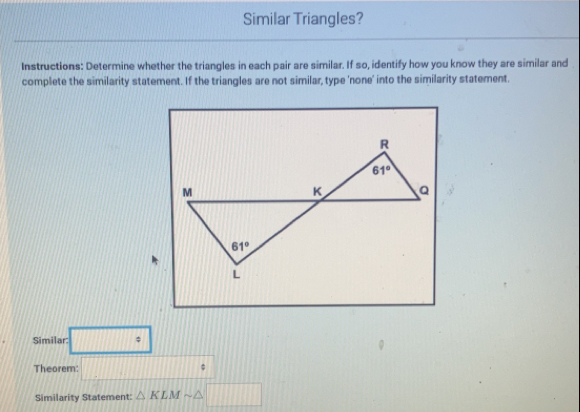
What are the basic rules for similar triangles?
+
The basic rules for proving similar triangles are the AA (Angle-Angle), SAS (Side-Angle-Side), and SSS (Side-Side-Side) similarity postulates.
How do I ensure I’m using the correct postulate in a proof?

+
Start by identifying what information you’re given in the problem. If you have two congruent angles, use AA; if you have two sides proportional with an included angle, use SAS; for all sides proportional, SSS is your choice.
Can similar triangles have different areas?

+
Yes, similar triangles can have different areas. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.


