Finding Missing Sides in Similar Triangles Worksheet
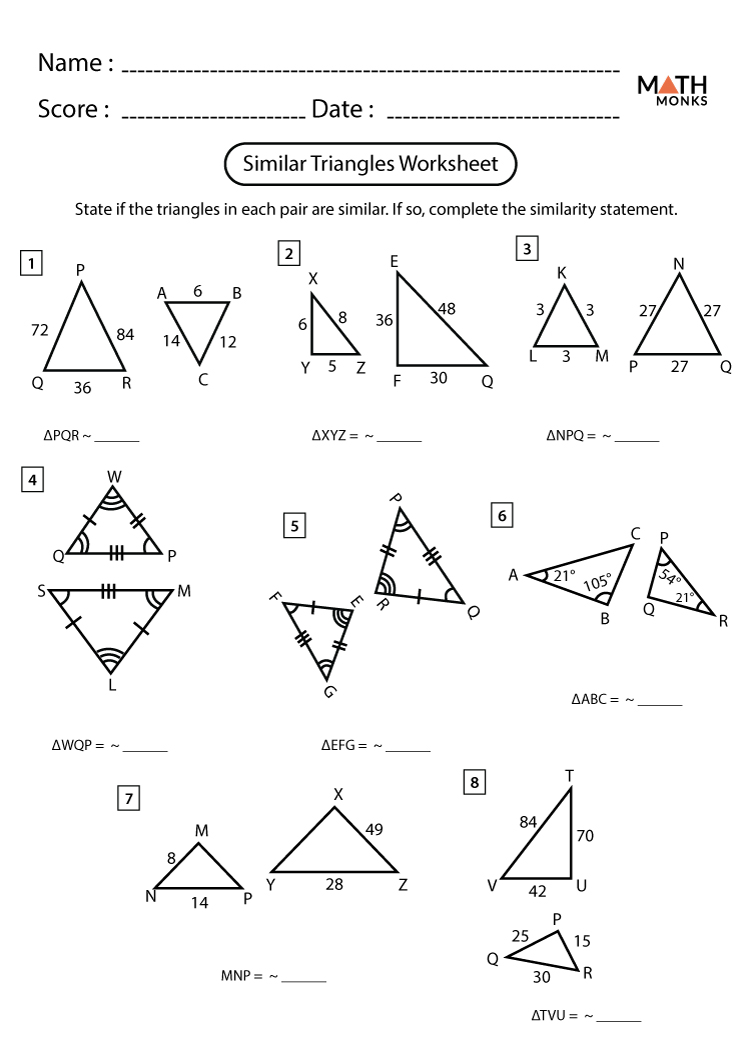
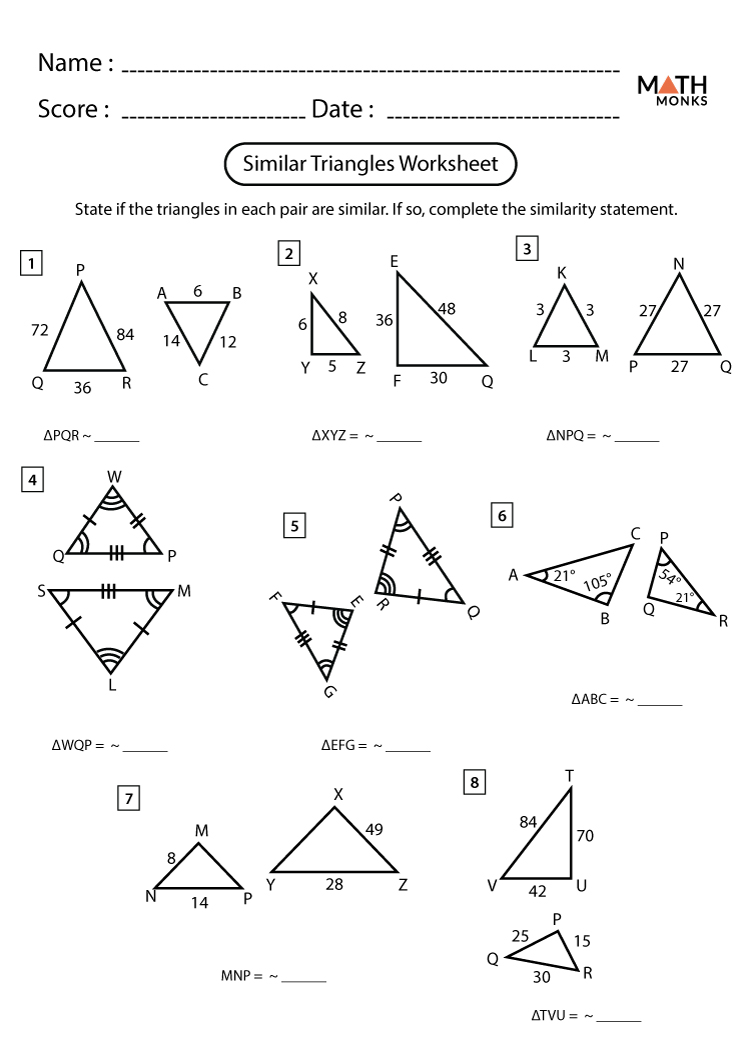
Discovering How to Find Missing Sides in Similar Triangles
When delving into the realm of geometry, one of the most fascinating and useful concepts is the study of similar triangles. These triangles, which share identical angles but differ in size, offer a unique opportunity to uncover relationships between their corresponding sides. This ability to identify and work with similar triangles can simplify many geometric problems, particularly when it comes to finding missing sides.
Understanding Similar Triangles

Before diving into methods of finding missing sides, it's essential to understand what makes triangles similar:
- All corresponding angles are equal.
- The ratio of corresponding side lengths is consistent (the triangles are proportional).
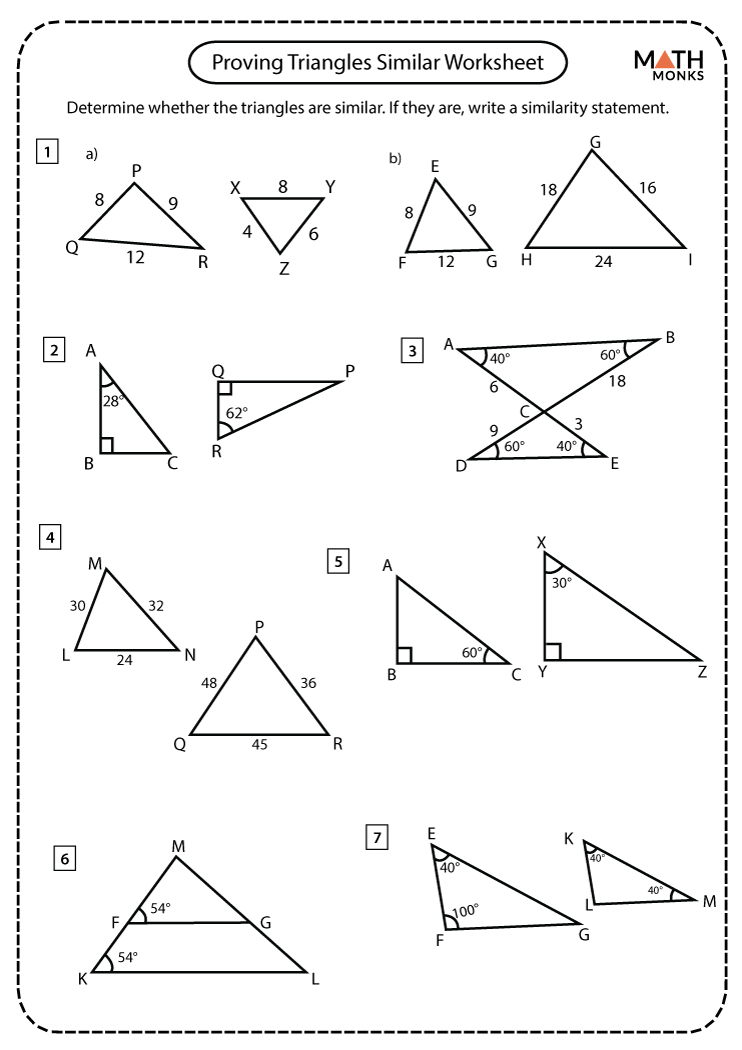
Finding Missing Sides
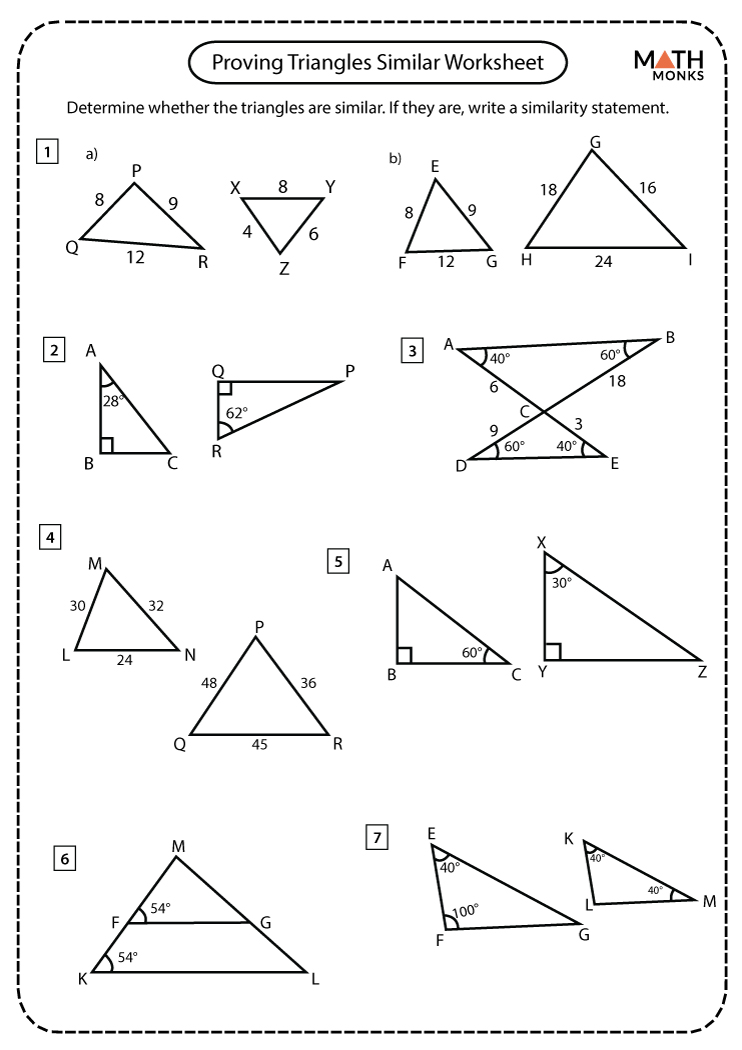
The primary tool for finding missing sides in similar triangles is the concept of proportions. Here's how you can approach this:
1. Identifying Corresponding Sides
The first step is to identify which sides correspond to one another in the similar triangles. This can be done by:
- Comparing angles: Sides opposite the same angles in similar triangles are corresponding.
- Using notation: Often, triangles are labeled with letters, making it easier to match sides.
2. Setting Up the Proportion
Once you've identified the corresponding sides, set up a proportion:
[ \frac{\text{Length of side 1 in Triangle 1}}{\text{Length of side 2 in Triangle 1}} = \frac{\text{Corresponding side 1 in Triangle 2}}{\text{Corresponding side 2 in Triangle 2}} ]
Let's denote the triangles as \triangle ABC \sim \triangle DEF where AB corresponds to DE, BC corresponds to EF, and AC corresponds to DF. If we want to find the length of AC when we know AB = 3, BC = 4, DE = 6, and EF = 8, the proportion would look like this:
[ \frac{3}{4} = \frac{6}{8} = \frac{x}{10} ]
3. Solving for the Unknown
Now, solve for x using cross-multiplication:
[ 3 \times 8 = 4 \times x ] [ 24 = 4x ] [ x = \frac{24}{4} ] [ x = 6 ]
4. Check Your Work
Ensure your calculations are correct by comparing the ratios of the other sides. If all ratios hold true, your solution is likely correct.
⚠️ Note: Always verify your answers by checking the ratios of the other sides, ensuring all are consistent with the similarity ratio.
Example Worksheet
| Problem | Given | Proportion | Solution |
|---|---|---|---|
| 1 | \triangle ABC \sim \triangle DEF, AB = 4, BC = 6, DE = 8, EF = ? | \frac{4}{6} = \frac{8}{EF} | EF = 12 |
| 2 | \triangle PQR \sim \triangle XYZ, PQ = 5, PR = 7, XY = 10, XZ = ? | \frac{5}{7} = \frac{10}{XZ} | XZ = 14 |
| 3 | \triangle KLM \sim \triangle RST, KL = 9, LM = 12, RS = 6, RT = ? | \frac{9}{12} = \frac{6}{RT} | RT = 8 |
Real-Life Applications

Understanding how to find missing sides in similar triangles has practical applications in various fields:
- Architecture: Ensuring structural integrity and design accuracy in buildings.
- Surveying: Calculating distances where direct measurement is not feasible.
- Photography: Adjusting lens focal lengths to maintain perspective and achieve desired compositions.
To wrap up, similar triangles offer a powerful method for simplifying geometric problems. By identifying corresponding sides and setting up and solving proportions, you can easily find missing sides. This knowledge is not only useful in theoretical problems but also has practical applications in various fields. Continuously practicing with worksheets and real-world scenarios will help solidify this understanding.
What are the main properties of similar triangles?

+
The main properties of similar triangles include having corresponding angles that are equal and having the lengths of corresponding sides in proportion.
How do you set up a proportion when finding missing sides?

+
You set up a proportion by comparing the lengths of corresponding sides between the two triangles. For example, (\frac{AB}{BC} = \frac{DE}{EF}) where (AB) corresponds to (DE) and (BC) corresponds to (EF).
Why is it useful to know how to find missing sides in similar triangles?

+
This knowledge is crucial for solving geometric problems, indirect measurement in surveying, scaling objects in design and architecture, and adjusting perspectives in photography.