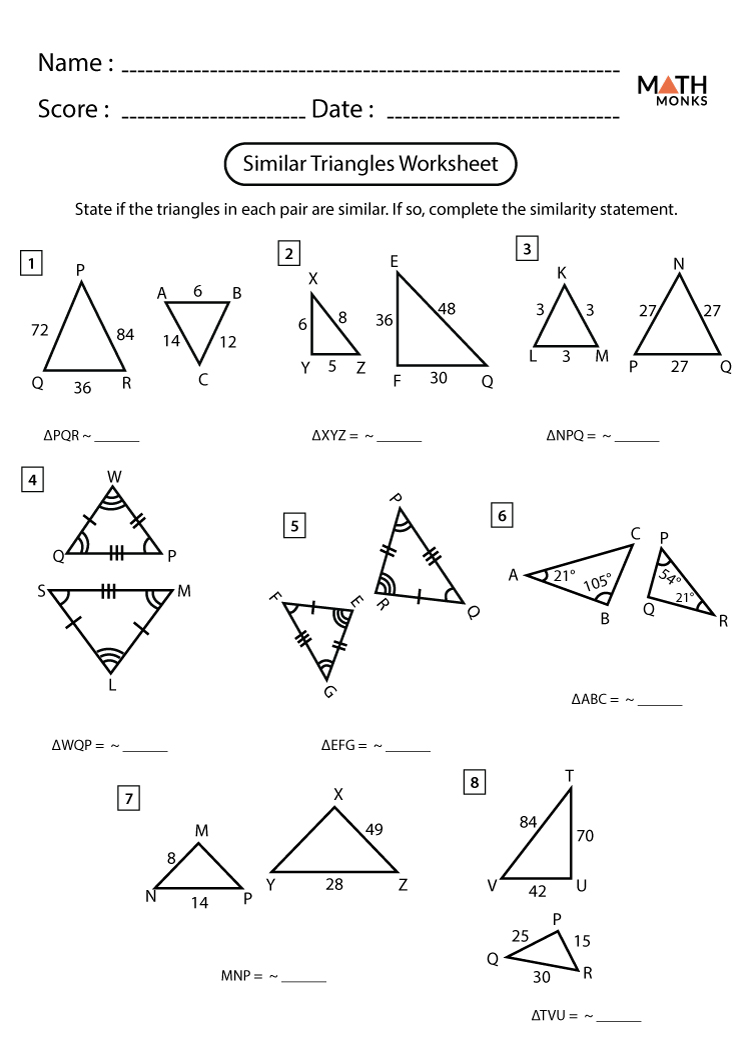
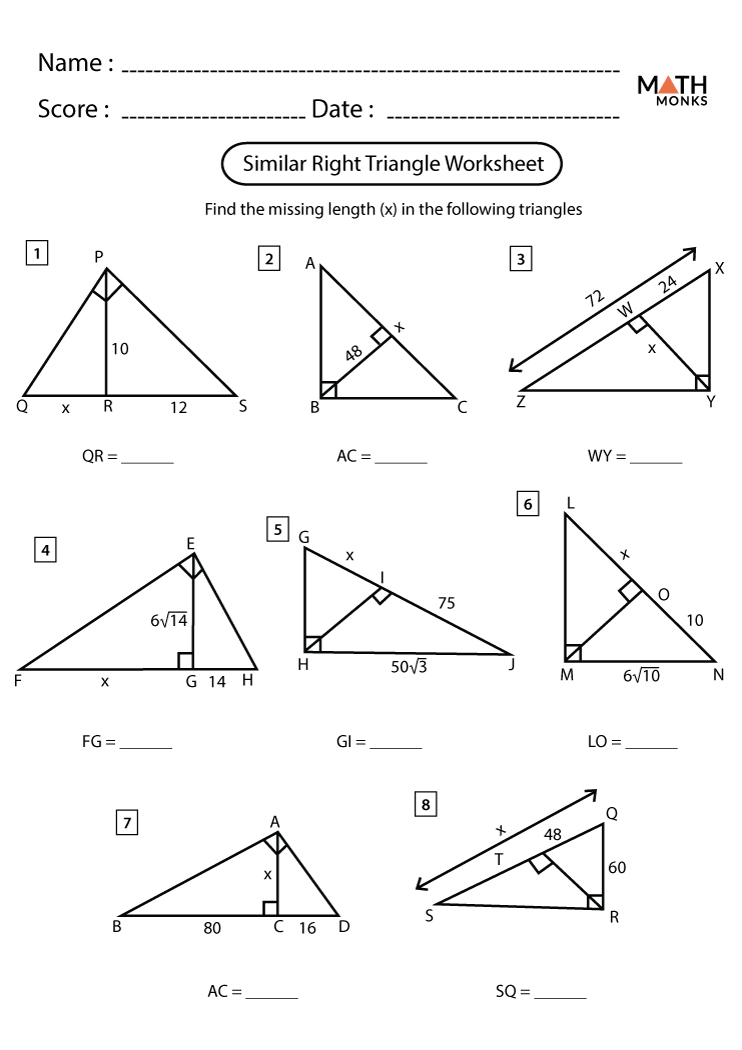
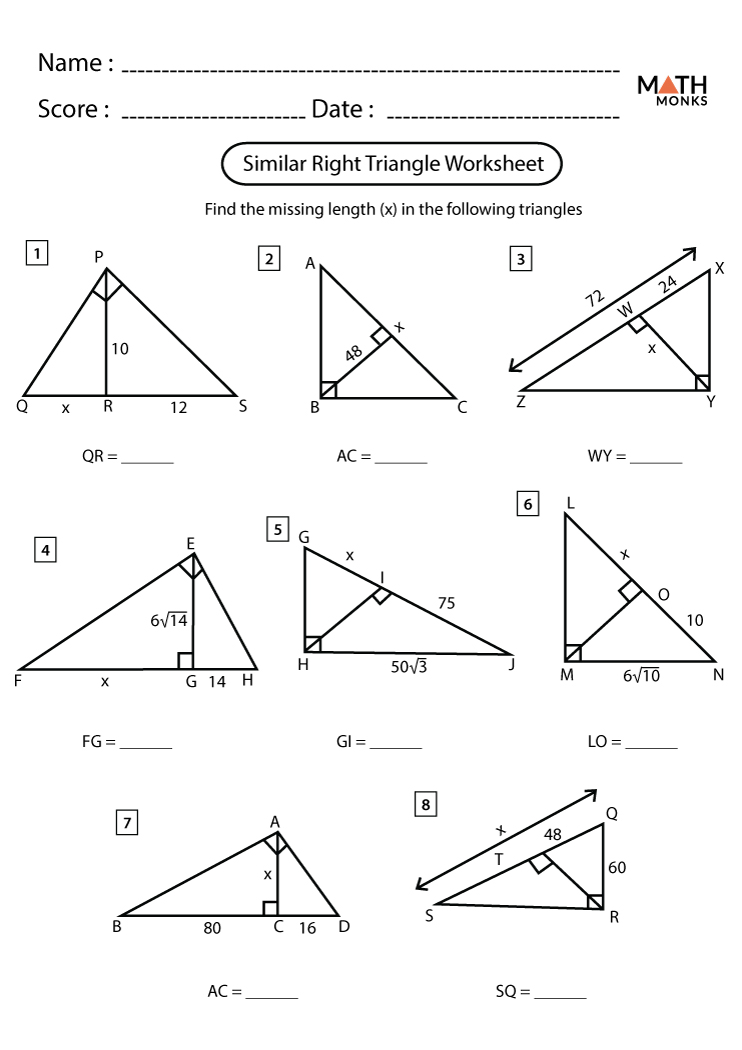
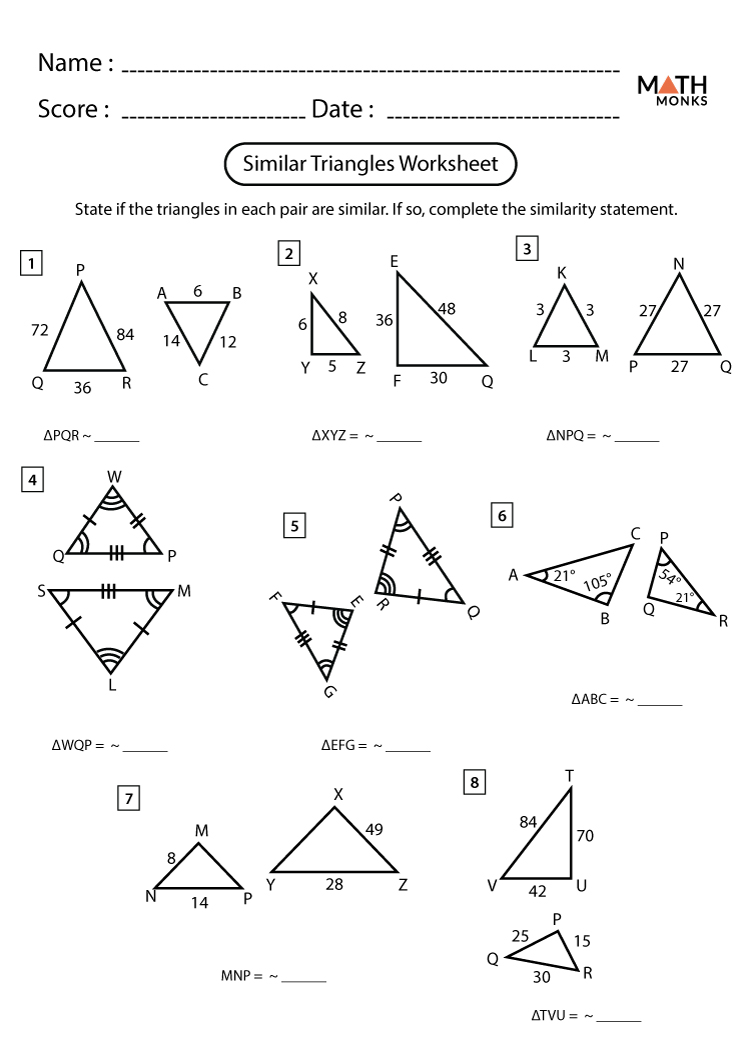
Similar Triangles Worksheet Answers: Real-World Applications
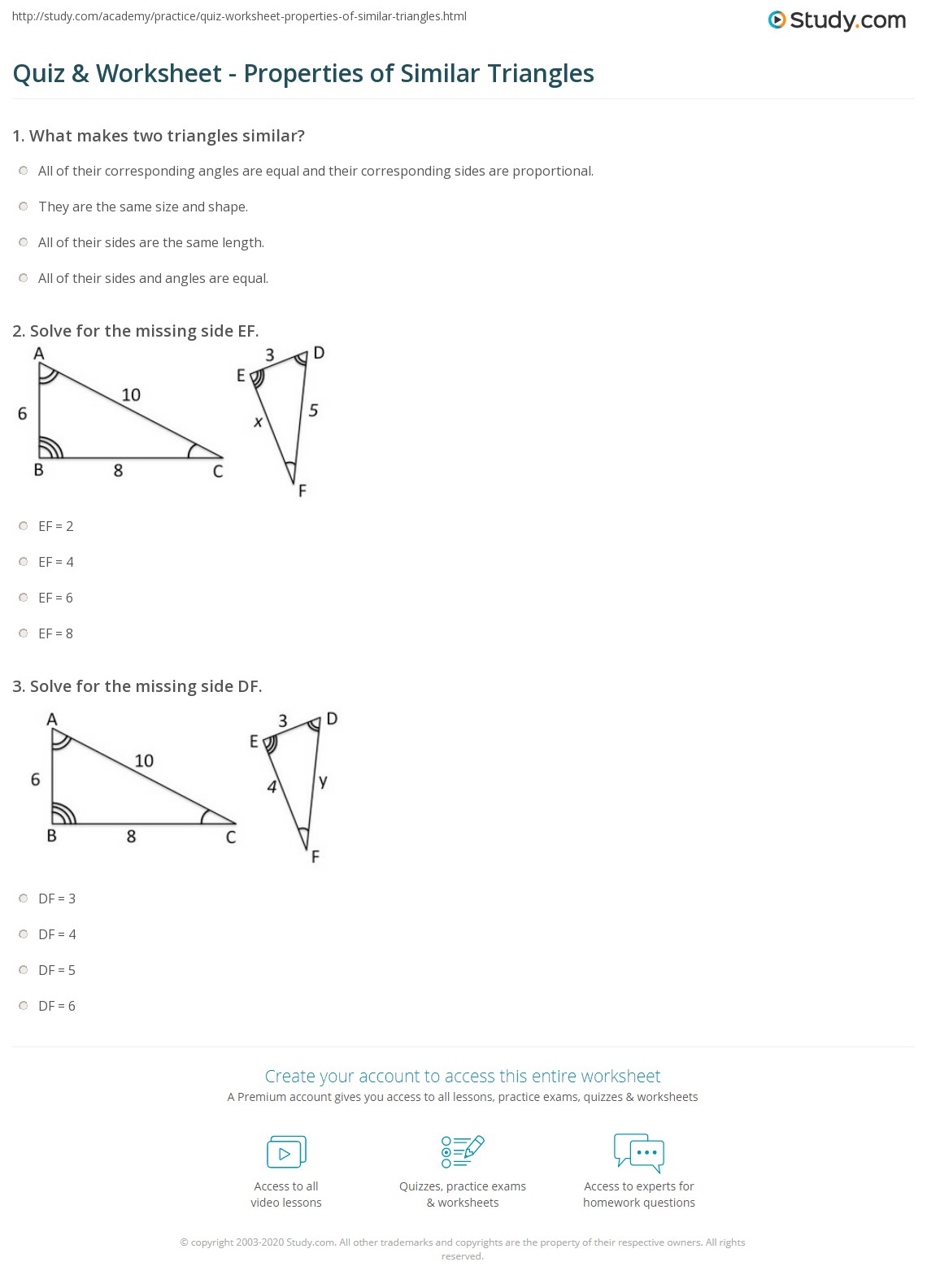
In the realm of geometry, the concept of similar triangles is not just an abstract mathematical idea but has real-world applications that enhance our understanding and interaction with our environment. This blog post delves into how this mathematical concept is applied in various fields, from architecture to art, and provides solutions to common problems found in similar triangles worksheets to help you grasp these applications more effectively.
Applications in Architecture

Architecture heavily relies on the principles of geometry for design and construction. Here’s how similar triangles play a role:
- Shadow Projections: Architects use the concept of similar triangles to predict how long shadows will be cast by buildings at different times of the day or year. This information helps in planning outdoor spaces and avoiding long shadows in certain areas.
- Building Proportions: The golden ratio, often found in the design of buildings, uses similar triangles to achieve aesthetically pleasing proportions. For example, the ratio between the sides of triangles in a building’s facade can be designed to mimic the natural proportions found in nature.
- Scale Models: Architects create scale models of buildings. Using similar triangles ensures that the dimensions of the model reflect accurately the full-scale building. If the model’s height is 10 times less than the actual building, then all other corresponding lengths must also be 10 times smaller for the model to be truly similar.
Solutions to Similar Triangles Problems

| Problem | Solution |
|---|---|
| Given two triangles, ABC and DEF, with AB = 4cm, BC = 6cm, DE = 6cm, and DF = 9cm. Determine if these triangles are similar. | Since the ratio of corresponding sides AB:DE (4:6 or 2:3) matches BC:DF (6:9 or 2:3), by the Ratio Test, triangles ABC and DEF are similar. |
| Find the length of a missing side in a triangle similar to one where AC = 8cm, CB = 5cm, and the corresponding side in the other triangle is known to be 10cm for CA’ | Using the ratio of similarity, since CA’:AC = 10:8, the unknown side CB’ can be found by multiplying 5cm by the ratio, which equals 6.25cm. |
Applications in Photography
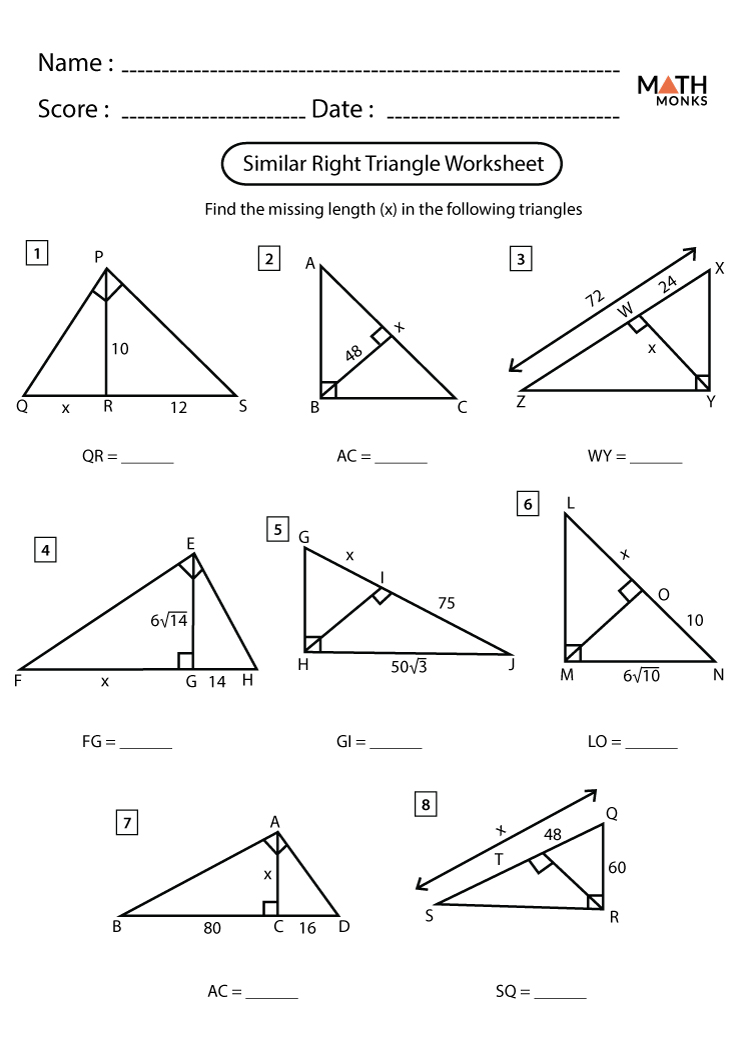

Photographers utilize the principles of similar triangles to capture perfect angles and perspectives:
- Field of View: The angle of the lens to the subject and the subject to the ground forms similar triangles, which helps photographers understand how to frame their shots for desired effects.
- Depth Perception: In wide-angle photography, understanding similar triangles aids in creating a sense of depth. A photographer can use the known heights of objects to estimate distances and ensure foreground and background elements are appropriately proportioned.
- Perspective Control: Photographers use tilt-shift lenses to manipulate perspective. By knowing the properties of similar triangles, they can correct lens distortions and ensure parallel lines remain parallel in the image.
📷 Note: Similar triangles are also crucial in creating special effects like miniature fakes through forced perspective photography, where large objects appear smaller due to angular alignment.
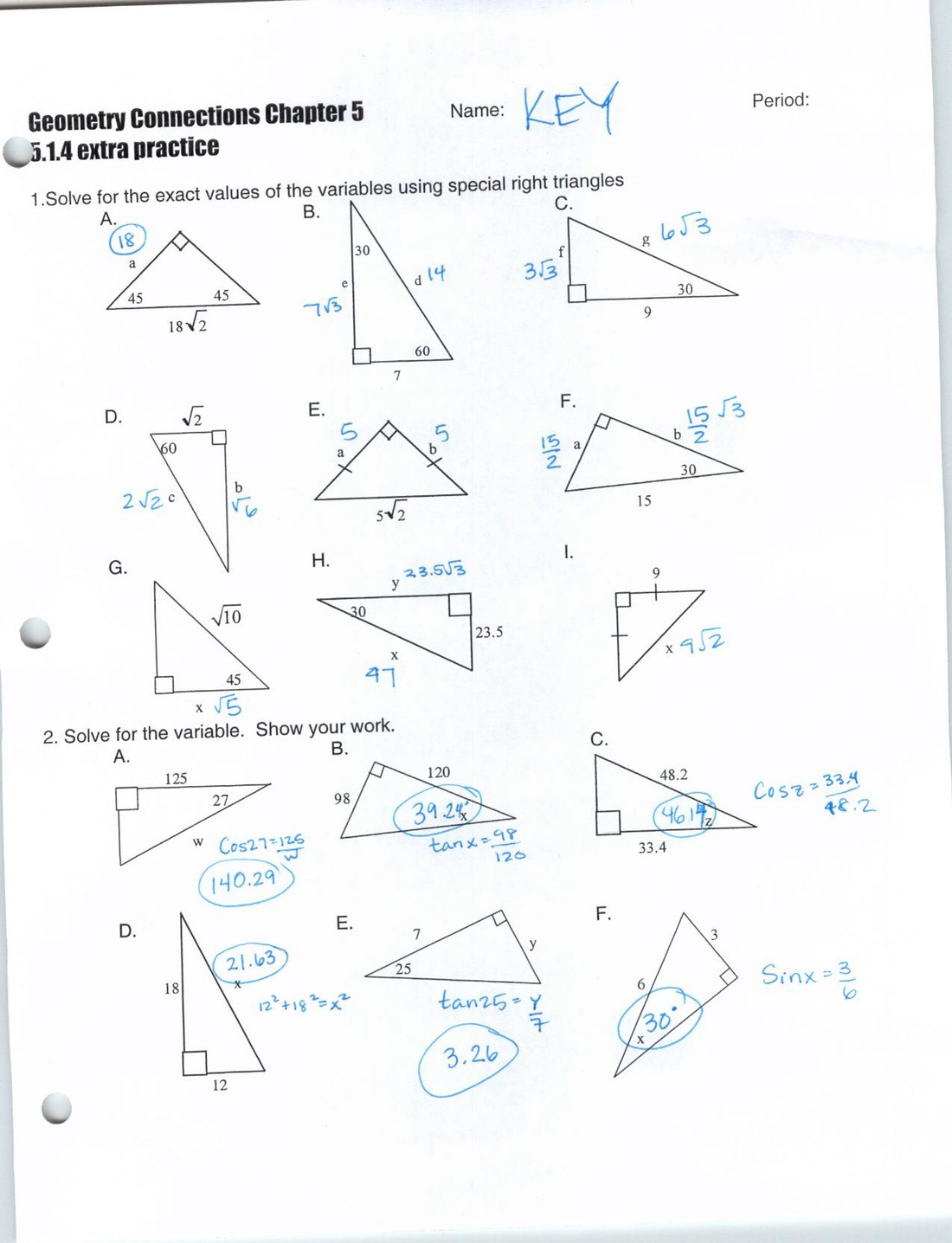
Applications in Engineering

In engineering, the principles of similar triangles are indispensable:
- Optical Engineering: Optics rely on the properties of similar triangles to design lenses and mirrors, ensuring light paths converge or diverge appropriately to form images or focus light.
- Mechanical Design: Machine parts are often designed in similar triangular patterns to ensure mechanical advantages and reduce stress concentration points.
- Force Analysis: Engineers calculate forces in structures by analyzing force diagrams where similar triangles often appear, allowing for stress calculations based on the proportionality of force vectors.
Art and Perspective Drawing


The use of perspective in art to create depth and realism is directly linked to the study of similar triangles:
- Vanishing Points: When drawing in one-point or two-point perspective, the rules of similar triangles help artists locate vanishing points and ensure that objects diminish in size correctly as they recede.
- Size and Distance: Artists use the known dimensions of an object to calculate the size of other objects at different distances, creating a realistic sense of depth.
- Shadows and Light: The fall of shadows and the angle of light sources are calculated using similar triangles, enabling artists to depict realistic shading.
In closing, the application of similar triangles extends far beyond the classroom worksheet. From designing skyscrapers to capturing breathtaking photographs, from engineering solutions to creating art, understanding this concept provides a fundamental tool for interpreting and influencing the world around us. By solving worksheet problems, you not only practice mathematical skills but also equip yourself to recognize and utilize these patterns in your daily life.
How do architects use similar triangles in building design?

+
Architects use similar triangles to ensure proportional designs, predict shadow lengths, and maintain aesthetic ratios in their structures.
Can similar triangles be applied to photography?
+
Yes, photographers use similar triangles for framing shots, creating forced perspectives, and controlling depth perception in wide-angle photography.
Why are similar triangles important in engineering?
+
Engineers use similar triangles for optical design, mechanical stress analysis, and calculating force distribution in structures.