5 Ways Semicircle Center Mass

Understanding the Concept of Semicircle Center Mass

The concept of center mass, especially in the context of a semicircle, is crucial in geometry and physics. It refers to the point where the entire mass of an object can be considered to be concentrated for the purpose of analyzing its motion or balance. For a semicircle, finding the center of mass involves understanding its geometric properties and applying principles of physics. In this article, we will explore five ways to approach the concept of semicircle center mass, making it easier to grasp and apply in various scenarios.

1. Geometric Approach

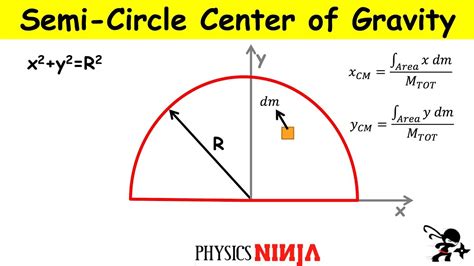
From a geometric standpoint, the center of mass of a semicircle can be determined by considering its symmetry. The semicircle is symmetric about its diameter. Thus, the center of mass lies on the diameter, at a distance from the midpoint of the diameter that depends on the density distribution of the semicircle. For a uniform semicircle, this point can be calculated using geometric formulas. Specifically, for a semicircle of radius (r), the center of mass is located at a distance of (\frac{4r}{3\pi}) from the midpoint of the diameter, along the diameter and towards the center of the circle from which the semicircle is derived.

2. Physical Approach

Physically, the center of mass of an object is the point where the weight of the object can be considered to act. For a semicircle, if it were a physical object with uniform density, the center of mass would be the point where the semicircle would balance if placed on a single point support. This approach involves understanding the physical properties of the semicircle, such as its mass distribution and how it responds to forces like gravity. By considering the semicircle as part of a full circle and then removing the upper half, one can intuitively understand how the center of mass shifts downwards from the center of the full circle.

3. Mathematical Derivation

Mathematically, the center of mass of a semicircle can be derived by integrating the infinitesimal areas of the semicircle and their respective distances from a chosen axis. This involves calculus, specifically integration, to sum up the moments of these infinitesimal areas about the axis. The formula for the center of mass (x{cm}) of a semicircle of radius (r) is given by: [x{cm} = \frac{\int{0}^{r} x \cdot \rho \cdot \pi \cdot \sqrt{r^2 - x^2} dx}{\int{0}^{r} \rho \cdot \pi \cdot \sqrt{r^2 - x^2} dx}] where (\rho) is the density of the semicircle. Simplifying this expression yields the distance of the center of mass from the midpoint of the diameter.

4. Comparison with Other Shapes

Comparing the center of mass of a semicircle with that of other geometric shapes can provide insight into its unique properties. For instance, the center of mass of a full circle is at its geometric center, while that of a rectangle is at the intersection of its diagonals. By comparing these, one can see how the removal of half the circle shifts the center of mass downwards. This comparative approach helps in understanding the geometric and physical factors that influence the center of mass.

5. Practical Applications

Lastly, understanding the center of mass of a semicircle has practical applications in engineering and design. For example, in the construction of arches or in the design of mechanical components, knowing the center of mass can help in determining the stability and balance of the structure or component. It’s also crucial in dynamics, where the motion of objects is analyzed around their center of mass.

📝 Note: The calculation and understanding of the center of mass are fundamental in both statics and dynamics, and applying these principles can significantly affect the performance and safety of designs and structures.

In summary, the concept of semicircle center mass is multifaceted and can be approached from geometric, physical, mathematical, comparative, and practical standpoints. Each of these approaches offers a unique perspective on how the center of mass is determined and its significance in various fields. By grasping these concepts, one can better understand and apply the principles of physics and geometry to solve problems and design structures and mechanisms effectively.