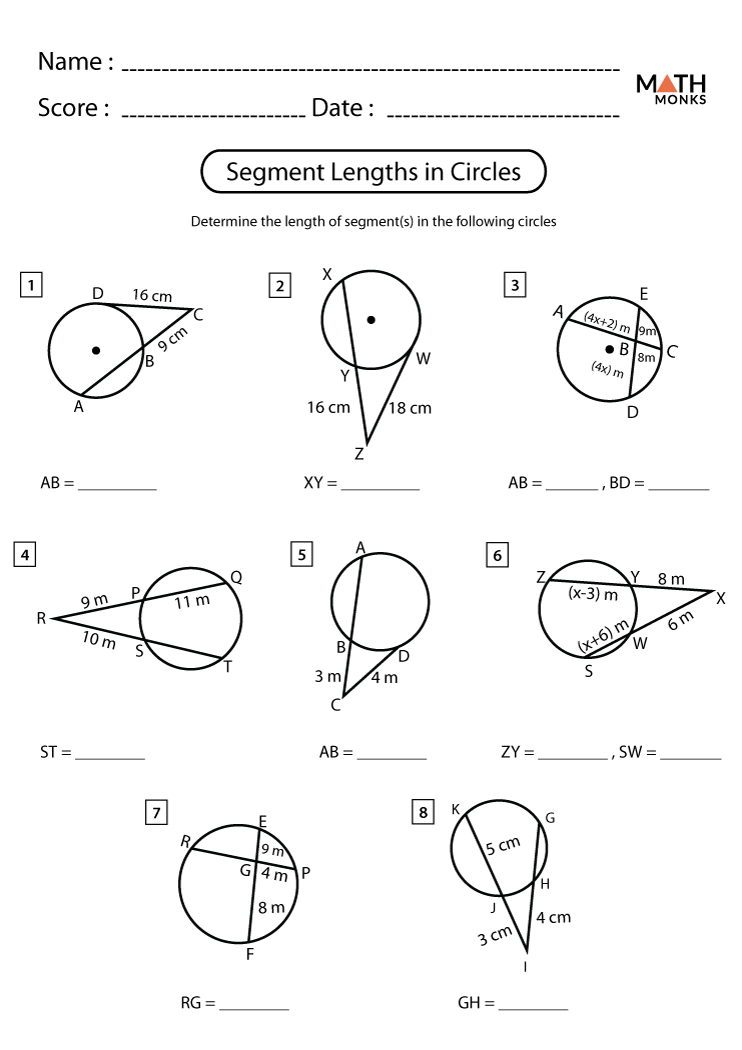
Segment Relationships in Circles: Worksheet Guide

In the world of geometry, understanding segment relationships in circles is crucial for not only advanced mathematics but also for practical applications in various fields such as engineering, architecture, and design. This guide provides a comprehensive walkthrough for students and enthusiasts on how to navigate and solve problems related to segment relationships in circles. We'll explore definitions, theorems, properties, and practical examples, ensuring you have a solid grasp on this fascinating aspect of geometry.
Understanding Circle Segments

Circles, with their simple yet profound nature, offer a playground for numerous geometric principles. A segment in a circle is the region bounded by a chord and the arc it subtends. Here's a quick overview:
- Chord: A straight line segment whose endpoints lie on the circumference of the circle.
- Arc: A portion of the circle's circumference.
- Major and Minor Segments: A chord divides the circle into two segments. The larger part is the major segment, and the smaller part is the minor segment.
To illustrate, let's imagine a circle with a chord from point A to point B. The part of the circle above the chord would be the major segment, while the part below would be the minor segment.
Key Theorems and Properties

To solve problems related to segments in circles, you need to understand several key theorems and properties:
Angle at the Circumference Theorem

The angle formed at the circumference of a circle by a chord and its tangent is equal to the angle subtended by the chord in the alternate segment:
- The angle at the circumference theorem states that the angle formed at the circumference by any chord with any point on the circumference is half the central angle subtended by the same chord.
- The angle between the tangent and the chord through the point of contact is equal to the angle in the alternate segment (opposite).
Chord Bisector Theorem
This theorem states:
- If a line segment bisects a chord in a circle, it is perpendicular to the chord and passes through the circle's center.
Steps to Solve Segment Problems

Let's walk through a typical problem involving segment relationships:
Problem:

Given a circle with center O, point A on the circle and chord AB. If angle ACB (where C is a point on the circle) is 35 degrees, find the angle BOC.
Solution Steps:

- Identify the theorem: Use the angle at the circumference theorem. Angle ACB is half the central angle BOC.
- Set up the equation: \[ \text{Angle ACB} = \frac{1}{2} \times \text{Angle BOC} \] \[ 35^\circ = \frac{1}{2} \times \text{Angle BOC} \]
- Solve for the angle: \[ \text{Angle BOC} = 35^\circ \times 2 = 70^\circ \]
💡 Note: Always verify your solutions by checking the principles and theorems applied. Geometry often involves visual reasoning alongside algebraic computation.
Common Pitfalls and Tips

- Be cautious with the signs and the placement of angles.
- Remember, angles in the same segment are equal, but angles at the circumference subtended by the same chord are equal only in the same segment.
- Use constructions or sketches to help visualize the problem. Sometimes, adding auxiliary lines or points can simplify a complex problem.
Practical Applications
Understanding segment relationships isn't just for academic purposes; here are some real-world applications:
Architecture and Engineering:
- Designing arches or structural elements where circular shapes are prominent.
Computer Graphics:

- Calculating curves and segments for rendering circles or arcs in 2D or 3D modeling.
Navigation and Cartography:

- Understanding spherical geometry to navigate on Earth or to map out territories.
The study of segment relationships in circles blends mathematical logic with practical problem-solving, enhancing not only your mathematical skills but also your ability to apply these concepts in real-world scenarios.
By understanding these relationships, you are equipped to tackle more advanced geometric problems, dive into higher mathematics, and explore a wide range of applications from art to engineering. This guide serves as a stepping stone towards mastering these essential geometric concepts.
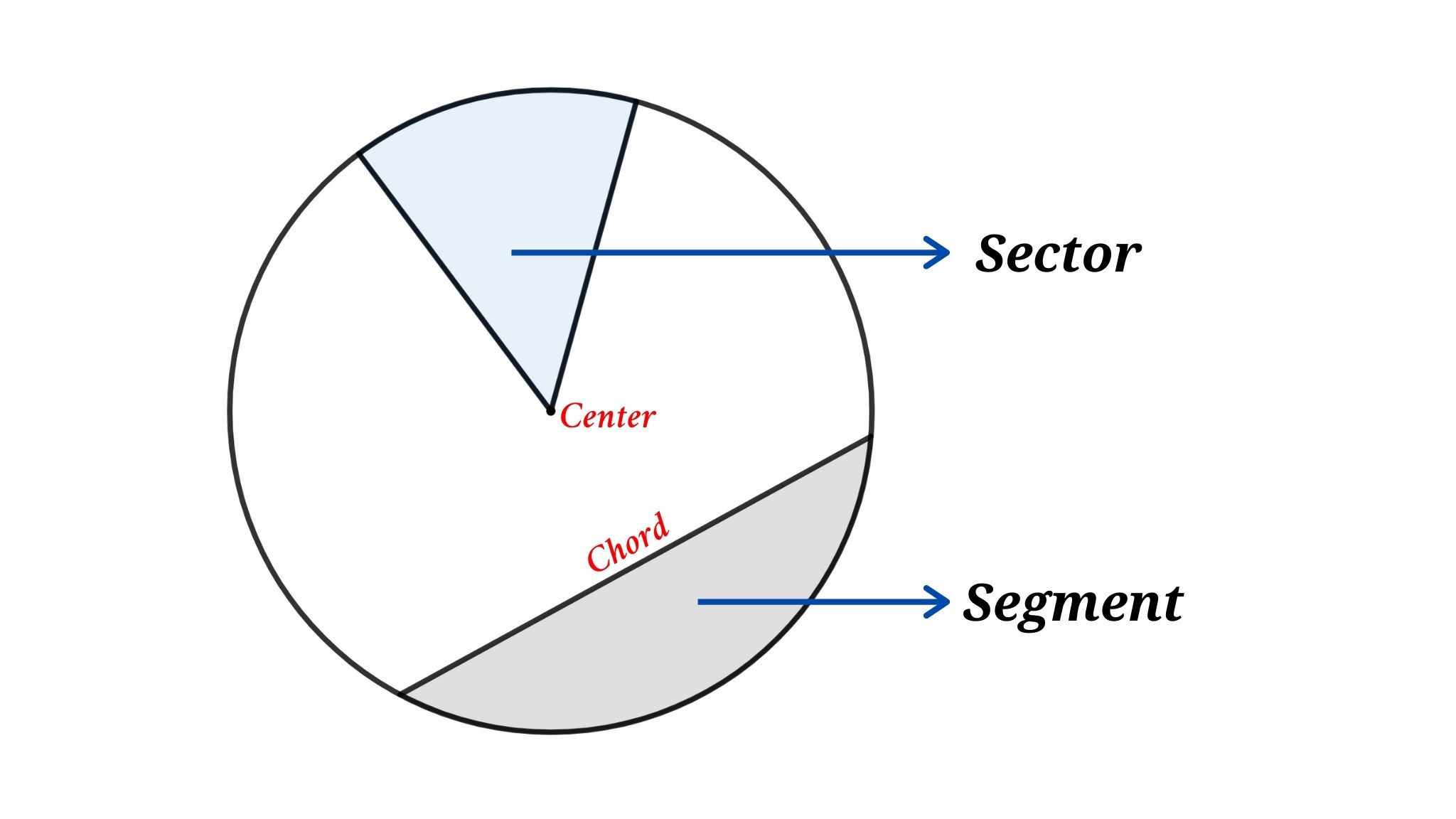
What is the difference between a sector and a segment of a circle?
+
A sector is the portion of the circle between two radii and the arc enclosed by them, including the radii. A segment, on the other hand, is the region bounded by an arc and the chord joining the arc’s endpoints, excluding the arc but including the chord.
How can I find the area of a segment of a circle?

+
To find the area of a segment, subtract the area of the triangle formed by the chord and the radii from the area of the sector:
[ \text{Area of Segment} = \text{Area of Sector} - \text{Area of Triangle} ] Where: [ \text{Area of Sector} = \frac{\theta}{360} \times \pi r^2 ] [ \text{Area of Triangle} = \frac{1}{2} \times r \times r \times \sin(\theta) ] Here, ( \theta ) is the central angle in degrees, and ( r ) is the radius of the circle.
Why is the angle at the circumference theorem useful?

+
The angle at the circumference theorem simplifies many calculations by relating angles on the circumference to angles at the center of the circle. This theorem is particularly useful in problems where the angle subtended by a chord at the center needs to be found or when the chord’s length or the circle’s radius is given.