Discover Answers to Segment Lengths in Circles Worksheet
Segment lengths in circles are a fundamental concept in geometry that often appears in various forms in textbooks, exams, and real-world applications. Understanding how to calculate these lengths not only enhances your geometric knowledge but also opens doors to solving complex mathematical problems involving circles. In this comprehensive guide, we'll dive deep into the methods and strategies for finding segment lengths, with particular emphasis on the segments created by chords, tangents, and secants.
What Are Chords, Secants, and Tangents?

Before we delve into calculating segment lengths, let’s define the key players in a circle:
- Chord: A straight line segment whose endpoints lie on the circle. The diameter is the longest possible chord.
- Secant: A line that intersects a circle at exactly two points. It contains the chord that connects these points.
- Tangent: A line that touches the circle at exactly one point, called the point of tangency. It doesn’t enter the interior of the circle.
Segment Lengths in Circles: The Rules

When dealing with segments in circles, three main scenarios arise:
- Two Secants Theorem: If two secants are drawn from an external point to a circle, then the product of the lengths of the external segment and the entire secant is equal for both secants.
- Secant-Tangent Theorem: When a secant and a tangent are drawn from an external point to a circle, the square of the length of the tangent segment is equal to the product of the lengths of the external segment and the entire secant.
- Intersecting Chords Theorem: If two chords intersect inside a circle, the products of their segments are equal.
Calculating Segment Lengths: Practical Examples

Let’s work through some practical examples to illustrate how these rules apply:
Example 1: Two Secants

Given two secants AB and CD, where A and B lie outside the circle, and C and D are points of intersection:
- Let the external segment AB be 15 cm.
- Let the entire secant length of AB be 30 cm.
- Let CD intersect the circle at points C and D such that the segment outside the circle is 8 cm.
We can find the length of CD using the Two Secants Theorem:
15 × 30 = 8 × CD
CD = (15 × 30) / 8 = 56.25 cm
Therefore, the secant CD is 56.25 cm long.
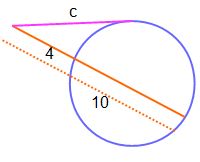
Example 2: Secant-Tangent

Given a secant AB and a tangent BC, where A lies outside the circle, and C is the point of tangency:
- Let the external segment of secant AB be 12 cm.
- Let the entire secant length of AB be 20 cm.
- Find the length of the tangent BC:
Using the Secant-Tangent Theorem:
BC² = 12 × 20
BC² = 240
BC = √240 ≈ 15.49 cm
Example 3: Intersecting Chords

Given two chords AB and CD intersecting at point E:
- Let AE = 4 cm and EB = 6 cm.
- Let CE = 3 cm.
- Find the length of ED:
Using the Intersecting Chords Theorem:
AE × EB = CE × ED
4 × 6 = 3 × ED
ED = (4 × 6) / 3 = 8 cm
💡 Note: These theorems provide a structured approach to solving segment length problems in circles. Memorizing these rules can significantly expedite your problem-solving skills.
Visualizing Segment Lengths
| Theorem | Formula |
|---|---|
| Two Secants | EA × EB = EC × ED |
| Secant-Tangent | EC² = EA × (EA + EB) |
| Intersecting Chords | AE × EB = CE × ED |

Advanced Techniques for Segment Lengths

Here are some advanced techniques to consider:
- Use of Trigonometry: For intersecting chords at an angle, sine and cosine laws can be applied to find segment lengths.
- Construction Techniques: Using geometric constructions like drawing radii or perpendicular bisectors can help in finding unknown segments.
- Power of a Point: This theorem states that for any point, the power of the point with respect to a circle remains constant for any pair of intersecting chords, secants, or tangent-secant pairs.
🔍 Note: Understanding the power of a point concept can be crucial for solving non-standard problems or when direct application of simple segment theorems is not feasible.
Common Mistakes to Avoid

When calculating segment lengths:
- Ensure correct application of theorems; don’t confuse secants with tangents.
- Be mindful of the correct identification of external and internal segments.
- Avoid assumptions about equal lengths when segments look the same in diagrams.
- Double-check measurements and calculations, as small errors can lead to incorrect results.
To conclude, mastering segment lengths in circles is not just about knowing formulas but also understanding the relationships between different parts of a circle. By applying the theorems for two secants, secant-tangent, and intersecting chords, along with visualizing these segments through diagrams and tables, you can solve an array of circle problems efficiently. This knowledge is invaluable not only for academic purposes but also in fields like architecture, engineering, and design, where understanding circular geometry can be a practical asset.
What is the difference between a secant and a tangent?

+
A secant intersects a circle at two points and extends inside the circle. In contrast, a tangent touches the circle at exactly one point and does not enter the circle’s interior.
How do I use trigonometry to find segment lengths in circles?

+
When chords or secants intersect at an angle, you can use the sine law or cosine law from trigonometry. For example, if the angle between two intersecting chords is known, you can use these laws to find unknown segment lengths.
Can I use the segment length theorems in real-world applications?

+
Absolutely! Engineers, architects, and designers often use these principles when dealing with curved structures or in computer-aided design (CAD) software for precise modeling.